sagnik242
Hi, I am reading the Math Book and taking notes.
I came across page 50 discussing the overlapping formulas and I came across this passage:
"Hence we need to subtract d,e, and f once (to count section g once) and subtract section g twice (again to count section g only once)
MY QUESTION : what exactly is the relation of d,e,and f to g? Also if we have already done the procedure to count section G only once, why do we have to do it again?
ADVANCED OVERLAPPING SETS PROBLEMSSome 700+ GMAT quantitative questions will require you to know and understand the formulas for set theory, presenting three sets and asking various questions about them. There are two main formulas to solve questions involving three overlapping sets. Consider the diagram below:
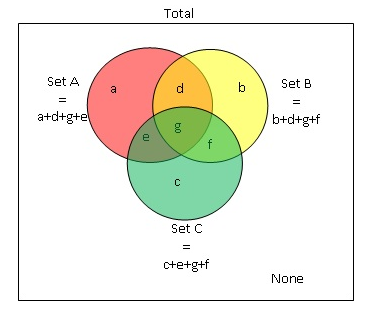 FIRST FORMULA
FIRST FORMULA\(Total = A + B + C - (sum \ of \ 2-group \ overlaps) + (all \ three) + Neither\).
Let's see how this formula is derived.
When we add three groups A, B, and C some sections are counted more than once. For instance: sections
d,
e, and
f are counted twice and section
g thrice.
Hence we need to subtract sections d, e, and f ONCE (to count section g only once) and subtract section g TWICE (again to count section g only once).In the formula above, \(sum \ of \ 2-group \ overlaps=AnB+AnC+BnC\), where AnB means intersection of A and B (sections
d, and
g), AnC means intersection of A and C (sections
e, and
g), and BnC means intersection of B and C (sections
f, and
g).
Now, when we subtract \(AnB\) (
d, and
g), \(AnC\) (
e, and
g), and \(BnC\) (
f, and
g) from \(A+B+C\), we are subtract sections
d,
e, and
f ONCE
BUT section
g THREE TIMES (and we need to subtract section
g only twice), therefor we should add only section
g, which is intersection of A, B and C (AnBnC) again to get \(Total = A + B + C - (sum \ of \ 2-group \ overlaps) + (all \ three) + Neither\).
SECOND FORMULA\(Total = A + B + C - (sum \ of \ EXACTLY \ 2-group \ overlaps) - 2*(all \ three) + Neither\).
Notice that
EXACTLY (only) 2-group overlaps is not the same as
2-group overlaps:
Elements which are common only for A and B are in section
d (so elements which are common ONLY for A and B refer to the elements which are in A and B but not in C);
Elements which are common only for A and C are in section
e;
Elements which are common only for B and C are in section
f.
Let's see how this formula is derived.
Again: when we add three groups A, B, and C some sections are counted more than once. For instance: sections
d,
e, and
f are counted twice and section
g thrice. Hence
we need to subtract sections d, e, and f ONCE (to count section
g only once) and
subtract section g TWICE (again to count section
g only once).
When we subtract \(sum \ of \ EXACTLY \ 2-group \ overlaps\) from A+B+C we subtract sections
d,
e, and
f once (fine) and next we need to subtract ONLY section
g (\(AnBnC\)) twice. That's it.
Can we say that Set A= a+d+e+g
B=b+d+f+g
C=e+g+f+c
Now if you add A+B+C= a+b+c +3g+2e+2f+2d but ideally all the elements should be there once. So we need to subtract e,f and d once and g twice
Now if you have case 1: where you have the following values
\(Total = A + B + C - (sum \ of \ 2-group \ overlaps) + (all \ three) + Neither\).
Sum of 2 group overlaps:Which values represent 2 group overlap, namely d+g,e+g and f+g, so here you have taken d,e and f only once to Subtract from SET A,B, and C values,where as g has been counted thrice and thus will be subtracted thrice from Set A,B and C values...
Note we need 1 value of all elements to count the Total
Total= Set A+SetB+SetC -{d+g+e+g+f+g} +g(all 3 overlaps) +neither
Why??
If you put elements of Set A,B and C you get :a+b+c +3g+2e+2f+2d - {d+g+e+g+f+g} +g(add g) +neither
Total= a+b+c+d+e+f+g+NeitherCase 2 : where
\(Total = A + B + C - (sum \ of \ EXACTLY \ 2-group \ overlaps) - 2*(all \ three) + Neither\).
a+b+c +3g+2e+2f+2d-{d+e+f} -2g +neither
TOTAL= a+b+c+d+e+f+g+neitherSo you need to know which values are given then use the relevant forumla.
