If -6 < X < 7 and -8 < Y < 5, which of the following specifies all the

To determine the largest possible value of XY, we either multiply together the two smallest negative values or the two largest positive values. Since (-6)(-8) = 48 and (7)(5) = 35 and 48 > 35, we see that the largest possible product of X and Y is less than 48.

To determine the smallest value of XY, we multiply the largest positive number by the smallest negative number. Thus, the product of X and Y must be greater than (-8)(7) = -56. Thus:

-56 < XY < 48

Answer: D

By using all the four numbers let us make the smallest value = -8*7 = -56

Largest value = 8*6 = 48

Therefore, D.

I dont understand. The question did not say that X is less than OR EQUAL TO -6 or more than or equal to 7 , so we shouldn't count -6 and 7 as a possibility of x right? Same goes for Y

Sandy56 , I think you got confused about what a strict inequality means.
Actually, maybe just confused about inequality, full stop.
Inequalities are occasionally disorienting. Too, I might be missing something.

The prompt defines the possible values of X and Y in terms of strict inequalities.

Less than and NEVER equal to: <
Greater than and NEVER equal to: >

Another way to understand "strict inequality"
The strict inequality signs < and > mean that the variable can never equal the number next to it

Strict inequalities do not look like this: ≤ ≥

Of course the prompt did NOT say that X is less than or equal to -6
Why would the prompt say the opposite of what the inequality indicates? (Wow am I perplexed. )

The strict inequality that defines the values of X is -6 < X < 7
X is greater than and never/not equal to -6, and X is less than and not equal to 7
Possible values of X can fall only in the range between -6 and 7

Given the inequality's range of possible values for X, how could X be equal to -6, less than -6, equal to 7, or greater than 7?

The prompt says none of the possibilities you suggest because if it were to say any of those things, it would render the inequalities meaningless.
(Okay, now I am overboard. Prompts do not talk. Run with it.)

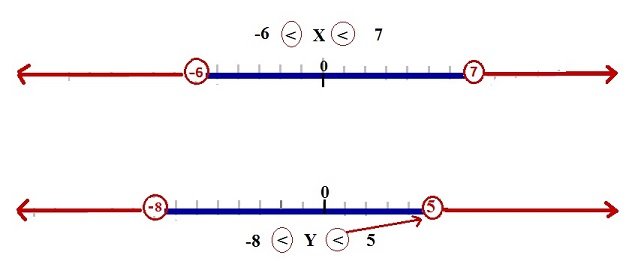
Number lines (diagram) offer a graphic representation of the inequalities that define permissible and impermissible ranges for values of X and Y
Possible values for X or Y: BLUE
X and Y cannot fall in the ranges that are RED; nor can the variables equal the circled numbers
Circled numbers give us the values that X and Y must be between
X and Y cannot hop over, disregard, or obliterate their boundaries.

If a strict inequality gives a range of possible values for X, that range IS all the possible values.

I hope that helps.

Thank you for your reply,
I think you confused my question since it wasnt clear. What I meant to say is that I did not understand why x = -8 and y = -6 since the question did not have a >= sign on it.
I thought that the largest number for x should be -7 and y= -5 so making the answer 35

Posted from my mobile device

Hi Sandy56,

I try to help you. The way I am looking your concern is why x = - 8 , y = -6 and not x = -7, y = - 5. And you are thinking of this because question nowhere says that - 8 and -6 are inclusive in the range with <= or > = sign.

See the highlighted part above written by you. It says "largest number" and not "largest integer" .

What if the values are - 7.5 * -5.5 = 41.25 > 35

Question says all possible values and not all possible integer values.

It can be - 7.99 * - 5.99 = 47.87, which will be greater the - 7 * - 5 but always smaller than - 8 * - 6.

So we can't take -7* -5.

To cover all the values we have to take -8*-6 = 48

Hope I have answered your question.