Events & Promotions
|
|
GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
May 1912:00 PM PDT
-01:00 PM PDT
Scoring 329 on the GRE is not always about using more books, more courses, or a longer study plan. In this episode of GRE Success Talks, Ashutosh shares his GRE preparation strategy, study plan, and test-day experience, explaining how he kept his prep....
May 1212:00 PM EDT
-11:59 PM EDT
Make the most of your break with the most realistic GMAT™ prep. Take up to $700 off select products. Ends 6/1
May 1501:00 PM IST
-11:00 AM IST
Start your journey with a fully customized action plan and work with a dedicated mentor to achieve a 735+ score.- May 18
10:00 AM PDT
-11:00 AM PDT
Join us in a live GMAT practice session and solve 25 challenging GMAT questions with other test takers in timed conditions, covering GMAT Quant, Data Sufficiency, Data Insights, Reading Comprehension, and Critical Reasoning questions. - Jun 10
06:00 AM PDT
-06:15 PM PDT
Register for the GMAT Club Virtual MBA Spotlight Fair – the world’s premier event for serious MBA candidates. This is your chance to hear directly from Admissions Directors at nearly every Top 30 MBA program..
26 Sep 2017, 00:23
Kudos
Bookmarks
C
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
95%
(hard)
Question Stats:
42% (02:35) correct
58%
(02:21)
wrong
based on 91
sessions
History
Date
Time
Result
Not Attempted Yet
In the rectangle above, if the unshaded region is equilateral and equiangular, what fractional part of the rectangular region is shaded?
(A) 1/6
(B) 2/9
(C) 1/4
(D) 1/3
(E) 4/9
Attachment:
2017-09-26_1117.png [ 4.23 KiB | Viewed 9228 times ]
26 Sep 2017, 04:51
Kudos
Bookmarks
Attachment:
2017-09-26_1117.png [ 5.34 KiB | Viewed 8373 times ]
Since the unshaded region is equilateral and equiangular,
the hexagon within the rectangle will have 6 equilateral triangles.
Each equilateral triangle will further contain two triangles of equal area.
These smaller triangles have an area equal to the shaded triangles,
because they have same base and height as the shaded triangles.
The hexagon itself will have 12 triangles(each of which has the same area as the shaded triangle)
There are a total of 16(12+4) smaller triangles of equal area within the rectangle and
the fractional part of the rectangular region which is shaded is \(\frac{4}{16} = \frac{1}{4}\)(Option C)
26 Sep 2017, 08:36
Kudos
Bookmarks
Bunuel
Attachment:
hexsquare.png [ 21.19 KiB | Viewed 8234 times ]
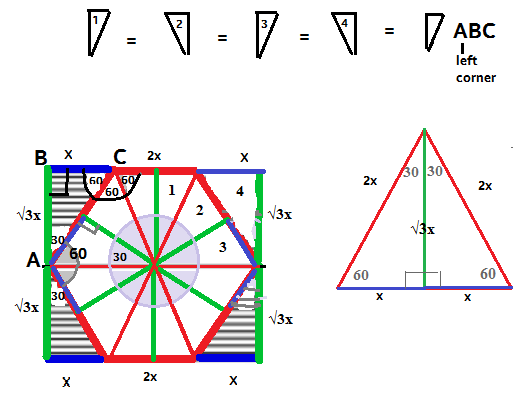
1. SIX EQUILATERAL TRIANGLES IN THE HEXAGON
This regular hexagon (equal angles, equal sides) can be divided into 6 equilateral triangles
Diagram: each equilateral triangle has side 2x
2. EACH EQUILATERAL TRIANGLE DIVIDES INTO TWO CONGRUENT RIGHT TRIANGLES - see diagram, triangle on right
Equilateral triangles can be divided into 2 congruent right triangles 30-60-90 right triangles because:
--An equilateral triangle's median is also its angle bisector and perpendicular bisector
--One 60-degree vertex is bisected into a 30-degree angle in each right triangle
--The perpendicular bisector creates two 90-degree angles in each right triangle
-- Finally, the last vertex of the right triangle on both sides has measure of 60 degrees
SIDE RATIO OF 30-60-90 TRIANGLES
--30-60-90 triangles have sides in ratio \(x: x\sqrt{3}: 2x\)
3. HEXAGON HAS 12 CONGRUENT RIGHT TRIANGLES
There are 12 such identical triangles in the hexagon. SIX equilateral triangles * TWO right triangles each = 12 identical right triangles inside the hexagon
4. SHADED AREAS ARE IDENTICAL TO THE 12 RIGHT TRIANGLES INSIDE THE HEXAGON
The shaded areas (the corners of the rectangle) are congruent with all the right triangles inside the hexagon
Angles are congruent
--Each corner triangle is a 30-60-90 triangle - on diagram, see triangle ABC and the left side of the rectangle
-- 30- degree angle is on the straight line - see left side of rectangle
On that line, whose angles sum to 180, lies a 120-degree angle of a hexagon (or two 60-degree angles of the divided triangles)
180 - 60 - 60 = 60 degrees are left to be divided into two equal angles. On the line, each corner has a 30-degree angle
-- Each corner triangle has a 90-degree angle (by definition of rectangle)
-- Each corner triangle has a 60-degree angle - see left corner triangle, vertex C
Side lengths are equal
--Each corner triangle has exactly the same lengths as the 12 small triangles inside the hexagon: \(x, x\sqrt{3},\) and \(2x\) (see diagram)
5. FRACTION OF RECTANGLE SHADED?
12 triangles inside hexagon, 4 outside = 16 in rectangle. Four are shaded.
\(\frac{4}{16} = \frac{1}{4}\)
ANSWER C
