[GMAT math practice question]
(geometry) In the figure, ABC is a right triangle. What is the area of ABC?
Attachment:
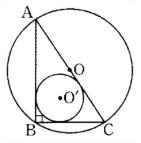 8.19 DS.png [ 11.32 KiB | Viewed 1435 times ]
8.19 DS.png [ 11.32 KiB | Viewed 1435 times ]
1) Circle O circumscribes triangle ABC and has diameter 13
2) Circle O’ is inscribed in triangle ABC and has diameter 6
=>
Forget conventional ways of solving math questions. For DS problems, the VA (Variable Approach) method is the quickest and easiest way to find the answer without actually solving the problem. Remember that equal numbers of variables and independent equations ensure a solution.
2 variables are required to specify the two circles, and two variables are required to specify the right triangle. So, we have 4 variables. Since one side of the triangle is equal to the diameter of one of the two circles, we have 1 equation.
Since we have 4 variables and 1 equation, E is most likely to be the answer. So, we should consider conditions 1) & 2) together first. After comparing the number of variables and the number of equations, we can save time by considering conditions 1) & 2) together first.
Attachment:
 8.21ads.png [ 7.09 KiB | Viewed 1440 times ]
8.21ads.png [ 7.09 KiB | Viewed 1440 times ]
Conditions 1) & 2)
Since the radius of O’ is 3, BE = BD = O’E = 3.
Suppose the length of AD is a.
Then AF = AD = a, and CF = CE = 13-a.
So, BC = BE + EC = 3 + 13 – a = 16 – a,
And AB = AD + DB = a + 3.
Thus, the area of triangle ABC is (1/2)(AB+BC+CA)(3) = (1/2)(a+3+16-a+13)(3) = 48
Therefore, C is the answer.
Answer: C
In cases where 3 or more additional equations are required, such as for original conditions with “3 variables”, or “4 variables and 1 equation”, or “5 variables and 2 equations”, conditions 1) and 2) usually supply only one additional equation. Therefore, there is an 80% chance that E is the answer, a 15% chance that C is the answer, and a 5% chance that the answer is A, B or D. Since E (i.e. conditions 1) & 2) are NOT sufficient, when taken together) is most likely to be the answer, it is generally most efficient to begin by checking the sufficiency of conditions 1) and 2), when taken together. Obviously, there may be occasions on which the answer is A, B, C or D.

