Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Kudos
Bookmarks
In the first part of this article, yesterday, we highlighted the importance of smart calculations as a way to hit the ground running, while preparing for GMAT Quant.
In case you have not had a look at it yet, click on this link: Smart calculations - Part 1
In the second part of this article, we will discuss a few methods which will help you develop a mindset of observing the numbers before adding them. We shall also discuss a couple of effective methods to subtract any two numbers very quickly. As mentioned in the first part of this article, the objective of these methods is not only to add a potent weapon to your arsenal to handle the calculations that come up on GMAT Quant questions but also to help you develop a habit of speeding up your calculations so that you can have more time to analyse the question.
So, let's get started!
Methods for Quick Addition:
Addition is probably the simplest of all the 4 basic mathematical operations. Yet, many of us make mistakes while adding values, especially when hard pressed for time. 47 + 18 can suddenly become 75; 87 + 87 can magically become 164
The reason for this, partially, is a bit of complacency because we feel “Hey, come on, I can’t go wrong in adding these values”. However, the bigger reason is the time pressure – the clock ticking at the back of our head (not the one ticking on the screen). A small part of it is just a design flaw by the almighty – somehow, we all have that one mistake we make when we calculate.
Whatever be the reasons, I’m sure all of us would like to cut down the mistakes we make in addition – come on, that’s something under our control.
So, let’s take a look at two methods that can help make addition faster and precise.
1) Method of place values
2) Method of unit digit
Method of place values
This is an easy method to learn and get better at. In this method, every number can be broken up into the respective thousands, hundreds, tens, units etc.,
A great way to remember this is to think of money. For example, if $642 is to be dispensed, one way is to have 6 hundreds, 4 tens and 2 ones. Now, if you need to add an amount of $735 to this, we first break down the number into 7 hundreds, 3 tens and 5 ones. All that is left is to add the respective hundreds, tens and ones values – this gives us 13 hundreds, 7 tens and 7 ones; therefore, 1377.
Let’s pick a sample set of numbers to add – say, 484, 529, 676 and 841.
484 = 400 + 80 + 4
529 = 500 + 20 + 9
676 = 600 + 70 + 6
841 = 800 + 40 + 1
Adding the hundreds, we have 2300; adding the tens, we have 210, adding the ones, we have 20 giving us a sum of 2530.
Now, that you have understood how simple and logical this technique is, try adding 1032, 1089, 1156, 1225 and 1296.
Did you get 5798? Well done, you seem to have picked up the nuances of this method of quick addition.
(How many of you noticed that all the numbers which were added in the last calculation are perfect squares? )
)
Method of Units digit
This method requires you to have good observation skills. Like the previous method, this is also based on simple but sound logic.
In this method, the objective is to obtain a number that ends with ZERO – by pairing numbers whose digits are 9 and 1 / 8 and 2 / 4 and 6 and so on – so that we can then add these numbers ending with ZERO since doing that is much easier.
For example, if we have to add the numbers 61, 68, 73, 79, 82, 87 and 90,
we pair the 61 with 79 to obtain 140
we pair the 68 with 82 to obtain 150
we pair the 73 with 87 to obtain 160
Now, it’s easy to add these numbers together and then add it with 90. The sum of these numbers = 140 + 160 + 150 + 90 = 540.
Notice how we added 140 and 160 first, rather than adding them randomly; this is because we know that 14 and 16 give is 30 when added.
This method not only help you add faster, but, more importantly, it helps you build a smart mindset of observing numbers and understanding smaller details about them before performing any operation on them. And that’s why this method is doubly important to learn and perfect.
Let’s pick another sample set of numbers to add – 226, 101, 674, 399, and 770.
Pairing the 226 with 674, we obtain 900
Pairing the 101 with 399, we obtain 500
Adding the above to obtain 1400 and then adding 770 gives us a sum of 2170.
Try your hand at adding these numbers using the Units digit approach: 216, 512, 729, 1000, 331, 728 and 744
So, those were two simple but effective methods to add faster. A good idea to get better at these methods is to pick random 2-digit and 3-digit numbers (4-digit numbers also, if you want to, but the chances of that happening on the GMAT are remote) and apply both of these approaches to get to the answer. Slowly, but steadily, you will realise that a certain method works better for you and you can then stick to that method of adding numbers.
With this, it’s time to look at a few methods of quick subtractions.
Methods for Quick Subtraction
Subtraction, on the other hand, is not as intuitive to us as addition. Is it because of having to take the carry over? Probably. But one thing is for sure – given a choice between adding fast and subtracting fast, most of us would pick the former. One more fundamental difference between addition and subtraction is that, we subtract only two numbers at a time, unlike addition where we can add more than 2 numbers simultaneously, hence it's more time consuming.
Therefore, one of the methods to subtract faster employs addition as its primary operation. It also employs the Number line in order to do so.
The other method uses the distance of hundred, which is known as the Hundred’s complement, to help you subtract numbers where, carrying over is inevitable. Of course, this method requires extensive practice before which it can start giving you results.
Number line method
In the number line method, we flip the operation of subtraction on its head and actually use addition to find the distance between two numbers.
Let’s take an example to understand this method – say 787 is to be subtracted from 932.
Let’s plug 787 on the number line. The difference between 800 and 787 is 13; the difference between 932 and 800 is 132; therefore, the difference between 932 and 787 is 145, which is the addition of 13 and 132.
By converting a tricky process like subtraction to addition, we make the process more reliable.
Method of Hundreds complement
This method is extremely useful when the subtraction involves carrying over from the left to the right.
For example, if 387 has to be subtracted from 561, we observe that 87 is bigger than 61 and therefore, we have to take a carry, which has scope for mistakes.
The hundreds complement method has the following steps:
1) Divide the given number into two parts – the part on the right to contain the last 2 digits of the given numbers and the part on the left containing the remaining digits of the given numbers.
For example, if 387 has to be subtracted from 561, then we write it as
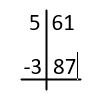
Subtract - 1.JPG [ 9.26 KiB | Viewed 3146 times ]
2) Consider the last two digits of the number(part on the right) to be subtracted (the number below) and find its hundreds complement.
The hundreds complement of any number is its distance from 100.
In our example, we find the hundreds complement of 87, which is 13.
3) Add this hundreds complement to the last two digits of the number(part on the right) above, to obtain the last two digits of the result.
In our example, we add 13 to 61 to obtain 74 as the last two digits of our final result.
4) Subtract 1 from the number formed by the remaining digits of the number (part on the left) at the top (i.e. the number from which we are subtracting)
In our example, 5 is the remaining part of the number, so we subtract 1 from 5 to get 4, which is the result of this step.
5) From the result of the previous step, subtract the number formed by the remaining digits of the number (part on the left) at the bottom (i.e. the number which is being subtracted). The resultant number will form the remaining digits of the final result.
In our example, we subtract 3 from 4 to obtain 1.
Therefore, 561 – 387 = 174.
As you see, this method has many small steps and therefore requires lot more practice to become confident. However, once you perfect the art, this is a great tool to subtract big numbers quickly.
Let’s take another example. Say, we have to subtract 4598 from 6872.
So, 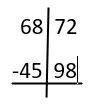
Subtract - 2.JPG [ 9.69 KiB | Viewed 3128 times ]
Hundreds complement of 98 is 2. Adding 2 to 72, we get 74. 74 represents the last 2 digits of the result.
Subtracting 1 from 68, we get 67. Subtracting 45 from 67, we have 22. 22 represents the remaining digits of the result.
Therefore, 6872 – 4598 = 2274
We hope that the second example has clarified any doubts that you may have had when you were reading through the different steps involved in this technique.
If you are clear, go ahead, take a few examples of your own and try out this technique on them. If you are unclear, it's best to go through the examples once again, slowly and steadily, and we are sure you will understand the method then.
So, that’s it for the second part of this article, in which we covered a couple of methods each for quick addition and subtraction.
We hope that you had fun learning these new methods. As we mentioned, you will have to consistently practice these methods over the next few days before you start seeing consistent results from these. Therefore, here are a few questions for you to practice.
Of course, feel free to take your own values and practice more, because the more you use these methods, the better you get at them.
We would like to caution you against comparing the efficacy of these methods with the methods you have been using till now – remember, you are just taking baby steps in these methods, so comparing them to your old methods wouldn’t be an apples-to-apples comparison.
In the third part of this article tomorrow, we shall be discussing some methods for quick multiplication. Please watch out for the same.
Goodbye!
In case you have not had a look at it yet, click on this link: Smart calculations - Part 1
In the second part of this article, we will discuss a few methods which will help you develop a mindset of observing the numbers before adding them. We shall also discuss a couple of effective methods to subtract any two numbers very quickly. As mentioned in the first part of this article, the objective of these methods is not only to add a potent weapon to your arsenal to handle the calculations that come up on GMAT Quant questions but also to help you develop a habit of speeding up your calculations so that you can have more time to analyse the question.
So, let's get started!
Methods for Quick Addition:
Addition is probably the simplest of all the 4 basic mathematical operations. Yet, many of us make mistakes while adding values, especially when hard pressed for time. 47 + 18 can suddenly become 75; 87 + 87 can magically become 164
The reason for this, partially, is a bit of complacency because we feel “Hey, come on, I can’t go wrong in adding these values”. However, the bigger reason is the time pressure – the clock ticking at the back of our head (not the one ticking on the screen). A small part of it is just a design flaw by the almighty – somehow, we all have that one mistake we make when we calculate.
Whatever be the reasons, I’m sure all of us would like to cut down the mistakes we make in addition – come on, that’s something under our control.
So, let’s take a look at two methods that can help make addition faster and precise.
1) Method of place values
2) Method of unit digit
Method of place values
This is an easy method to learn and get better at. In this method, every number can be broken up into the respective thousands, hundreds, tens, units etc.,
A great way to remember this is to think of money. For example, if $642 is to be dispensed, one way is to have 6 hundreds, 4 tens and 2 ones. Now, if you need to add an amount of $735 to this, we first break down the number into 7 hundreds, 3 tens and 5 ones. All that is left is to add the respective hundreds, tens and ones values – this gives us 13 hundreds, 7 tens and 7 ones; therefore, 1377.
Let’s pick a sample set of numbers to add – say, 484, 529, 676 and 841.
484 = 400 + 80 + 4
529 = 500 + 20 + 9
676 = 600 + 70 + 6
841 = 800 + 40 + 1
Adding the hundreds, we have 2300; adding the tens, we have 210, adding the ones, we have 20 giving us a sum of 2530.
Now, that you have understood how simple and logical this technique is, try adding 1032, 1089, 1156, 1225 and 1296.
Did you get 5798? Well done, you seem to have picked up the nuances of this method of quick addition.
(How many of you noticed that all the numbers which were added in the last calculation are perfect squares?
Method of Units digit
This method requires you to have good observation skills. Like the previous method, this is also based on simple but sound logic.
In this method, the objective is to obtain a number that ends with ZERO – by pairing numbers whose digits are 9 and 1 / 8 and 2 / 4 and 6 and so on – so that we can then add these numbers ending with ZERO since doing that is much easier.
For example, if we have to add the numbers 61, 68, 73, 79, 82, 87 and 90,
we pair the 61 with 79 to obtain 140
we pair the 68 with 82 to obtain 150
we pair the 73 with 87 to obtain 160
Now, it’s easy to add these numbers together and then add it with 90. The sum of these numbers = 140 + 160 + 150 + 90 = 540.
Notice how we added 140 and 160 first, rather than adding them randomly; this is because we know that 14 and 16 give is 30 when added.
This method not only help you add faster, but, more importantly, it helps you build a smart mindset of observing numbers and understanding smaller details about them before performing any operation on them. And that’s why this method is doubly important to learn and perfect.
Let’s pick another sample set of numbers to add – 226, 101, 674, 399, and 770.
Pairing the 226 with 674, we obtain 900
Pairing the 101 with 399, we obtain 500
Adding the above to obtain 1400 and then adding 770 gives us a sum of 2170.
Try your hand at adding these numbers using the Units digit approach: 216, 512, 729, 1000, 331, 728 and 744
So, those were two simple but effective methods to add faster. A good idea to get better at these methods is to pick random 2-digit and 3-digit numbers (4-digit numbers also, if you want to, but the chances of that happening on the GMAT are remote) and apply both of these approaches to get to the answer. Slowly, but steadily, you will realise that a certain method works better for you and you can then stick to that method of adding numbers.
With this, it’s time to look at a few methods of quick subtractions.
Methods for Quick Subtraction
Subtraction, on the other hand, is not as intuitive to us as addition. Is it because of having to take the carry over? Probably. But one thing is for sure – given a choice between adding fast and subtracting fast, most of us would pick the former. One more fundamental difference between addition and subtraction is that, we subtract only two numbers at a time, unlike addition where we can add more than 2 numbers simultaneously, hence it's more time consuming.
Therefore, one of the methods to subtract faster employs addition as its primary operation. It also employs the Number line in order to do so.
The other method uses the distance of hundred, which is known as the Hundred’s complement, to help you subtract numbers where, carrying over is inevitable. Of course, this method requires extensive practice before which it can start giving you results.
Number line method
In the number line method, we flip the operation of subtraction on its head and actually use addition to find the distance between two numbers.
Let’s take an example to understand this method – say 787 is to be subtracted from 932.
Let’s plug 787 on the number line. The difference between 800 and 787 is 13; the difference between 932 and 800 is 132; therefore, the difference between 932 and 787 is 145, which is the addition of 13 and 132.
By converting a tricky process like subtraction to addition, we make the process more reliable.
Method of Hundreds complement
This method is extremely useful when the subtraction involves carrying over from the left to the right.
For example, if 387 has to be subtracted from 561, we observe that 87 is bigger than 61 and therefore, we have to take a carry, which has scope for mistakes.
The hundreds complement method has the following steps:
1) Divide the given number into two parts – the part on the right to contain the last 2 digits of the given numbers and the part on the left containing the remaining digits of the given numbers.
For example, if 387 has to be subtracted from 561, then we write it as
Attachment:
Subtract - 1.JPG [ 9.26 KiB | Viewed 3146 times ]
2) Consider the last two digits of the number(part on the right) to be subtracted (the number below) and find its hundreds complement.
The hundreds complement of any number is its distance from 100.
In our example, we find the hundreds complement of 87, which is 13.
3) Add this hundreds complement to the last two digits of the number(part on the right) above, to obtain the last two digits of the result.
In our example, we add 13 to 61 to obtain 74 as the last two digits of our final result.
4) Subtract 1 from the number formed by the remaining digits of the number (part on the left) at the top (i.e. the number from which we are subtracting)
In our example, 5 is the remaining part of the number, so we subtract 1 from 5 to get 4, which is the result of this step.
5) From the result of the previous step, subtract the number formed by the remaining digits of the number (part on the left) at the bottom (i.e. the number which is being subtracted). The resultant number will form the remaining digits of the final result.
In our example, we subtract 3 from 4 to obtain 1.
Therefore, 561 – 387 = 174.
As you see, this method has many small steps and therefore requires lot more practice to become confident. However, once you perfect the art, this is a great tool to subtract big numbers quickly.
Let’s take another example. Say, we have to subtract 4598 from 6872.
So,
Attachment:
Subtract - 2.JPG [ 9.69 KiB | Viewed 3128 times ]
Hundreds complement of 98 is 2. Adding 2 to 72, we get 74. 74 represents the last 2 digits of the result.
Subtracting 1 from 68, we get 67. Subtracting 45 from 67, we have 22. 22 represents the remaining digits of the result.
Therefore, 6872 – 4598 = 2274
We hope that the second example has clarified any doubts that you may have had when you were reading through the different steps involved in this technique.
If you are clear, go ahead, take a few examples of your own and try out this technique on them. If you are unclear, it's best to go through the examples once again, slowly and steadily, and we are sure you will understand the method then.
So, that’s it for the second part of this article, in which we covered a couple of methods each for quick addition and subtraction.
We hope that you had fun learning these new methods. As we mentioned, you will have to consistently practice these methods over the next few days before you start seeing consistent results from these. Therefore, here are a few questions for you to practice.
- Find the sum of 117, 361, 478, 522, 639, 883 and 900.
Find the sum of 1248, 1402, 1592, 2627 and 3078.
Subtract 3979 from 7945
Subtract 9897 from 42363
Subtract 90866 from 113444
Of course, feel free to take your own values and practice more, because the more you use these methods, the better you get at them.
We would like to caution you against comparing the efficacy of these methods with the methods you have been using till now – remember, you are just taking baby steps in these methods, so comparing them to your old methods wouldn’t be an apples-to-apples comparison.
In the third part of this article tomorrow, we shall be discussing some methods for quick multiplication. Please watch out for the same.
Goodbye!
Kudos
Bookmarks
In the first and second parts of this article, we highlighted the importance of smart calculations and how they can help you become a better observer of numbers, as you prepare to ace the Quant section of the GMAT. We also discussed some smart methods for quick addition and subtraction.
In case you have not had a look at these yet, click on these links:
Smart calculations - Part 1
Smart calculations - Part 2
In the third part of this article, we will discuss a few methods which will help you multiply faster; we will also discuss how to leverage the Distributive law to speed up calculations. By the end of today’s part, you would have picked up some very valuable techniques that can fast track your calculations on GMAT quant questions, considering that many questions in the Quant section require you to perform multiplication.
So, let’s get started!
Multiplication is a process of repeated addition. Multiplying 3 with 4 is equivalent to adding 3 four times / adding 4 three times. However, difficulties increase as the numbers become bigger.
Conventional multiplication involves multiplying each digit of one number with each digit of the other number in a step-by-step process and then adding up the columns to get the final product. This is time-consuming and prone to a lot of errors.
Therefore, let’s look at a few methods to multiply quickly without compromising on accuracy.
Using the distributive law
As with many aspects in life, sometimes, the simple things are easily forgotten but it’s the simple things that actually make life easier. Something similar can be thought of when it comes to making calculations fun and fast – the good old Distributive law.
Two versions of the distributive law can actually make your multiplication process faster. In fact, the GMAT expects you to apply such techniques from high-school Math than to just perform multiplication by brute-force.
As per the distributive law, a(b+c) = ab + ac; also, a(b-c) = ab – ac.
These two versions are immensely useful for speeding up calculations, especially if you have built up the mindset to observe numbers, as we had mentioned in the first two parts.
Let’s take a few examples to understand better.
Example 1: Multiply 45 * 30.
45 * 30 = (40 + 5) * 30 = 40 * 30 + 5 * 30 = 1200 + 150 = 1350
Example 2: Multiply 15 with 13.8
15 (13.8) = 15 (14 – 0.2) = 15 (10 + 4 – 0.2) = 15 * 10 + 15 * 4 – 15 * 0.2 = 150 + 60 – 3 = 207.
Example 3: Multiply 42 with 17
42 (17) = 42(10 + 5 + 2) = 420 + 210 + 84 = 714 (note how it’s easy to find 42 * 5 if you know 42 * 10. GMAT expects you to do such smart calculations)
It can also be done by distributing the 42 while keeping the 17 constant.
17(42) = 17(40 + 2) = 680 + 34 = 714.
Therefore, flexibility is the biggest advantage of using the Distributive law. Based on your knowledge of multiplication tables, you can choose to break up the numbers that can help you multiply easily and quickly, rather than having to be one-dimensional.
And that’s the reason why we have put this method ahead of a couple of other speed math methods, in this article. If you know how to leverage the distributive law, you can make better use of the other two methods that we are going to describe now. These are:
Each of these methods have their own advantages as well as limitations. While the single line method is broader in its application, the base method is more specific in where it can be applied. As such, the single line method requires consistent practice for a higher duration of time.
So, let’s look at both of these methods, one by one.
Single line method:
The single line method is so called because the final product is obtained in a single line, however big/small the multiplicands (the numbers being multiplied are known as multiplicands) are, unlike the conventional methods where we have rows and rows of numbers as the digits in the multiplicands increase.
Let's take an example where we try to multiply, say 43 with 37.
Step 1: Multiply the respective unit digits, 3 and 7 to get 21. We put the 1 as the unit digit of the result and take 2 as the carryover

SLM Step 1 Ex 1.JPG [ 11.34 KiB | Viewed 2808 times ]
Step 2: Cross multiply the units digit and the tens digit of each number and add the result. Do not forget to add the 2 that was carried over from the previous step. The unit digit of the result is taken and the rest is carried over.
Therefore, the result of this step = 7*4 + 3* 3 + 2 = 39

SLM Step 2 Ex 1.JPG [ 12.88 KiB | Viewed 2817 times ]
Step 3: Lastly, multiply the respective tens digits and add the number carried over from the previous step. The result will represent the remaining digits of the product.
In this case, multiply 4 with 3 to obtain 12 and add the carryover of 3 to get 15.
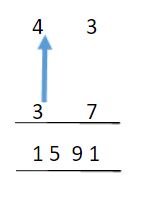
SLM Step 3 Ex 1.JPG [ 10.17 KiB | Viewed 2801 times ]
Now, you can go ahead and cross-verify if your answer is right 😊.
Let’s take another example to consolidate our learnings. Let’s try to multiply 57 with 29.
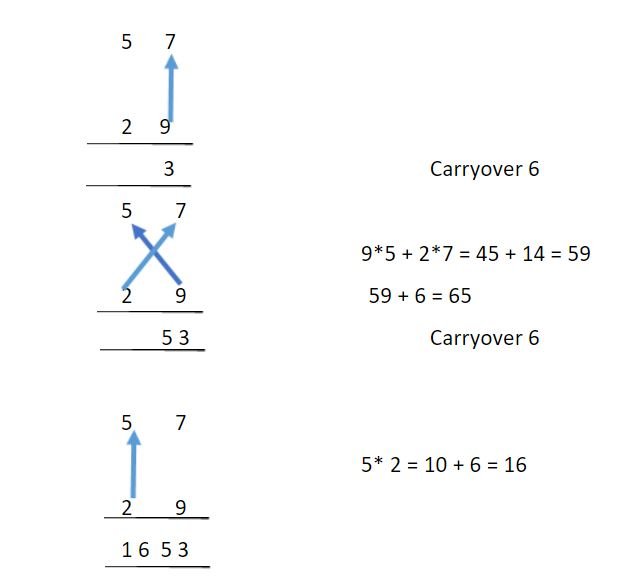
SLM Ex 2.JPG [ 26.94 KiB | Viewed 2786 times ]
Now that you have understood this method well, go ahead and take a few random two-digit numbers and practice this method till you get comfortable with it.
Base Method
As mentioned earlier, the base method can only be applied with specific numbers. However, it is a very powerful method in cases where it can be applied. It’s very simple to understand, practice and actually apply when needed.
The base method is applied when two numbers are very close to a reference number, which can typically be numbers like 10, 50, 100 and so on.
Let’s take an example to understand how it works. Let's try to multiply 15 with 16 (these are easy numbers to multiply even with the conventional method so that you may cross verify your answer)
Since 15 and 16 are both close to the number 10, the base for this calculation is 10.
Step 1: 15 – 10 = 5 and 16 – 10 = 6. . We arrange the numbers as shown below:

BM Step 1 Ex 1.JPG [ 8.95 KiB | Viewed 2826 times ]
The 5 and 6 here are the respective distances of 15 and 16 from the base, 10.
Step 2: We add the numbers in the direction of the arrows to get 21 in both cases. This is followed by multiplying this resultant number with the base
Since the base is 10, we multiply 21 with 10 to obtain 210 which is the result of this step
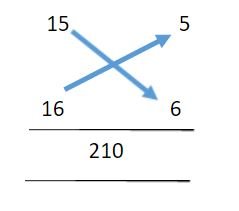
BM Step 2 Ex 1.JPG [ 11.81 KiB | Viewed 2791 times ]
Step 3: We multiply the numbers in the direction of the arrow and add it to the result of the previous step. The final sum represents the product of the given numbers.

BM Step 3 Ex 1.JPG [ 12.93 KiB | Viewed 2793 times ]
Let’s take another example, which represents a variation. If we have to multiply 23 * 18. We see that both numbers are close to the number 20; therefore, the base for this calculation is 20.
Let’s arrange the numbers as we did in the previous case:
BM Step 1 Ex 2.JPG [ 8.98 KiB | Viewed 2789 times ]
The 3 and -2 here are the respective distances of 23 and 18 from the base, 20. (Note that the distance of 18 from 20 is -2 since 18 is smaller. This is a convention followed in this method)
We add the numbers in the direction of the arrows to get 21 in both cases. Note that adding -2 to 23 gives 21. Since the base is 20, we multiply 21 with 20 to obtain 420 which is the result of this step
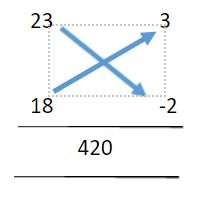
BM Step 2 Ex 2.JPG [ 12.59 KiB | Viewed 2796 times ]
We multiply the numbers in the direction of the arrow and add it to the result of the previous step
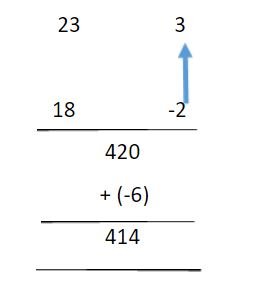
BM Step 3 Ex 2.JPG [ 12.65 KiB | Viewed 2759 times ]
We hope that this method is clear to you now. As always, go ahead and take some examples of your own and try to get comfortable with this method to the extent that you will start using it in your calculations.
With this, we conclude the third part of this article on smart calculations. In the fourth part of this article, tomorrow, we will be discussing methods to calculate squares and cubes of two-digit numbers.
Goodbye!
In case you have not had a look at these yet, click on these links:
Smart calculations - Part 1
Smart calculations - Part 2
In the third part of this article, we will discuss a few methods which will help you multiply faster; we will also discuss how to leverage the Distributive law to speed up calculations. By the end of today’s part, you would have picked up some very valuable techniques that can fast track your calculations on GMAT quant questions, considering that many questions in the Quant section require you to perform multiplication.
So, let’s get started!
Multiplication is a process of repeated addition. Multiplying 3 with 4 is equivalent to adding 3 four times / adding 4 three times. However, difficulties increase as the numbers become bigger.
Conventional multiplication involves multiplying each digit of one number with each digit of the other number in a step-by-step process and then adding up the columns to get the final product. This is time-consuming and prone to a lot of errors.
Therefore, let’s look at a few methods to multiply quickly without compromising on accuracy.
Using the distributive law
As with many aspects in life, sometimes, the simple things are easily forgotten but it’s the simple things that actually make life easier. Something similar can be thought of when it comes to making calculations fun and fast – the good old Distributive law.
Two versions of the distributive law can actually make your multiplication process faster. In fact, the GMAT expects you to apply such techniques from high-school Math than to just perform multiplication by brute-force.
As per the distributive law, a(b+c) = ab + ac; also, a(b-c) = ab – ac.
These two versions are immensely useful for speeding up calculations, especially if you have built up the mindset to observe numbers, as we had mentioned in the first two parts.
Let’s take a few examples to understand better.
Example 1: Multiply 45 * 30.
45 * 30 = (40 + 5) * 30 = 40 * 30 + 5 * 30 = 1200 + 150 = 1350
Example 2: Multiply 15 with 13.8
15 (13.8) = 15 (14 – 0.2) = 15 (10 + 4 – 0.2) = 15 * 10 + 15 * 4 – 15 * 0.2 = 150 + 60 – 3 = 207.
Example 3: Multiply 42 with 17
42 (17) = 42(10 + 5 + 2) = 420 + 210 + 84 = 714 (note how it’s easy to find 42 * 5 if you know 42 * 10. GMAT expects you to do such smart calculations)
It can also be done by distributing the 42 while keeping the 17 constant.
17(42) = 17(40 + 2) = 680 + 34 = 714.
Therefore, flexibility is the biggest advantage of using the Distributive law. Based on your knowledge of multiplication tables, you can choose to break up the numbers that can help you multiply easily and quickly, rather than having to be one-dimensional.
And that’s the reason why we have put this method ahead of a couple of other speed math methods, in this article. If you know how to leverage the distributive law, you can make better use of the other two methods that we are going to describe now. These are:
- 1) Single line method
2) Base method
Each of these methods have their own advantages as well as limitations. While the single line method is broader in its application, the base method is more specific in where it can be applied. As such, the single line method requires consistent practice for a higher duration of time.
So, let’s look at both of these methods, one by one.
Single line method:
The single line method is so called because the final product is obtained in a single line, however big/small the multiplicands (the numbers being multiplied are known as multiplicands) are, unlike the conventional methods where we have rows and rows of numbers as the digits in the multiplicands increase.
Let's take an example where we try to multiply, say 43 with 37.
Step 1: Multiply the respective unit digits, 3 and 7 to get 21. We put the 1 as the unit digit of the result and take 2 as the carryover
Attachment:
SLM Step 1 Ex 1.JPG [ 11.34 KiB | Viewed 2808 times ]
Step 2: Cross multiply the units digit and the tens digit of each number and add the result. Do not forget to add the 2 that was carried over from the previous step. The unit digit of the result is taken and the rest is carried over.
Therefore, the result of this step = 7*4 + 3* 3 + 2 = 39
Attachment:
SLM Step 2 Ex 1.JPG [ 12.88 KiB | Viewed 2817 times ]
Step 3: Lastly, multiply the respective tens digits and add the number carried over from the previous step. The result will represent the remaining digits of the product.
In this case, multiply 4 with 3 to obtain 12 and add the carryover of 3 to get 15.
Attachment:
SLM Step 3 Ex 1.JPG [ 10.17 KiB | Viewed 2801 times ]
Now, you can go ahead and cross-verify if your answer is right 😊.
Let’s take another example to consolidate our learnings. Let’s try to multiply 57 with 29.
Attachment:
SLM Ex 2.JPG [ 26.94 KiB | Viewed 2786 times ]
Now that you have understood this method well, go ahead and take a few random two-digit numbers and practice this method till you get comfortable with it.
Base Method
As mentioned earlier, the base method can only be applied with specific numbers. However, it is a very powerful method in cases where it can be applied. It’s very simple to understand, practice and actually apply when needed.
The base method is applied when two numbers are very close to a reference number, which can typically be numbers like 10, 50, 100 and so on.
Let’s take an example to understand how it works. Let's try to multiply 15 with 16 (these are easy numbers to multiply even with the conventional method so that you may cross verify your answer)
Since 15 and 16 are both close to the number 10, the base for this calculation is 10.
Step 1: 15 – 10 = 5 and 16 – 10 = 6. . We arrange the numbers as shown below:
Attachment:
BM Step 1 Ex 1.JPG [ 8.95 KiB | Viewed 2826 times ]
The 5 and 6 here are the respective distances of 15 and 16 from the base, 10.
Step 2: We add the numbers in the direction of the arrows to get 21 in both cases. This is followed by multiplying this resultant number with the base
Since the base is 10, we multiply 21 with 10 to obtain 210 which is the result of this step
Attachment:
BM Step 2 Ex 1.JPG [ 11.81 KiB | Viewed 2791 times ]
Step 3: We multiply the numbers in the direction of the arrow and add it to the result of the previous step. The final sum represents the product of the given numbers.
Attachment:
BM Step 3 Ex 1.JPG [ 12.93 KiB | Viewed 2793 times ]
Let’s take another example, which represents a variation. If we have to multiply 23 * 18. We see that both numbers are close to the number 20; therefore, the base for this calculation is 20.
Let’s arrange the numbers as we did in the previous case:
Attachment:
BM Step 1 Ex 2.JPG [ 8.98 KiB | Viewed 2789 times ]
The 3 and -2 here are the respective distances of 23 and 18 from the base, 20. (Note that the distance of 18 from 20 is -2 since 18 is smaller. This is a convention followed in this method)
We add the numbers in the direction of the arrows to get 21 in both cases. Note that adding -2 to 23 gives 21. Since the base is 20, we multiply 21 with 20 to obtain 420 which is the result of this step
Attachment:
BM Step 2 Ex 2.JPG [ 12.59 KiB | Viewed 2796 times ]
We multiply the numbers in the direction of the arrow and add it to the result of the previous step
Attachment:
BM Step 3 Ex 2.JPG [ 12.65 KiB | Viewed 2759 times ]
- This is the advantage of this method that it only involves a small modification in Step 2 to accommodate for the base being a number other than 10.
The disadvantage of this method, of course, is that it can only be employed when both the numbers being multiplied are close to one common number. If this is not happening, then you will have to fall back on the Single line method.
We hope that this method is clear to you now. As always, go ahead and take some examples of your own and try to get comfortable with this method to the extent that you will start using it in your calculations.
With this, we conclude the third part of this article on smart calculations. In the fourth part of this article, tomorrow, we will be discussing methods to calculate squares and cubes of two-digit numbers.
Goodbye!
Kudos
Bookmarks
In the first three parts of this article we highlighted the importance of smart calculations and also discussed some smart methods for quick addition, subtraction and multiplication.
In case you have not had a look at it yet, click on the following links to check them out:
Smart calculations - Part 1
Smart calculations - Part 2
Smart calculations - Part 3
In the fourth part of this article, we shall discuss methods to quickly compute the squares and cubes of two-digit numbers. Although GMAT does not expect you to compute, say the square of 97, learning these methods will help you deal with the squares and cubes of smaller numbers with great ease. More importantly, they will continue to have an impact on your observation and inference skills and ultimately on your confidence, as we have been mentioning throughout this article.
On this note, let us take a look at some simple but effective methods to compute squares of two-digit numbers.
Squaring numbers ending with Zero
We shall start with the easiest of the two-digit numbers – numbers like 10, 20 etc., those ending with zero.
Squaring a number ending with zero is a very simple process, as most of you realize.
If x0 is a two digit number, where x is the tens digit, the last two digits of the square of x0 will be zeroes; the remaining digits can be obtained by squaring x.
That is, \((x0)^2\) = (\(x^2\))00
Note that the brackets on the RHS do not mean that we are multiplying \(x^2\) with 00.
For example, \((40)^2\) = 1600; here, the last two digits are zeroes and the 16 is the square of 4, which is the tens digit of 40.
Similarly, \((50)^2\) = 2500.
Note that this method can be applied on three digit numbers as well. For example, \((130)^2\) = 16900, the 169 being the square of 13.
Squaring numbers ending with 5
This method is not too difficult to understand either. This method is used to compute the squares of numbers ending with 5, numbers like 15, 25, 35 etc.
If (x5) is a number ending with 5, such that x represents the remaining digits of the numbers,
\((x5)^2\) = x(x+1)25.
Again, note that the brackets on the RHS do not mean that we are multiplying \(x(x+1)\) with 25.
On the contrary, it means that the last two digits of the square of a number ending with 5 will always be 25 (this is something we have discussed in detail in our article on Perfect squares and cubes, which you can access using this link Perfect Squares & Cubes ); the remaining digits of the square will be represented by x(x+1).
Let’s take some examples:
\((15)^2\) = 1(1+1) | 25 = 2 | 25 = 225
\((25)^2\) = 2(2+1) | 25 = 6 | 25 = 625
\((35)^2\) = 3(3+1) | 25 = 12 | 25 = 1225
Now, go ahead and find out the squares of numbers from 45 to 95, you will be able to do it in a matter of a couple of minutes.
Note that this method can also be extended to three-digit numbers, without having to make any change.
For example, \((125)^2\) = 12(12+1) | 25 = 156 | 25 = 15625
Squaring numbers ending with digits other than 5 and 0
For numbers ending with digits other than 5 and 0, we try to leverage our ability to calculate the squares of numbers ending with 5 /0.
Let’s take an example to understand. If we have to compute \(36^2\), it can be done very easily if we know \(35^2\); of course, we have already seen how to compute this.
So, \((36)^2\) = \((35)^2\) + 35 + 36 = 1225 + 71 = 1296.
We can follow a similar approach for numbers ending with digits closer to 0.
For example, \((41)^2\) = \((40)^2\) + 40 + 41 = 1600 + 81 = 1681.
If we need to calculate the square of, say 39, we flip this process around and subtract instead of adding.
So, \(39^2\) = \(40^2\) - 40 - 39 = 1600 - 79 = 1521.
Of course, as we mentioned at the start of this article, the possibility that GMAT will expect you to compute the square of a number greater than 40 is remote. Hence, you will have to learn to apply these methods on smaller numbers, which can be done fairly easily.
Computing Perfect cubes of two-digit numbers
We would like to start off by saying that this method is an add-on for you, along with the methods that have been described in the various parts of this article. GMAT will never expect you to compute the cubes of numbers bigger than, say 20.
As such, if you wish to skip this technique, you can do so. However, if you don’t mind having an additional weapon in your arsenal, read on (who knows, this might just come in handy in a question on Compound Interest)
The method to calculate the cube of a two-digit number involves multiple steps, hence please pay attention to the description of each step and perform them meticulously during your attempts.
Let’s say the two digit number is (ab).
1. Step 1, which is probably the most important step in this method is to cube the tens digit of the given number i.e. to compute \(a^3\).
2. Once this is done, we will write down 4 numbers in a straight line such that any 2 numbers bear the ratio of a:b
3. In the next step, we double the numbers in the middle of the top row and write them below these numbers.
4. Finally, we add the numbers, one column at a time.
Example 1: Compute \(14^3\)
Cubing the tens digit of 14, we have \(1^3\) = 1. Now, starting with this 1, we write down four number such that any 2 numbers bear the ratio of 1:4, which is the ratio of the digits of the number 14. After this, we double the two numbers in the middle and finally add the numbers, one column at a time, to obtain the cube of 14 as 2744
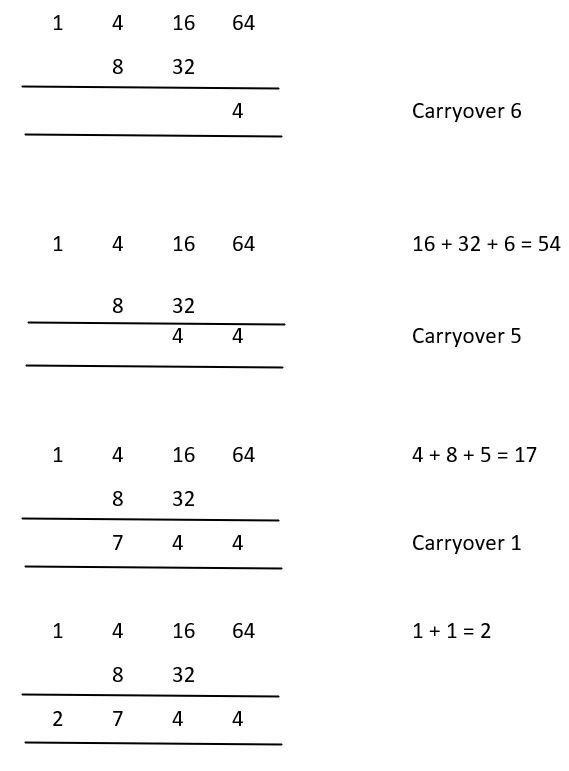
Cubing Ex 1.JPG [ 34.69 KiB | Viewed 2774 times ]
Example 2: Compute \(23^3\)
Cubing the tens digit of 22, we have \(2^3\) = 8. Now, starting with this 8, we write down four number such that any 2 numbers bear the ratio of 2:3, which is the ratio of the digits of the number 23. After this, we double the two numbers in the middle and finally add the numbers, one column at a time, to obtain the cube of 23 as 12167.

Cubing Ex 2.JPG [ 32.46 KiB | Viewed 2759 times ]
This brings us to the end of the fourth part of this article on smart calculations. In the fifth and final part tomorrow, we will look at how fractions can be leveraged to quickly solve percentage related questions.
We hope that you have been practicing some of these methods from this article, over the last few days. Keep at it and in a few more days, you will be a natural at these methods and hence, you will start implementing them when practicing GMAT quant questions.
Goodbye!
In case you have not had a look at it yet, click on the following links to check them out:
Smart calculations - Part 1
Smart calculations - Part 2
Smart calculations - Part 3
In the fourth part of this article, we shall discuss methods to quickly compute the squares and cubes of two-digit numbers. Although GMAT does not expect you to compute, say the square of 97, learning these methods will help you deal with the squares and cubes of smaller numbers with great ease. More importantly, they will continue to have an impact on your observation and inference skills and ultimately on your confidence, as we have been mentioning throughout this article.
On this note, let us take a look at some simple but effective methods to compute squares of two-digit numbers.
Squaring numbers ending with Zero
We shall start with the easiest of the two-digit numbers – numbers like 10, 20 etc., those ending with zero.
Squaring a number ending with zero is a very simple process, as most of you realize.
If x0 is a two digit number, where x is the tens digit, the last two digits of the square of x0 will be zeroes; the remaining digits can be obtained by squaring x.
That is, \((x0)^2\) = (\(x^2\))00
Note that the brackets on the RHS do not mean that we are multiplying \(x^2\) with 00.
For example, \((40)^2\) = 1600; here, the last two digits are zeroes and the 16 is the square of 4, which is the tens digit of 40.
Similarly, \((50)^2\) = 2500.
Note that this method can be applied on three digit numbers as well. For example, \((130)^2\) = 16900, the 169 being the square of 13.
Squaring numbers ending with 5
This method is not too difficult to understand either. This method is used to compute the squares of numbers ending with 5, numbers like 15, 25, 35 etc.
If (x5) is a number ending with 5, such that x represents the remaining digits of the numbers,
\((x5)^2\) = x(x+1)25.
Again, note that the brackets on the RHS do not mean that we are multiplying \(x(x+1)\) with 25.
On the contrary, it means that the last two digits of the square of a number ending with 5 will always be 25 (this is something we have discussed in detail in our article on Perfect squares and cubes, which you can access using this link Perfect Squares & Cubes ); the remaining digits of the square will be represented by x(x+1).
Let’s take some examples:
\((15)^2\) = 1(1+1) | 25 = 2 | 25 = 225
\((25)^2\) = 2(2+1) | 25 = 6 | 25 = 625
\((35)^2\) = 3(3+1) | 25 = 12 | 25 = 1225
Now, go ahead and find out the squares of numbers from 45 to 95, you will be able to do it in a matter of a couple of minutes.
Note that this method can also be extended to three-digit numbers, without having to make any change.
For example, \((125)^2\) = 12(12+1) | 25 = 156 | 25 = 15625
Squaring numbers ending with digits other than 5 and 0
For numbers ending with digits other than 5 and 0, we try to leverage our ability to calculate the squares of numbers ending with 5 /0.
Let’s take an example to understand. If we have to compute \(36^2\), it can be done very easily if we know \(35^2\); of course, we have already seen how to compute this.
So, \((36)^2\) = \((35)^2\) + 35 + 36 = 1225 + 71 = 1296.
We can follow a similar approach for numbers ending with digits closer to 0.
For example, \((41)^2\) = \((40)^2\) + 40 + 41 = 1600 + 81 = 1681.
If we need to calculate the square of, say 39, we flip this process around and subtract instead of adding.
So, \(39^2\) = \(40^2\) - 40 - 39 = 1600 - 79 = 1521.
Of course, as we mentioned at the start of this article, the possibility that GMAT will expect you to compute the square of a number greater than 40 is remote. Hence, you will have to learn to apply these methods on smaller numbers, which can be done fairly easily.
Computing Perfect cubes of two-digit numbers
We would like to start off by saying that this method is an add-on for you, along with the methods that have been described in the various parts of this article. GMAT will never expect you to compute the cubes of numbers bigger than, say 20.
As such, if you wish to skip this technique, you can do so. However, if you don’t mind having an additional weapon in your arsenal, read on (who knows, this might just come in handy in a question on Compound Interest)
The method to calculate the cube of a two-digit number involves multiple steps, hence please pay attention to the description of each step and perform them meticulously during your attempts.
Let’s say the two digit number is (ab).
1. Step 1, which is probably the most important step in this method is to cube the tens digit of the given number i.e. to compute \(a^3\).
2. Once this is done, we will write down 4 numbers in a straight line such that any 2 numbers bear the ratio of a:b
3. In the next step, we double the numbers in the middle of the top row and write them below these numbers.
4. Finally, we add the numbers, one column at a time.
Example 1: Compute \(14^3\)
Cubing the tens digit of 14, we have \(1^3\) = 1. Now, starting with this 1, we write down four number such that any 2 numbers bear the ratio of 1:4, which is the ratio of the digits of the number 14. After this, we double the two numbers in the middle and finally add the numbers, one column at a time, to obtain the cube of 14 as 2744
Attachment:
Cubing Ex 1.JPG [ 34.69 KiB | Viewed 2774 times ]
Example 2: Compute \(23^3\)
Cubing the tens digit of 22, we have \(2^3\) = 8. Now, starting with this 8, we write down four number such that any 2 numbers bear the ratio of 2:3, which is the ratio of the digits of the number 23. After this, we double the two numbers in the middle and finally add the numbers, one column at a time, to obtain the cube of 23 as 12167.
Attachment:
Cubing Ex 2.JPG [ 32.46 KiB | Viewed 2759 times ]
This brings us to the end of the fourth part of this article on smart calculations. In the fifth and final part tomorrow, we will look at how fractions can be leveraged to quickly solve percentage related questions.
We hope that you have been practicing some of these methods from this article, over the last few days. Keep at it and in a few more days, you will be a natural at these methods and hence, you will start implementing them when practicing GMAT quant questions.
Goodbye!







