|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Kudos
Bookmarks
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
(N/A)
Question Stats:
0% (00:00) correct 0% (00:00) wrong
0% (00:00) wrong  based on 0 sessions
based on 0 sessions
History
Date
Time
Result
Not Attempted Yet
A pizza restaurant has 2 choices of crust: deep dish crust or thin crust. The restaurant also has a choice of 5 toppings: tomatoes, sausage, peppers, onions, and pepperoni. The order of the toppings doesn’t matter. Finally, the restaurant offers every pizza in extra cheese as well as regular. If someone orders a pizza with 4 unique toppings, how many different combinations are possible for the toppings?
Kudos
Bookmarks
OE
Set up 4 slots for the toppings and label all the slots the same, since order doesn’t matter. Fill in the numbers from 5 on down, because the person orders 4 unique toppings.
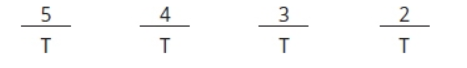
Now multiply the numbers and divide by 4! because the labels are all the same.
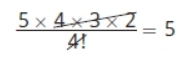
Alternatively, use the combinations formula to count the combinations of toppings:

Or use an intuitive approach: choosing 4 toppings out of 5 is equivalent to choosing the 1 topping that will not be on the pizza. There are only 5 ways to reject a single topping.
Next, since each of these pizzas can also be offered in 2 choices of crust, there are 5 × 2 = 10 possible pizzas with 4 unique toppings and one of the two crusts.
The same logic applies for extra cheese and regular. The number of pizzas with 4 toppings, one crust, and one version of cheese is 5 × 2 × 2 = 20.
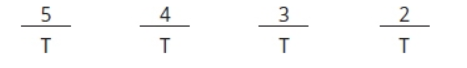
GMAT-Club-Forum-t8gojh43.png [ 7.46 KiB | Viewed 86 times ]
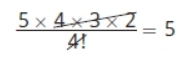
GMAT-Club-Forum-eznom4zr.png [ 8.26 KiB | Viewed 87 times ]

GMAT-Club-Forum-4633l2tk.png [ 5.56 KiB | Viewed 85 times ]
Set up 4 slots for the toppings and label all the slots the same, since order doesn’t matter. Fill in the numbers from 5 on down, because the person orders 4 unique toppings.
Now multiply the numbers and divide by 4! because the labels are all the same.
Alternatively, use the combinations formula to count the combinations of toppings:
Or use an intuitive approach: choosing 4 toppings out of 5 is equivalent to choosing the 1 topping that will not be on the pizza. There are only 5 ways to reject a single topping.
Next, since each of these pizzas can also be offered in 2 choices of crust, there are 5 × 2 = 10 possible pizzas with 4 unique toppings and one of the two crusts.
The same logic applies for extra cheese and regular. The number of pizzas with 4 toppings, one crust, and one version of cheese is 5 × 2 × 2 = 20.
Attachment:
GMAT-Club-Forum-t8gojh43.png [ 7.46 KiB | Viewed 86 times ]
Attachment:
GMAT-Club-Forum-eznom4zr.png [ 8.26 KiB | Viewed 87 times ]
Attachment:
GMAT-Club-Forum-4633l2tk.png [ 5.56 KiB | Viewed 85 times ]








