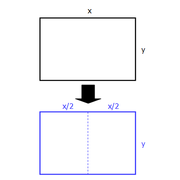
A project requires a rectangular sheet of cardboard satisfying the fol

The first and the foremost thing to realize is that one side of the figure would be cut by half. Now when you go through the options, please make sure on thing. There is no need to half the smaller side in the option, as it would be the total waste of time. For example, if you have a rectangular figure with a ratio of 1:4, then halfing the smaller side would bring the ration to .5 to 4, which means that the ratio will decrease further rather than remaining the same.

So now let's go to the option choices:
a) Sheet measuring 7*10 : Lets half the larger side"10", we get 7:5, now is 5/7 equal to 7/10. I would say pretty close- lets keep.
b) A sheet measuring 8 inches by 14 inches: Half the larger side we get, 7/8 vs 8/14: No chance of being close- eliminate
c) A sheet measuring 10 inches by 13 inches: Half the larger side we get, 6.5/10 vs 10/13: Not close- eliminate
d) A sheet measuring 3 feet by 5 feet: 2.5/3 vs 3/5 : No chance
e) A sheet measuring 5 feet by 8 feet: 4/5 vs 5/8: Not close

Your answer is A

Hi Brent a lil basic question : While trying to maintain the ratio of the new triangle to the Original Triangle why did you reverse the side . SHould the Sides of both the triangles not corelate that is height / width vs Height / width ie x/y ( Old ratio ) = (x/2 )/ y ( new ratio ) ?

in the solution provided by you you have done the following
" In other words, we want x/y = y/(x/2)
Cross multiply to get: x²/2 = y² ''

PLease explain

Do the math. OR print thousands of documents in letter (7x11) and tabloid (11x14) sizes and KNOW that when you fold a tabloid in half you get 2 letter sizes. Closest to these dimensions is 7x10 HENCE A.

Posted from my mobile device

An easy method to do this would be -

a) 7/10, 5/7, now multiply the denominator with the numerator and see which numbers are closest. so, in this case, 49 , 50
b) 4/7, 7/8 =>32, 49
c) 10/13, 13/20 . 200, 169
d) 3/5, 5/6. 18, 15
e) 5/8, 4/5. 25, 32

As you can see that A is closest, so you dont have to approximate the values in this.

Hi mimajit,

The question you have asked is actually the key to getting the question correct. If you observe the diagram from Brent's post then x is the longer side and y is the shorter side of the rectangle. And we know that in a rectangle the length is the longer side and the width is the shorter side.

When we slice the rectangle into two halves x divides into two \(\frac{x}{2}\)'s and now \(\frac{x}{2}\) no longer remains the longer side and it is y that becomes the length now. Hence, when we take the ratio of length by width y becomes the length and \(\frac{x}{2}\) becomes the width.

As a side note, if you continue to keep \(\frac{x}{2}\) as the length then you will end up with a tautology - \(\frac{x}{y} = \frac{x}{2y}\) where \(\frac{x}{y}\) cancel out on both sides.

Warm Regards,
Pritish

Official Explanation:

There are two possible approaches to this problem: algebra and working backwards from the answer choices. Both solutions are given below.

Algebraic Solution:
Say the original sheet measures L by W, with L > W, so that the cut yields two rectangular halves measuring L/2 by W each.
Per the project requirements, the ratio of these new dimensions must be the same as the ratio of L to W. Consider both possible ways in which the ratio might be set up. If the ratio of original to new is set up as L : W = L/2 : W, then it reduces to 1 = 1/2, an impossible condition. (Or, if you prefer to reason theoretically, it is impossible to reduce L by half but leave W unchanged and have the ratio stay the same.)

Therefore, the width (W) of the original rectangle, must become the longer side for the smaller rectangles. The ratio must be set up as L : W = W : L/2.

Set up the ratio:
W/\(\frac{L}{2}\)=\(\frac{L}{W}\)
\(W^2\)=\(\frac{L^2}{2}\)
\(2W^2=L^2\)
\(W√2=L\)
The condition thus requires original dimensions that come as close as possible to satisfying \(W√2=L\), or, equivalently,\(\frac{L}{W}=√2\).
The square root of 2 is approximately 1.4 (if you don’t already have this memorized, memorize it right now!). The answer choices represent the size of the original sheet (before being cut); call the larger dimension L and the smaller one W. Use the answer choices to calculate an approximate value for L/W. The one closest to 1.4 is the correct answer.

(A) 10/7 = approximately 1.4
(B) 14/8 = 7/4 = 1.75
(C) 13/10 = 1.3
(D) 5/3 = approximately 1.7
(E) 8/5 = 1.6
Choice A comes closest to the requirement. The correct answer is (A).


Working Backwards:
As shown at the beginning of the algebraic solution, when the paper is cut in half, what used to be the width becomes the length of the smaller rectangles. In other words, in order for the original ratio to equal the new one, \(L : W = W : \frac{L}{2.}\)
Starting from the answer choices, test the requirement directly. First, find the ratio of the original dimensions (\(\frac{L}{W}\)). Then, find the ratio of the dimensions after one dimension (the longer one) is cut in half; this will be W/\(\frac{L}{2}\). The correct answer is the choice for which the two ratios are closest to being equal.

(A) The original ratio is 10/7. Half of 10 is 5, so the new dimensions are 7 and 5. The ratio for each smaller rectangle is 7/5 = 14/10. (Remember to use the larger number as the numerator, as you did in the original ratio.) Find a common denominator to compare the ratios: 100/70 and 98/70. Pretty close!

(B) The original ratio is 14/8. Half of 14 is 7, so the ratio for each smaller rectangle is 8/7. Find a common denominator to compare the ratios (but make your life easier: simplify 14/8 to 7/4): 49/28 and 32/28. These are not as close as the ratios in answer (A), so eliminate (B).

(C) The original ratio is 13/10. Half of 13 is 6.5, so the ratio for each smaller rectangle is 10/6.5 = 20/13. Find a common denominator to compare the ratios: 169/130 and 200/130. These are not as close as the ratios in answer (A), so eliminate (C).

(D) The original ratio is 5/3. Half of 5 is 2.5, so the ratio for each smaller rectangle is 3/2.5 = 6/5. Find a common denominator to compare the ratios: 25/15 and 18/15. These are not as close as the ratios in answer (A), so eliminate (D).

(E) The original ratio is 8/5. Half of 8 is 4, so the ratio for each smaller rectangle is 5/4. Find a common denominator to compare the ratios: 32/20 and 25/20. These are not as close as the ratios in answer (A), so eliminate (E).
The correct answer is (A).

Bunuel requesting you approach for solving this question.
I did not understand why the solution posted above have considered length cut to half and not width. Or it doesn't matter

Hello from the GMAT Club BumpBot!

Thanks to another GMAT Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).

Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.