Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
11:00 AM EST
-11:59 PM EST
Don’t miss Target Test Prep’s biggest sale of the year! Grab 25% off any Target Test Prep GMAT plan during our Black Friday sale. Just enter the coupon code BLACKFRIDAY25 at checkout to save up to $625. - Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 22
12:00 PM PST
-12:30 PM PST
olve GRE practice problems covering Quantitative reasoning, Verbal Reasoning, Text Completion, Sentence Equivalence, and Reading Comprehension Problems. Take this GRE practice quiz live with peers, analyze your GRE study progress, - Nov 23
10:00 AM PST
-11:00 AM PST
GMAT practice session and solve 30 challenging GMAT questions with other test takers in timed conditions, covering GMAT Quant, Data Sufficiency, Data Insights, Reading Comprehension, and Critical Reasoning questions. - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 30
10:00 AM EST
-11:59 PM EST
Get $325 off the TTP OnDemand GMAT masterclass by using the coupon code BLACKFRIDAY25 at checkout. If you prefer learning through engaging video lessons, TTP OnDemand GMAT is exactly what you need.
Kudos
Bookmarks
A
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
 75%
(hard)
75%
(hard)
Question Stats:
57% (02:18) correct 43%
(02:25)
wrong
43%
(02:25)
wrong  based on 377
sessions
based on 377
sessions
History
Date
Time
Result
Not Attempted Yet
A school has 3 classes, math class has 14 students. English class has 10 students, PE class has 11 students. There are 20 students taking only one class, 3 students are taking all three classes. How many students are taking two classes?
A) 3
B) 6
C) 9
D) 18
E)20
could any one show me the solution using 3 overlapping groups formula .
T = A + B + C - (AB + AC + BC) - 2(ABC) ... I am getting a wrong answer
thanks !
A) 3
B) 6
C) 9
D) 18
E)20
could any one show me the solution using 3 overlapping groups formula .
T = A + B + C - (AB + AC + BC) - 2(ABC) ... I am getting a wrong answer
thanks !
Kudos
Bookmarks
This could be solved easier:
(1) There are 14+10+11 = 35 seats to fill (some students occupy only 1 seat, others 2, others 3).
(2) 20 students occupy only 1 seat: 35-20 = 15... now we have 15 seats to fill
(3) 3 students occupy 3 seats: 15-9 = 6 seats left
(4) We have 6 seats for students that occupy 2 seats ---> solution is 3 students!!
Answer A
(1) There are 14+10+11 = 35 seats to fill (some students occupy only 1 seat, others 2, others 3).
(2) 20 students occupy only 1 seat: 35-20 = 15... now we have 15 seats to fill
(3) 3 students occupy 3 seats: 15-9 = 6 seats left
(4) We have 6 seats for students that occupy 2 seats ---> solution is 3 students!!
Answer A
Kudos
Bookmarks
If we put up a Venn diagram of the situation, we get something like this :
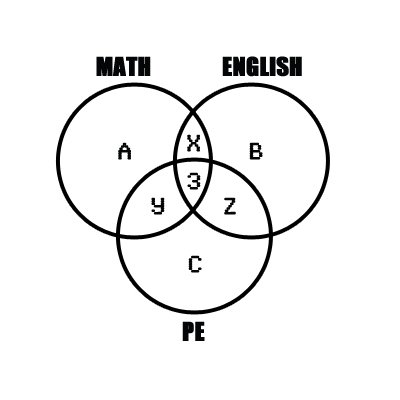
venn.jpg [ 55.63 KiB | Viewed 11023 times ]
With :
A : the number of students only attending math class ;
B : the number of students only attending english class ;
C : the number of students only attending PE class ;
x : the number of students attending both math and english ;
y : the number of students attending both math and PE ;
z : the number of students attending both english and PE.
If we use the data we're given, we get the following system :
14 students attend math classes => \(x + y + 3 + A = 14\) (1)
10 students attend english classes => \(x + z + 3 + B = 10\) (2)
11 students attend PE classes =>\(y + z + 3 + C = 11\) (3)
We also know that there are only 20 students attending only one class, which means that : \(A + B + C = 20\) (4)
If we add equations (1), (2) and (3) and take into account equation (4) we get : \(2*(x + y + z) + 9 + 20 =35\)
The quantity \((x + y + z)\) represents the total number of students attending 2 classes, which is what we're looking for. So completing the computation, we get :
\(2*(x + y + z) + 9 + 20 =35\) => \(2*(x + y + z) = 6\) => \((x + y + z) = 3\) which is answer choice A.
Hope that helped
Attachment:
venn.jpg [ 55.63 KiB | Viewed 11023 times ]
A : the number of students only attending math class ;
B : the number of students only attending english class ;
C : the number of students only attending PE class ;
x : the number of students attending both math and english ;
y : the number of students attending both math and PE ;
z : the number of students attending both english and PE.
If we use the data we're given, we get the following system :
14 students attend math classes => \(x + y + 3 + A = 14\) (1)
10 students attend english classes => \(x + z + 3 + B = 10\) (2)
11 students attend PE classes =>\(y + z + 3 + C = 11\) (3)
We also know that there are only 20 students attending only one class, which means that : \(A + B + C = 20\) (4)
If we add equations (1), (2) and (3) and take into account equation (4) we get : \(2*(x + y + z) + 9 + 20 =35\)
The quantity \((x + y + z)\) represents the total number of students attending 2 classes, which is what we're looking for. So completing the computation, we get :
\(2*(x + y + z) + 9 + 20 =35\) => \(2*(x + y + z) = 6\) => \((x + y + z) = 3\) which is answer choice A.
Hope that helped











