Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Fish181
Joined: 13 Dec 2023
Last visit: 22 Jan 2025
Posts: 135
Given Kudos: 53
Status:Applying in R1 of 2024 to t15
Affiliations: University of Tennessee
Location: United States (CO)
Concentration: Strategy, Finance
GMAT Focus 1: 605 Q76 V84 DI80 

GMAT Focus 2: 615 Q78 V86 DI78 

GPA: 3.62
WE:Analyst (Consumer Packaged Goods)
GMAT Focus 2: 615 Q78 V86 DI78 

Posts: 135
Runner D will be awarded the $50 prize.: No
Runner A will be awarded the $30 prize.: No
Both prizes will be awarded to the same Individual: Yes
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
 95%
(hard)
95%
(hard)
Question Stats:
48% (02:59) correct 52%
(02:59)
wrong
52%
(02:59)
wrong  based on 1133
sessions
based on 1133
sessions
History
Date
Time
Result
Not Attempted Yet
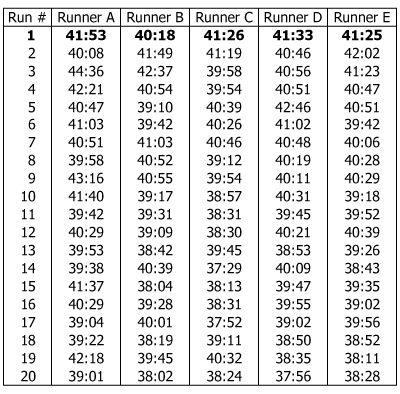
Five amateur runners are competing with one another during a series of 20 designated 10 km training runs. A prize of $50 will be awarded to the runner with the overall fastest time (the fastest among all of the times in all of the runs), and a prize of $30 to the runner with the individual time that shows the greatest improvement (decrease in time) from that runner's time for the first of the designated runs. The times are shown in the table in minutes and seconds. The times for the first run are shown in boldface.
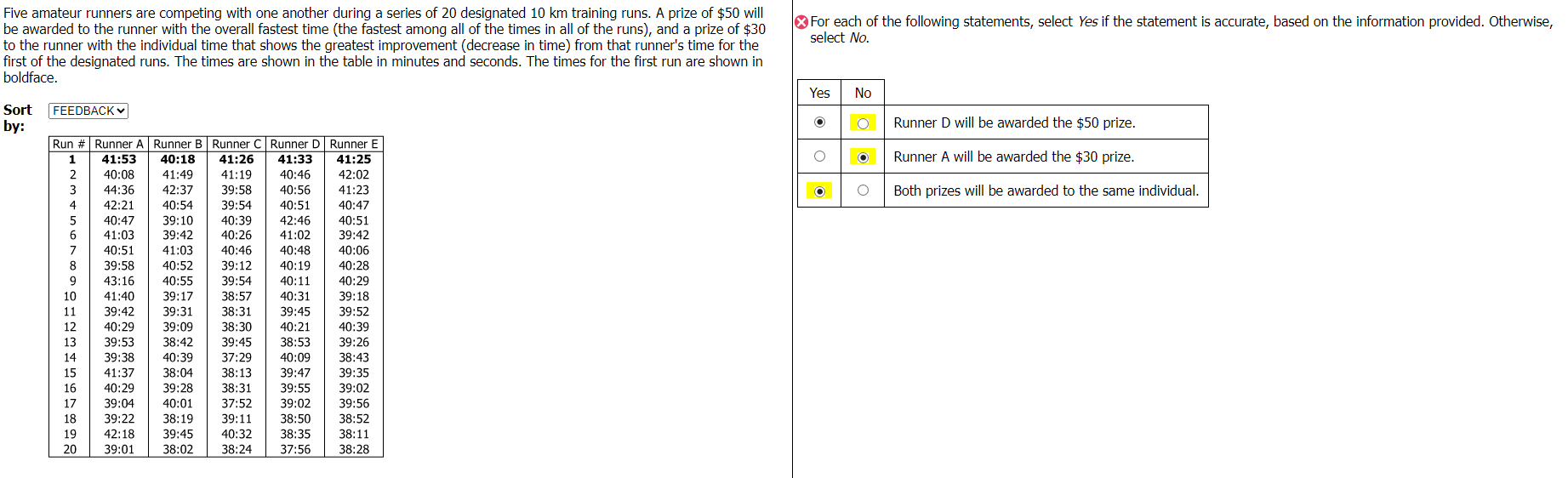
For each of the following statements, select Yes if the statement is accurate, based on the information provided. Otherwise, select No.
GMAT-Club-Forum-s2zm6xpz.png [ 36.16 KiB | Viewed 3281 times ]
GMAT-Club-Forum-bmnkddu2.png [ 99.86 KiB | Viewed 3277 times ]
| Run # | Runner A | Runner B | Runner C | Runner D | Runner E |
|---|---|---|---|---|---|
| 1 | ‘41:53 | ‘40:18 | ‘41:26 | ‘41:33 | ‘41:25 |
| 2 | ‘40:08 | ‘41:49 | ‘41:19 | ‘40:46 | ‘42:02 |
| 3 | ‘44:36 | ‘42:37 | ‘39:58 | ‘40:56 | ‘41:23 |
| 4 | ‘42:21 | ‘40:54 | ‘39:54 | ‘40:51 | ‘40:47 |
| 5 | ‘40:47 | ‘39:10 | ‘40:39 | ‘42:46 | ‘40:51 |
| 6 | ‘41:03 | ‘39:42 | ‘40:26 | ‘41:02 | ‘39:42 |
| 7 | ‘40:51 | ‘41:03 | ‘40:46 | ‘40:48 | ‘40:06 |
| 8 | ‘39:58 | ‘40:52 | ‘39:12 | ‘40:19 | ‘40:28 |
| 9 | ‘43:16 | ‘40:55 | ‘39:54 | ‘40:11 | ‘40:29 |
| 10 | ‘41:40 | ‘39:17 | ‘38:57 | ‘40:31 | ‘39:18 |
| 11 | ‘39:42 | ‘39:31 | ‘38:31 | ‘39:45 | ‘39:52 |
| 12 | ‘40:29 | ‘39:09 | ‘38:30 | ‘40:21 | ‘40:39 |
| 13 | ‘39:53 | ‘38:42 | ‘39:45 | ‘38:53 | ‘39:26 |
| 14 | ‘39:38 | ‘40:39 | ‘37:29 | ‘40:09 | ‘38:43 |
| 15 | ‘41:37 | ‘38:04 | ‘38:13 | ‘39:47 | ‘39:35 |
| 16 | ‘40:29 | ‘39:28 | ‘38:31 | ‘39:55 | ‘39:02 |
| 17 | ‘39:04 | ‘40:01 | ‘37:52 | ‘39:02 | ‘39:56 |
| 18 | ‘39:22 | ‘38:19 | ‘39:11 | ‘38:50 | ‘38:52 |
| 19 | ‘42:18 | ‘39:45 | ‘40:32 | ‘38:35 | ‘38:11 |
| 20 | ‘39:01 | ‘38:02 | ‘38:24 | ‘37:56 | ‘38:28 |
For each of the following statements, select Yes if the statement is accurate, based on the information provided. Otherwise, select No.
Attachment:
GMAT-Club-Forum-s2zm6xpz.png [ 36.16 KiB | Viewed 3281 times ]
Attachment:
GMAT-Club-Forum-bmnkddu2.png [ 99.86 KiB | Viewed 3277 times ]
| Yes | No | |
| Runner D will be awarded the $50 prize. | ||
| Runner A will be awarded the $30 prize. | ||
| Both prizes will be awarded to the same Individual |
ShowHide Answer
Official Answer
Runner D will be awarded the $50 prize.: No
Runner A will be awarded the $30 prize.: No
Both prizes will be awarded to the same Individual: Yes
Kudos
Bookmarks
1. 50$ prize is awarded to the person with the fastest time.
Runner D's fastest time is 37:56, while Runner C's fastest time is 37:29. So the answer is no.
2. Runner A's time difference between his fastest and his first run is 41:53 - 39:01 = 2:52, while Runner C's time difference between first run and fastest run is 41:26 - 37:29 = 3:57. So the answer is No.
3. Runner C has fastest time, we must check if his improvement is also the best. From the previous question we can see that it is not A. B's beginning time is faster and his fastest time is slower --> less of a difference. D has a 5 second slower first running time but his fastest time is 27 seconds is also slower so the difference is smaller. E has a 1 second faster starting run but none of his runs break the 37 minute mark so his improvement will also be smaller. The answer is Yes.
Runner D's fastest time is 37:56, while Runner C's fastest time is 37:29. So the answer is no.
2. Runner A's time difference between his fastest and his first run is 41:53 - 39:01 = 2:52, while Runner C's time difference between first run and fastest run is 41:26 - 37:29 = 3:57. So the answer is No.
3. Runner C has fastest time, we must check if his improvement is also the best. From the previous question we can see that it is not A. B's beginning time is faster and his fastest time is slower --> less of a difference. D has a 5 second slower first running time but his fastest time is 27 seconds is also slower so the difference is smaller. E has a 1 second faster starting run but none of his runs break the 37 minute mark so his improvement will also be smaller. The answer is Yes.
Kudos
Bookmarks
Formatted the question and unlocked the topic. Fish181 could you please check whether the OAs put are correct?












