|
|
GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
14 Oct 2025, 10:40
Kudos
Bookmarks
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
(N/A)
Question Stats:
0% (00:00) correct
0% (00:00) wrong based on 0 sessions
History
Date
Time
Result
Not Attempted Yet
The following table shows the weekly spending of a small business on office supplies.
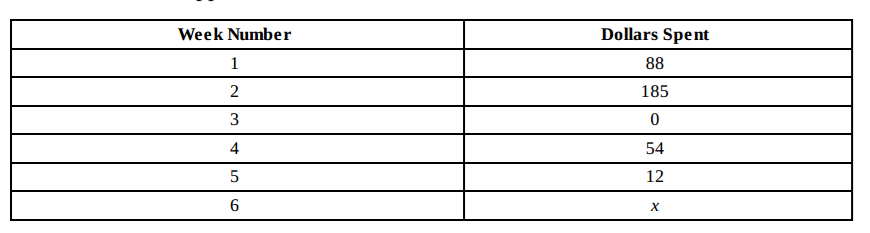
For what values of x are both the mean (average) and the median weekly spending for the entire period between 60 and 70 dollars?
Indicate all that apply.
A. 65
B. 72
C. 80
D. 83
E. 89
GMAT-Club-Forum-go4zarhj.png [ 12.16 KiB | Viewed 56 times ]
For what values of x are both the mean (average) and the median weekly spending for the entire period between 60 and 70 dollars?
Indicate all that apply.
A. 65
B. 72
C. 80
D. 83
E. 89
Attachment:
GMAT-Club-Forum-go4zarhj.png [ 12.16 KiB | Viewed 56 times ]
18 Oct 2025, 03:41
Kudos
Bookmarks
Official Explanation
Start by arranging the five known numbers in order from least to greatest: 0, 12, 54, 88, 185. If x > 88, then 54 and 88 become the two middle values, and the median
This is not between 60 and 70, so (E) is not correct.
If x = 65, choice (A), 54 and 65 become the two middle values, and the median
So (A) is not correct.
The average of six numbers will be between 60 and 70 when their sum, or total, is between 6 × 60 = 360 and 6 × 70 = 420. The sum of the weekly spending figures given is 0 + 12 + 54 + 88 + 185 + x = 339 + x. Then 360 < 339 + x < 420. Subtracting 339 from all three branches of the inequality yields 21 < x < 81. (D) is incorrect, because 83 > 81, so only choices (B) and (C) remain as correct.
Answer: B,C
GMAT-Club-Forum-uq36ewsp.png [ 14.97 KiB | Viewed 20 times ]
GMAT-Club-Forum-mbqvuq01.png [ 16.51 KiB | Viewed 21 times ]
Start by arranging the five known numbers in order from least to greatest: 0, 12, 54, 88, 185. If x > 88, then 54 and 88 become the two middle values, and the median
If x = 65, choice (A), 54 and 65 become the two middle values, and the median
So (A) is not correct.
The average of six numbers will be between 60 and 70 when their sum, or total, is between 6 × 60 = 360 and 6 × 70 = 420. The sum of the weekly spending figures given is 0 + 12 + 54 + 88 + 185 + x = 339 + x. Then 360 < 339 + x < 420. Subtracting 339 from all three branches of the inequality yields 21 < x < 81. (D) is incorrect, because 83 > 81, so only choices (B) and (C) remain as correct.
Answer: B,C
Attachment:
GMAT-Club-Forum-uq36ewsp.png [ 14.97 KiB | Viewed 20 times ]
Attachment:
GMAT-Club-Forum-mbqvuq01.png [ 16.51 KiB | Viewed 21 times ]
