Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth
Kudos
Bookmarks
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
(N/A)
Question Stats:
100% (00:06) correct 0% (00:00) wrong
0% (00:00) wrong  based on 1 sessions
based on 1 sessions
History
Date
Time
Result
Not Attempted Yet
From the menu above, a restaurant offers customers two choices of appetizer and one choice each of entrée and dessert. If the appetizers must be different from each other, how many different meal combinations are available to customers?
Attachment:
GMAT-Club-Forum-pyu7nmji.jpeg [ 45.1 KiB | Viewed 82 times ]
Kudos
Bookmarks
Official Explanation
Find the number of choices for appetizers with the “choose” function, written as and defined for positive integers by the formula
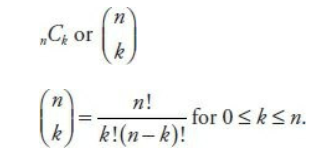
Recall that n! means the product of all positive integers from 1 through n, inclusive. From six appetizers, we choose two, so there are 6C2 combinations, which equals

after canceling duplicate numbers in the numerator and denominator. You can also compute this by “brute force.” Label the appetizers A, B, C, D, E, and F, and then list all combinations of two appetizers as follows: AB, AC, AD, AE, AF, BC, BD, BE, BF, CD, CE, CF, DE, DF, EF. There are 5 + 4 + 3 + 2 + 1 = 15 combinations in all. Multiply the number of choices for appetizer by the four choices for entrée and the five choices for dessert to obtain 15 × 4 × 5 = 300 total menu combinations.
Answer: 300
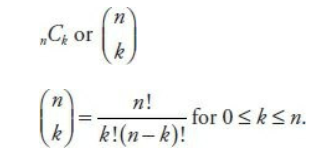
GMAT-Club-Forum-9iw8dncy.png [ 32.66 KiB | Viewed 51 times ]

GMAT-Club-Forum-4gk0g4gr.png [ 6.06 KiB | Viewed 53 times ]
Find the number of choices for appetizers with the “choose” function, written as and defined for positive integers by the formula
Recall that n! means the product of all positive integers from 1 through n, inclusive. From six appetizers, we choose two, so there are 6C2 combinations, which equals
after canceling duplicate numbers in the numerator and denominator. You can also compute this by “brute force.” Label the appetizers A, B, C, D, E, and F, and then list all combinations of two appetizers as follows: AB, AC, AD, AE, AF, BC, BD, BE, BF, CD, CE, CF, DE, DF, EF. There are 5 + 4 + 3 + 2 + 1 = 15 combinations in all. Multiply the number of choices for appetizer by the four choices for entrée and the five choices for dessert to obtain 15 × 4 × 5 = 300 total menu combinations.
Answer: 300
Attachment:
GMAT-Club-Forum-9iw8dncy.png [ 32.66 KiB | Viewed 51 times ]
Attachment:
GMAT-Club-Forum-4gk0g4gr.png [ 6.06 KiB | Viewed 53 times ]








