If point C were on the circumference of the circle, then we know from the concept of Inscribed Angles in a semi-circle that the Angle would be 90 degrees.
Start out with Point C on the circumference. This is a 90 degree angle.
Then, to get to the figure, just picture “flattening” or “dragging down” point C closer to the diameter of the circle.
This will result in the Angle at Vertex C becoming wider.
The Side of Length 6 that would fit the right triangle (6-8-10) would have to stay the same, but in order to accommodate this wider angle, the unknown side would have to shorten.———-> hence, we would have an obtuse triangle with one angle greater then 90 degrees and the unknown side will have to be shorter than the Leg of length 8 were the angle actually 90 degrees
Any triangle that has one angle greater than 90 degrees (there can only ever be one angle that is greater than 90 degrees) is an obtuse triangle
Now that you know the triangle must be an obtuse triangle, you can use the Property that
GMATinsight uses
For any obtuse triangle:
(Longest side)^2 > (shorter side)^2 + (other shorter side)^2
You end up with the inequality that the unknown side must be less than < 8
Only I
Sarkar93
GMATinsight
Bunuel
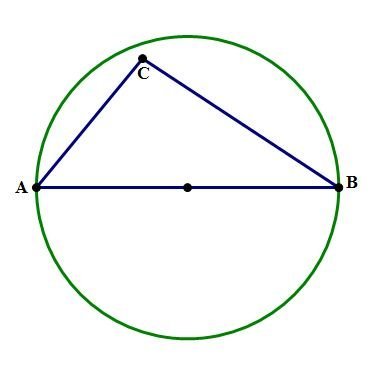
In the diagram above, AB = 10 is the diameter of the circle, and AC = 6. Given that point C is inside the circle, which could be the length of BC?
I. 7
II. 8
III. 9
A. I
B. II
C. III
D. I & II
E. II & III
Attachment:
triangle in circle.JPG
Here we can think of three properties
1) Sum of any two sides of the triangle > Third side
i.e. 16>BC >42) Angle drawn at circumference in a semicircle is a right angle
But here C is not on circumference i.e. ACB is an Obtuse angle triangle3) For any obtuse triangle \(c^2 > a^2 + b^2\) where c is the longest side of trianglei.e. \(b^2 < 10^2 - 6^2\)
i.e. \(b^2 < 100 - 36\)
i.e. \(b^2 < 64\)
i.e. \(b< 8\)
Answer: Option A
How did you know that this traiangle is an obtuse-angled triangle ?
Since the point C is not on the circumference of a triangle, this is not a right triangle I agree.
Now for any acute-angled triangle, \(a^2 + b^2 > c^2\) (where 'C' is the longest side)
Now, I can see from the three options given that all of them are less than 10. So '10' must be the longest side.
Hence, we need to see for which of the squares of 7/8/9 and 6 are less than the square of 10.
And that is for option A.
For option B, \(a^2 + b^2 = c^2\)
For option C, \(a^2 + b^2 < c^2\)
Kindly let me know what is wrong with my line of reasoning.

 55%
(hard)
55%
(hard)
 42%
(02:11)
wrong
42%
(02:11)
wrong  based on 218
sessions
based on 218
sessions