Events & Promotions
|
It is currently 19 Apr 2024, 15:07 |

Customized
for You
Track
Your Progress
Practice
Pays
11:00 AM IST
-01:00 PM IST
12:00 PM PDT
-01:00 PM PDT
08:30 AM PDT
-09:30 AM PDT
08:30 AM PDT
-09:30 AM PDT
10:00 AM PDT
-11:00 AM PDT
11:00 AM IST
-01:00 PM IST
12:00 PM EDT
-01:00 PM EDT
11:00 AM EDT
-12:00 PM EDT
06:45 AM PDT
-12:00 PM PDT
Difficulty:


 55%
(hard)
55%
(hard)
Question Stats:
64% (02:13) correct 36%
(02:04)
wrong
36%
(02:04)
wrong  based on 5610
sessions
based on 5610
sessions

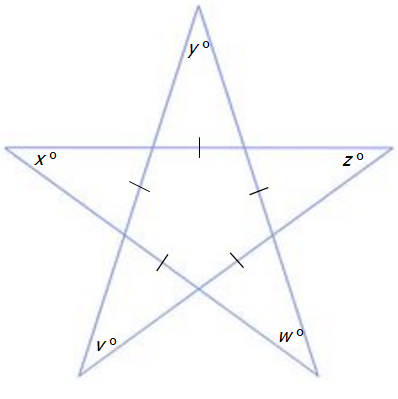
Star2.jpg [ 24.67 KiB | Viewed 140590 times ]


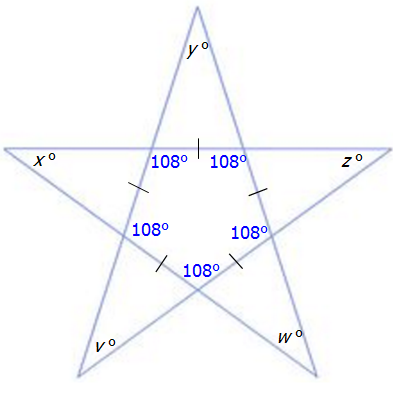
angles.jpg [ 12.75 KiB | Viewed 138166 times ]
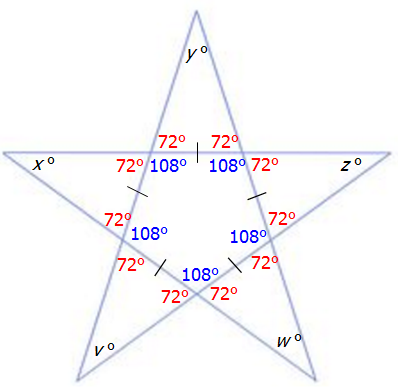
OG13-D10-A.png [ 26.98 KiB | Viewed 138411 times ]
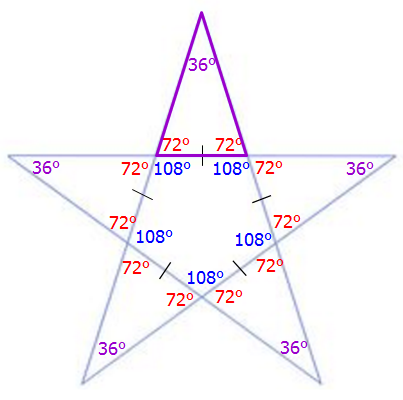
OG13-D10-B.png [ 38.38 KiB | Viewed 137936 times ]





File comment: y+A+B+C = 360 (sum of all the angles in quadrilateral-YABC )
A= 180-(y+v) (sum of all angles in a triangle is 180,Triangle YAV)
B= 180-(x+z) (Triangle XBZ)
C= 180-(y+w) (Triangle YCW)
Now, Substitute the values of A, B and C in the equation : A+B+C+y=360
(180-y-v) + (180-x-z) + (180-y-w) + y =360
By solving the above, we get:
540 - w - v - z - x - 2y + y=360
x+y+v+z+w=180
ANSWER - C
Govind Kohli
Kudos if this helps
step0004.png [ 5.55 KiB | Viewed 93244 times ]

GMAT.png [ 8.59 KiB | Viewed 93282 times ]


|
|
||
|
Hi Guest,
Here are updates for you:
ANNOUNCEMENTS
Tuck at Dartmouth
GMAT Club REWARDS
|