Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth
Kudos
Bookmarks
Tom and John both ride a bicycle in the same direction on an equal route at their constant speed rates of 20 km per hour and 12 km per hour, respectively. After 10 minutes Tom passes John, he reaches a gas station. How many minutes does it take John to reach the gas station?
A. 5 min
B. 6 min
C. 6 and \(\frac{2}{3}\) min
D. 10 min
E. 15 min
A. 5 min
B. 6 min
C. 6 and \(\frac{2}{3}\) min
D. 10 min
E. 15 min
Kudos
Bookmarks
Official Solution:
Tom and John both ride a bicycle in the same direction on an equal route at their constant speed rates of 20 km per hour and 12 km per hour, respectively. After 10 minutes Tom passes John, he reaches a gas station. How many minutes does it take John to reach the gas station?
A. 5 min
B. 6 min
C. 6 and \(\frac{2}{3}\) min
D. 10 min
E. 15 min
In general, for velocity question, the fact that the same time passes applies.
John: \(12km:1hr=12km:60min=2km:10min\)
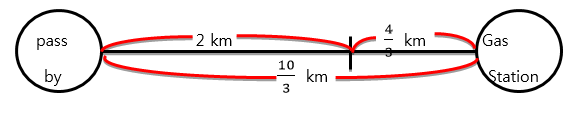
Tom: \(20km:1hr = 20km:60min = \frac{20}{6}km:10min = \frac{10}{3}km:10min\)
As shown in the diagram above, Tom passes by John, and gets to the gas station after 10 minutes. This means that Tom went \(\frac{10}{3}\) km, and John went 2 km since the same time has passed. (\(\frac{10}{3}-2)\)km = \(\frac{4}{3}\)km, then for John \(2km:10min\), then \(1km:5min\), and if you multiply both sides by \(\frac{4}{3}\), then
\(\frac{4}{3}km: (\frac{4}{3})5min,\) so \((\frac{4}{3})5min = \frac{20}{3}min = 6\) and \(\frac{2}{3} min\). The answer is C.
Answer: C
Tom and John both ride a bicycle in the same direction on an equal route at their constant speed rates of 20 km per hour and 12 km per hour, respectively. After 10 minutes Tom passes John, he reaches a gas station. How many minutes does it take John to reach the gas station?
A. 5 min
B. 6 min
C. 6 and \(\frac{2}{3}\) min
D. 10 min
E. 15 min
In general, for velocity question, the fact that the same time passes applies.
John: \(12km:1hr=12km:60min=2km:10min\)

Tom: \(20km:1hr = 20km:60min = \frac{20}{6}km:10min = \frac{10}{3}km:10min\)
As shown in the diagram above, Tom passes by John, and gets to the gas station after 10 minutes. This means that Tom went \(\frac{10}{3}\) km, and John went 2 km since the same time has passed. (\(\frac{10}{3}-2)\)km = \(\frac{4}{3}\)km, then for John \(2km:10min\), then \(1km:5min\), and if you multiply both sides by \(\frac{4}{3}\), then
\(\frac{4}{3}km: (\frac{4}{3})5min,\) so \((\frac{4}{3})5min = \frac{20}{3}min = 6\) and \(\frac{2}{3} min\). The answer is C.
Answer: C
Moderator:





