Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 09 Dec 2016, 10:39.
Last edited by EgmatQuantExpert on 18 Oct 2018, 02:06, edited 18 times in total.
Last edited by EgmatQuantExpert on 18 Oct 2018, 02:06, edited 18 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
This is the third and final article in our series of articles on Triangles. In case you haven’t gone through the previous articles, we strongly suggest that you go through them before reading this article. The previous articles can be accessed using the following links:
In the above articles, we have discussed the following aspects:
Carrying on with the discussion, let’s now look at the last article on Triangles, where 3 special properties will be discussed which are tested by GMAT.
We will also apply the learning from this article on three GMAT like questions to understand the application of the concepts.
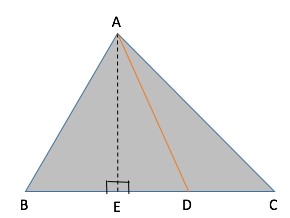
Consider any triangle ABC and draw a line joining A to the midpoint of BC. Let’s call this line AD.
Now tell me, what can we infer about the area of triangle ABD and ACD? Is there any relation between them?
We know, Area of a triangle = (\(1/2\)) \(* base * height\)
So, let us drop a perpendicular from A on BC and name it AE. Since the heights of triangle ABD and ACD are equal to AE, we can write:
• Area of triangle \(ABD\) = \(½ * BD * AE\) and Area of triangle \(ACD\) = \(½ * CD * AE\)
Also, since D is the midpoint of BC, we have \(CD = BD\). Hence, we can conclude that:
Area of triangle ABD = Area of triangle ACD.
We know that the line joining a vertex of a triangle to the midpoint of the opposite side is called a median of the triangle.
Let us look at an Official question which can be solved very quickly, using the above property.

Property of a Median playing an important role in a OG Question. A slightly edited version of OG Question: OG 16 DS 126
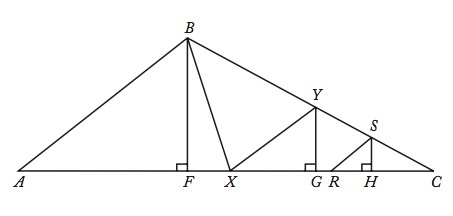
In triangle ABC, point X is the midpoint of side AC and point Y is the midpoint of side BC. If point R is the midpoint of line segment XC and if point S is the midpoint of line segment YC, what is the area of triangular region RCS, if the area of triangular region ABX is 32 square units?
This diagram might look scary and the question might seem undoable at the beginning. But let us simplify the diagram, concentrating only on the medians, BX, XY, RS and RY (join RY in the diagram). On doing so, the diagram will look as follows:
Solution:
Since BX is a median in triangle ABC, we can use the Special Property to conclude that, Area of ABX = Area of BXC
It is given that the area of triangle ABX = 32 square units. Hence, Area of BXC = 32 square units.
Since XY is a median in triangle BXC, we can conclude that
• Area of BXY = Area of XYC = \(32/2\) = 16
Since RY is a median in triangle XYC, we can conclude that
• Area of RYX = Area of RYC = \(16/2\)= 8
And since RS is a median in triangle YRC we can conclude that
• Area of YRS = Area of RCS =\(8/2\) = 4
So, is this question really tough? Definitely, not as tough as it looked at the beginning. We used one simple and special property to elegantly solve a complicated looking question.
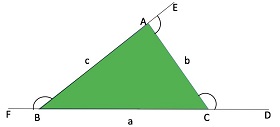
We know that, an external angle = sum of two opposite interior angles. In the above diagram, ABC is a triangle with sides extended as shown. Therefore, using the above property we can write,
Ext. Angle ACD = int. angle CAB + int. angle CBA
But hold on, that is not the special property! Now you know that the sum of internal angles = \(180^0\).
But what about the sum of external angles? If we add up all the external angles as shown in the diagram, we will get
We will discuss this property in more details for Polygons, where I will show you that sum of external angles is equal to \(360^0\) for any convex polygon, irrespective of the number of sides the polygon has.
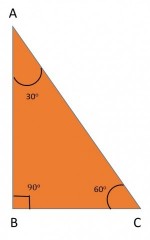
While going through GMAT questions on right angled triangles, the most commonly tested right angled triangles are ones with the following set of values as its angles.
1. \(30^0\) -\(60^0\)- \(90^0\) or 2. \(45^0\)-\(45^0\)-\(90^0\).
Therefore, it is important for us to know the relation between these angles and the sides of the triangles, as knowing this can help us in finding the answer quickly and at the same make the calculations significantly simple.
As shown in the figure, if the angles of the triangle are \(30^0\)- \(60^0\)- \(90^0\), the ratio of the sides will be –
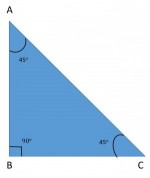
1. As shown in the figure, if the angles of the triangle are \(45^0\)- \(45^0\)- \(90^0\), the ratio of the sides will be –
Note: The above ratio can easily be proved using Trigonometry values.

Let us apply the special property 2 and 3 in a very simple GMAT like question. The two questions given below are based on the same diagram, so lets solve these questions together to understand the application of the above properties.
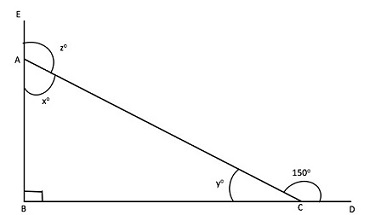
Q.1 What is the value of z?
Q.2 If the value of \(AC = 4 units\), what is the ratio of the sides \(AB\) and \(BC\)?
Solution to Q1:
Notice carefully, that z is the external angle of triangle ABC. From our conceptual understanding related to angles of a triangle, we can write –
From the diagram, we can clearly infer that –
Also,
Hence, the value of Angle z = Angle \(ABC\) + Angle \(ACB\) = \(90^0\) + \(30^0\) = \(120^0\).
Solution to Q2:
This question can be solved in multiple ways –
1. Method - I:
We know that \(AC = 4 units\), and from our above discussion in part 1 we know that angle \(ACB\) = \(30^0\). [/list]
Therefore,
Therefore, ratio of \(AB : BC\) =\(2 : 2√3 = 1 : √3\)
2. Method - II:
But say one does not know trigonometry but still wants to solve it. This is where, our Special Property 3, Case 1 comes in handy!
Therefore, from here, we can directly say that the answer would be 1 : √3 and we don’t even have to use the value of AC to find the answer!
Cool isn’t it?
Now, let us come to the last example of our article, where we will try to apply the third property in a question, which not only focuses our conceptual knowledge but also tests are ability to represent the information in a diagrammatically correct manner.

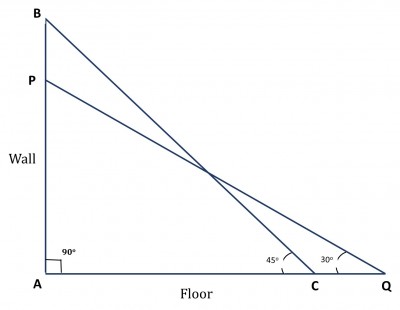
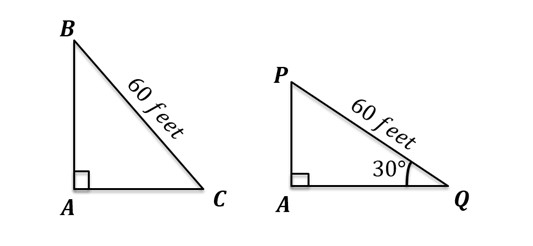
A 60 feet long ladder is inclined against a wall such that the bottom and the top of the ladder are at equal distance from the point where the wall meets the floor. The same ladder slides away from the foot of the wall such that it is inclined at an angle of \(30^0\) from the floor. What is the difference between the heights to which the ladder reaches in the two cases?
Solution:
Now this question might seem to be a tough one, because the position of the ladder is different in the two cases, which leads to change in the angles with respect to the floor. Therefore, most students might feel that this question might not be an easy one to solve.
But no need to worry, let’s see how by using our special property and a methodical approach, we can get our answer very easily!
Step 1: Drawing Inferences from the Question Statement
Let us represent the two cases diagrammatically.
Triangle BAC represents the initial case, where point A is the point of intersection of the wall and the floor and BC represents the ladder. We are given that AB = AC and BC = 60 feet.
Triangle PAQ represents the case after the ladder slided. The only value that remains unchanged is the length of the ladder, hence BC = PQ.
Therefore, in the Right Triangle PAQ, \(PQ = 60 feet\), and Angle \(AQP = 30^°\)
We need to find the value of AB – AP.
Step 2: Finding required values
Let us first consider Right Triangle BAC:
We know that when two sides of a right triangle are equal, it is \(45^0\)-\(45^0\)-\(90^0\) triangle.
As discussed in special property 3, in such a triangle, the sides opposite to the angles \(45^0\),\(45^0\), and \(90^0\) respectively are in the ratio 1: 1: √2
Therefore,
\(AB/BC=1/(√2)\)
Or, \(AB=BC/√2=60/√2=30√2\)
Thus, we have found out the value of AB.
Now, considering Right Triangle PAQ:
It is \(30^0\) –\(60^0\)-\(90^0\) right angled triangle.
And we know that in such a triangle, the sides opposite to the angles \(30^0\), \(60^0\), and \(90^0\) respectively are in the ratio 1 : √3 : 2.
Therefore, \(AP/PQ=1/2\)
Or, \(AP=PQ/2=60/2=30\)
Step 3: Calculate the final answer
Difference between the heights to which the ladder reaches in the two cases\(= AB – AP = 30√2 - 30 = 30(√2 – 1)\)
Answer: Option (B)

Any geometry question testing the concepts of triangles can be easily tackled as long as the test taker is clear with:
Practice questions will be posted in a few days to test your understanding of all the concepts that we have discussed in our three articles. Feel free to post any question till then.
Link to the previous articles in this series
Mastering Important Concept Tested by GMAT on Triangles – III
This is the third and final article in our series of articles on Triangles. In case you haven’t gone through the previous articles, we strongly suggest that you go through them before reading this article. The previous articles can be accessed using the following links:
- Mastering Important Concepts Tested by GMAT in Triangles – I
Mastering Important Concepts Tested by GMAT in Triangles – II
In the above articles, we have discussed the following aspects:
- 1. Identifying whether a set of given numbers could be the lengths of the three sides of a triangle.
2. Range of possible values of the length of one side of a triangle given the lengths of the other two sides.
3. Key properties related to the angles of a triangle.
4. Key properties of different types of triangles tested on the GMAT.
Carrying on with the discussion, let’s now look at the last article on Triangles, where 3 special properties will be discussed which are tested by GMAT.
We will also apply the learning from this article on three GMAT like questions to understand the application of the concepts.
1. LEARN HOW A MEDIAN AFFECTS THE AREA OF ANY TRIANGLE
Consider any triangle ABC and draw a line joining A to the midpoint of BC. Let’s call this line AD.
Now tell me, what can we infer about the area of triangle ABD and ACD? Is there any relation between them?
We know, Area of a triangle = (\(1/2\)) \(* base * height\)
So, let us drop a perpendicular from A on BC and name it AE. Since the heights of triangle ABD and ACD are equal to AE, we can write:
• Area of triangle \(ABD\) = \(½ * BD * AE\) and Area of triangle \(ACD\) = \(½ * CD * AE\)
Also, since D is the midpoint of BC, we have \(CD = BD\). Hence, we can conclude that:
Area of triangle ABD = Area of triangle ACD.
We know that the line joining a vertex of a triangle to the midpoint of the opposite side is called a median of the triangle.
Therefore, we found that the median AD divides the triangle into two equal areas.
Let us look at an Official question which can be solved very quickly, using the above property.

Property of a Median playing an important role in a OG Question. A slightly edited version of OG Question: OG 16 DS 126
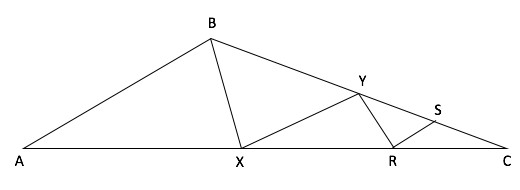
In triangle ABC, point X is the midpoint of side AC and point Y is the midpoint of side BC. If point R is the midpoint of line segment XC and if point S is the midpoint of line segment YC, what is the area of triangular region RCS, if the area of triangular region ABX is 32 square units?
This diagram might look scary and the question might seem undoable at the beginning. But let us simplify the diagram, concentrating only on the medians, BX, XY, RS and RY (join RY in the diagram). On doing so, the diagram will look as follows:
Solution:
Since BX is a median in triangle ABC, we can use the Special Property to conclude that, Area of ABX = Area of BXC
It is given that the area of triangle ABX = 32 square units. Hence, Area of BXC = 32 square units.
Since XY is a median in triangle BXC, we can conclude that
• Area of BXY = Area of XYC = \(32/2\) = 16
Since RY is a median in triangle XYC, we can conclude that
• Area of RYX = Area of RYC = \(16/2\)= 8
And since RS is a median in triangle YRC we can conclude that
• Area of YRS = Area of RCS =\(8/2\) = 4
So, is this question really tough? Definitely, not as tough as it looked at the beginning. We used one simple and special property to elegantly solve a complicated looking question.
2. DISCOVER THE PROPERTY OF SUM OF EXTERNAL ANGLES OF A TRIANGLE
We know that, an external angle = sum of two opposite interior angles. In the above diagram, ABC is a triangle with sides extended as shown. Therefore, using the above property we can write,
Ext. Angle ACD = int. angle CAB + int. angle CBA
But hold on, that is not the special property! Now you know that the sum of internal angles = \(180^0\).
But what about the sum of external angles? If we add up all the external angles as shown in the diagram, we will get
\(Ext Angles (ACD + CAE + ABF)\) = \(int. angles (2A + 2B + 2C)\) = \(2 * 180^0\) = \(360^0\)
Hence, the sum of external angles = \(360^0\).
We will discuss this property in more details for Polygons, where I will show you that sum of external angles is equal to \(360^0\) for any convex polygon, irrespective of the number of sides the polygon has.
3. CHEEKY TRICK ON ANGLE-SIDE PROPERTY OF SPECIAL RIGHT ANGLED TRIANGLES
While going through GMAT questions on right angled triangles, the most commonly tested right angled triangles are ones with the following set of values as its angles.
1. \(30^0\) -\(60^0\)- \(90^0\) or 2. \(45^0\)-\(45^0\)-\(90^0\).
Therefore, it is important for us to know the relation between these angles and the sides of the triangles, as knowing this can help us in finding the answer quickly and at the same make the calculations significantly simple.
Case 1:
As shown in the figure, if the angles of the triangle are \(30^0\)- \(60^0\)- \(90^0\), the ratio of the sides will be –
\(AB: BC: AC = 1: √3: 2\)
Case 2:
1. As shown in the figure, if the angles of the triangle are \(45^0\)- \(45^0\)- \(90^0\), the ratio of the sides will be –
\(AB: BC: AC = 1: 1: √2\)
Note: The above ratio can easily be proved using Trigonometry values.

Application of Special Properties on a question similar to OG16 -PS214
Let us apply the special property 2 and 3 in a very simple GMAT like question. The two questions given below are based on the same diagram, so lets solve these questions together to understand the application of the above properties.
Q.1 What is the value of z?
- a. \(110^0\)
b. \(120^0\)
c. \(130^0\)
d. \(140^0\)
e. \(150^0\)
Q.2 If the value of \(AC = 4 units\), what is the ratio of the sides \(AB\) and \(BC\)?
- a. 2 : 1
b. 1 : √3
c. 2 : √3
d. √3 : 1
e. 1 : 2
Solution to Q1:
Notice carefully, that z is the external angle of triangle ABC. From our conceptual understanding related to angles of a triangle, we can write –
- • External Angle \(CAE\) = sum of opposite internal angles of triangle \(ABC\)
• Therefore, Angle z = Angle \(ABC\) + Angle \(ACB\)
From the diagram, we can clearly infer that –
- • Angle \(ABC\) = \(90^0\) and Angle\(ACB\) = \(y^0\).
Also,
- • Angle \(ACB\) + Angle \(ACD\) = \(180^0\), [straight line angle property]
- • Angle \(ACD\) = \(150^0\)
- o Therefore, Angle \(ACB\) = \(180^0\) – \(150^0\) = \(30^0\).
Hence, the value of Angle z = Angle \(ABC\) + Angle \(ACB\) = \(90^0\) + \(30^0\) = \(120^0\).
Solution to Q2:
This question can be solved in multiple ways –
1. Method - I:
We know that \(AC = 4 units\), and from our above discussion in part 1 we know that angle \(ACB\) = \(30^0\). [/list]
Therefore,
- o length \(AB\) = \(AC\) \(sin\) \(30^0\) = \(4 * ½ = 2\)
o And \(BC = AC\) \(cos\) \(30^0\) = \(4 * √3/2 = 2√3\)
Therefore, ratio of \(AB : BC\) =\(2 : 2√3 = 1 : √3\)
2. Method - II:
But say one does not know trigonometry but still wants to solve it. This is where, our Special Property 3, Case 1 comes in handy!
- o If we observe carefully, we will notice that triangle ABC is a \(30^0\) –\(60^0\) –\(90^0\) triangle.
o Since \(ABC = 90^0\) , \(BAC = 60^0\) and \(ACB = 30^0\)
o And we know that ratio of AB : BC : CA = 1 : √3 : 2
Therefore, from here, we can directly say that the answer would be 1 : √3 and we don’t even have to use the value of AC to find the answer!
Cool isn’t it?
Now, let us come to the last example of our article, where we will try to apply the third property in a question, which not only focuses our conceptual knowledge but also tests are ability to represent the information in a diagrammatically correct manner.

A question to test your imagination!!
A 60 feet long ladder is inclined against a wall such that the bottom and the top of the ladder are at equal distance from the point where the wall meets the floor. The same ladder slides away from the foot of the wall such that it is inclined at an angle of \(30^0\) from the floor. What is the difference between the heights to which the ladder reaches in the two cases?
- A. 15(√2 – 1)
B. 30(√2 – 1)
C. 15(√2 + 1)
D. 30√2
E. 30(√2 + 1)
Solution:
Now this question might seem to be a tough one, because the position of the ladder is different in the two cases, which leads to change in the angles with respect to the floor. Therefore, most students might feel that this question might not be an easy one to solve.
But no need to worry, let’s see how by using our special property and a methodical approach, we can get our answer very easily!
Step 1: Drawing Inferences from the Question Statement
Let us represent the two cases diagrammatically.
Triangle BAC represents the initial case, where point A is the point of intersection of the wall and the floor and BC represents the ladder. We are given that AB = AC and BC = 60 feet.
Triangle PAQ represents the case after the ladder slided. The only value that remains unchanged is the length of the ladder, hence BC = PQ.
Therefore, in the Right Triangle PAQ, \(PQ = 60 feet\), and Angle \(AQP = 30^°\)
We need to find the value of AB – AP.
Step 2: Finding required values
Let us first consider Right Triangle BAC:
We know that when two sides of a right triangle are equal, it is \(45^0\)-\(45^0\)-\(90^0\) triangle.
As discussed in special property 3, in such a triangle, the sides opposite to the angles \(45^0\),\(45^0\), and \(90^0\) respectively are in the ratio 1: 1: √2
Therefore,
\(AB/BC=1/(√2)\)
Or, \(AB=BC/√2=60/√2=30√2\)
Thus, we have found out the value of AB.
Now, considering Right Triangle PAQ:
It is \(30^0\) –\(60^0\)-\(90^0\) right angled triangle.
And we know that in such a triangle, the sides opposite to the angles \(30^0\), \(60^0\), and \(90^0\) respectively are in the ratio 1 : √3 : 2.
Therefore, \(AP/PQ=1/2\)
Or, \(AP=PQ/2=60/2=30\)
Step 3: Calculate the final answer
Difference between the heights to which the ladder reaches in the two cases\(= AB – AP = 30√2 - 30 = 30(√2 – 1)\)
Answer: Option (B)

What did we learn???
Any geometry question testing the concepts of triangles can be easily tackled as long as the test taker is clear with:
- a. the basic properties of a triangle
b. the subtle differences these properties exhibit, depending on the type of the triangle
c. when to apply and how to apply these basic properties.
Practice questions will be posted in a few days to test your understanding of all the concepts that we have discussed in our three articles. Feel free to post any question till then.
Link to the previous articles in this series
- Mastering Important Concepts Tested by GMAT in Triangles – I
Mastering Important Concepts Tested by GMAT in Triangles – II
Attachments
![]() Triangle_3_V1.pdf [1.47 MiB]
Triangle_3_V1.pdf [1.47 MiB]
Downloaded 685 times
Originally posted by EgmatQuantExpert on 09 Dec 2016, 11:31.
Last edited by EgmatQuantExpert on 07 Aug 2018, 09:03, edited 1 time in total.
Last edited by EgmatQuantExpert on 07 Aug 2018, 09:03, edited 1 time in total.
Kudos
Bookmarks
Hey Everyone,
Links of two practice questions are given below, specifically designed to help you apply the learnings from this article.
Exercise Questions
Question 1
Question 2
Detailed solutions will be posted soon.
Happy Learning!
Thanks,
Saquib
Quant Expert
e-GMAT
Links of two practice questions are given below, specifically designed to help you apply the learnings from this article.
Exercise Questions
Question 1
Question 2
Detailed solutions will be posted soon.
Happy Learning!
Thanks,
Saquib
Quant Expert
e-GMAT
Kudos
Bookmarks
Hey Everyone,
The question links have been posted.
Please Note : The official solution will be posted on 15th of December. Expecting active participation from everyone
Thanks,
Saquib
Quant Expert
e-GMAT
The question links have been posted.
Please Note : The official solution will be posted on 15th of December. Expecting active participation from everyone
Thanks,
Saquib
Quant Expert
e-GMAT