Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
COORDINATE GEOMETRY
This post is a part of [GMAT MATH BOOK]
created by: Bunuel
edited by: bb, walker
Definition
Coordinate geometry, or Cartesian geometry, is the study of geometry using a coordinate system and the principles of algebra and analysis.
The Coordinate Plane
In coordinate geometry, points are placed on the "coordinate plane" as shown below. The coordinate plane is a two-dimensional surface on which we can plot points, lines and curves. It has two scales, called the x-axis and y-axis, at right angles to each other. The plural of axis is 'axes' (pronounced "AXE-ease").
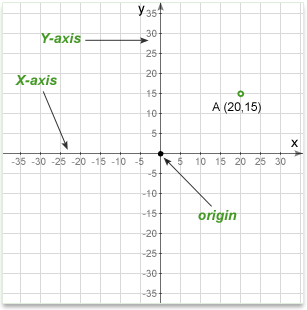
A point's location on the plane is given by two numbers, one that tells where it is on the x-axis and another which tells where it is on the y-axis. Together, they define a single, unique position on the plane. So in the diagram above, the point A has an x value of 20 and a y value of 15. These are the coordinates of the point A, sometimes referred to as its "rectangular coordinates".
X axis
The horizontal scale is called the x-axis and is usually drawn with the zero point in the middle. Values to the right are positive and those to the left are negative.
Y axis
The vertical scale is called the y-axis and is also usually drawn with the zero point in the middle. Values above the origin are positive and those below are negative.
Origin
The point where the two axes cross (at zero on both scales) is called the origin.
Quadrants
When the origin is in the center of the plane, they divide it into four areas called quadrants.
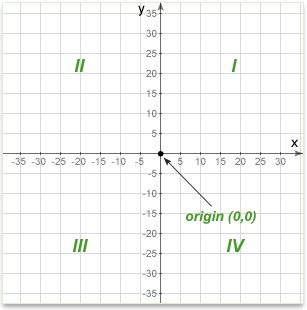
The first quadrant, by convention, is the top right, and then they go around counter-clockwise. In the diagram above they are labeled Quadrant 1, 2 etc. It is conventional to label them with numerals but we talk about them as "first, second, third, and fourth quadrant".
Point (x,y)
The coordinates are written as an "ordered pair". The letter P is simply the name of the point and is used to distinguish it from others.
The two numbers in parentheses are the x and y coordinate of the point. The first number (x) specifies how far along the x (horizontal) axis the point is. The second is the y coordinate and specifies how far up or down the y axis to go. It is called an ordered pair because the order of the two numbers matters - the first is always the x (horizontal) coordinate.
The sign of the coordinate is important. A positive number means to go to the right (x) or up (y). Negative numbers mean to go left (x) or down (y).
Distance between two points
Given coordinates of two points, distance D between two points is given by:
\(D=\sqrt{dx^2+dy^2}\) (where \(dx\) is the difference between the x-coordinates and \(dy\) is the difference between the y-coordinates of the points)
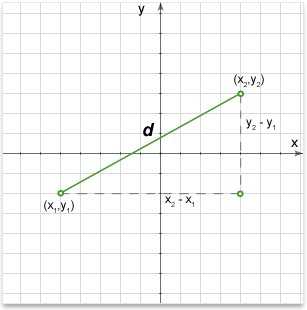
As you can see, the distance formula on the plane is derived from the Pythagorean theorem.
Above formula can be written in the following way for given two points \((x_1,y_1)\) and \((x_2,y_2)\):
\(D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Vertical and horizontal lines
If the line segment is exactly vertical or horizontal, the formula above will still work fine, but there is an easier way. For a horizontal line, its length is the difference between the x-coordinates. For a vertical line its length is the difference between the y-coordinates.
Distance between the point A (x,y) and the origin
As the one point is origin with coordinate O (0,0) the formula can be simplified to:
\(D=\sqrt{x^2+y^2}\)
Example #1
Q: Find the distance between the point A (3,-1) and B (-1,2)
Solution: Substituting values in the equation we'll get
\(D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
\(D=\sqrt{(-1-3)^2+(2-(-1))^2}=\sqrt{16+9}=5\)
Midpoint of a Line Segment
A line segment on the coordinate plane is defined by two endpoints whose coordinates are known. The midpoint of this line is exactly halfway between these endpoints and it's location can be found using the Midpoint Theorem, which states:
• The x-coordinate of the midpoint is the average of the x-coordinates of the two endpoints.
• Likewise, the y-coordinate is the average of the y-coordinates of the endpoints.

Coordinates of the midpoint \(M (x_m,y_m)\) of the line segment AB, (\(A (x_1,y_1)\) and \(B (x_2,y_2)\)) are \(x_m=\frac{x_1+x_2}{2}\) and \(y_m=\frac{y_1+y_2}{2}\)
Lines in Coordinate Geometry
In Euclidean geometry, a line is a straight curve. In coordinate geometry, lines in a Cartesian plane can be described algebraically by linear equations and linear functions.
Every straight line in the plane can represented by a first degree equation with two variables.
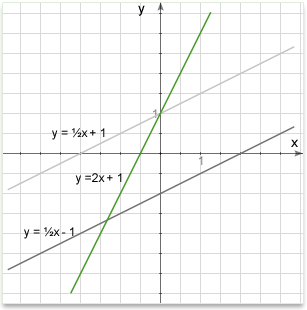
There are several approaches commonly used in coordinate geometry. It does not matter whether we are talking about a line, ray or line segment. In all cases any of the below methods will provide enough information to define the line exactly.
1. General form.
The general form of the equation of a straight line is
\(ax+by+c=0\)
Where \(a\), \(b\) and \(c\) are arbitrary constants. This form includes all other forms as special cases. For an equation in this form the slope is \(-\frac{a}{b}\) and the y intercept is \(-\frac{c}{b}\).
2. Point-intercept form.
\(y=mx+b\)
Where: \(m\) is the slope of the line; \(b\) is the y-intercept of the line; \(x\) is the independent variable of the function \(y\).
3. Using two points
In figure below, a line is defined by the two points A and B. By providing the coordinates of the two points, we can draw a line. No other line could pass through both these points and so the line they define is unique.
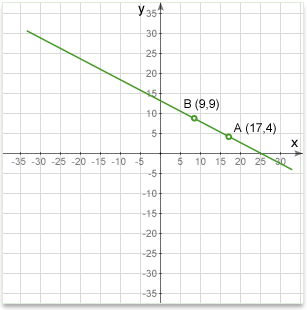
The equation of a straight line passing through points \(P_1(x_1, y_1)\) and \(P_2(x_2, y_2)\) is:
\(\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}\)
Example #1
Q: Find the equation of a line passing through the points A (17,4) and B (9,9).
Solution: Substituting the values in equation \(\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}\) we'll get: \(\frac{y-4}{x-17}=\frac{4-9}{17-9}\)
\(\frac{y-4}{x-17}=\frac{-5}{8}\) --> \(8y-32=-5x+85\) --> \(8y+5x-117=0\) OR if we want to write the equation in the slope-intercept form: \(y=-\frac{5}{8}x+\frac{117}{8}\)
4. Using one point and the slope
Sometimes on the GMAT you will be given a point on the line and its slope and from this information you will need to find the equation or check if this line goes through another point. You can think of the slope as the direction of the line. So once you know that a line goes through a certain point, and which direction it is pointing, you have defined one unique line.
In figure below, we see a line passing through the point A at (14,23). We also see that it's slope is +2 (which means it goes 2 up for every one across). With these two facts we can establish a unique line.
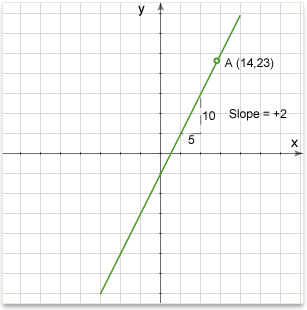
The equation of a straight line that passes through a point \(P_1(x_1, y_1)\) with a
slope m is:
\(y-y_1=m(x-x_1)\)
Example #2
Q: Find the equation of a line passing through the point A (14,23) and the slope 2.
Solution: Substituting the values in equation \(y-y_1=m(x-x_1)\) we'll get \(y-23=2(x-14)\) --> \(y=2x-5\)
4. Intercept form.
The equation of a straight line whose x and y intercepts are a and b, respectively, is:
\(\frac{x}{a}+\frac{y}{b}=1\)
Example #3
Q: Find the equation of a line whose x intercept is 5 and y intercept is 2.
Solution: Substituting the values in equation \(\frac{x}{a}+\frac{y}{b}=1\) we'll get \(\frac{x}{5}+\frac{y}{2}=1\) --> \(5y+2x-10=0\) OR if we want to write the equation in the slope-intercept form: \(y=-\frac{2}{5}x+2\)
Slope of a Line
The slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline.
The slope is defined as the ratio of the "rise" divided by the "run" between two points on a line, or in other words, the ratio of the altitude change to the horizontal distance between any two points on the line.

Given two points \((x_1,y_1)\) and \((x_2,y_2)\) on a line, the slope \(m\) of the line is:
\(m=\frac{y_2-y_1}{x_2-x_1}\)
If the equation of the line is given in the Point-intercept form: \(y=mx+b\), then \(m\) is the slope. This form of a line's equation is called the slope-intercept form, because \(b\) can be interpreted as the y-intercept of the line, the y-coordinate where the line intersects the y-axis.
If the equation of the line is given in the General form:\(ax+by+c=0\), then the slope is \(-\frac{a}{b}\) and the y intercept is \(-\frac{c}{b}\).
SLOPE DIRECTION
The slope of a line can be positive, negative, zero or undefined.
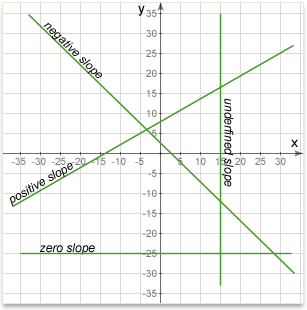
Positive slope
Here, y increases as x increases, so the line slopes upwards to the right. The slope will be a positive number. The line below has a slope of about +0.3, it goes up about 0.3 for every step of 1 along the x-axis.
Negative slope
Here, y decreases as x increases, so the line slopes downwards to the right. The slope will be a negative number. The line below has a slope of about -0.3, it goes down about 0.3 for every step of 1 along the x-axis.
Zero slope
Here, y does not change as x increases, so the line in exactly horizontal. The slope of any horizontal line is always zero. The line below goes neither up nor down as x increases, so its slope is zero.
Undefined slope
When the line is exactly vertical, it does not have a defined slope. The two x coordinates are the same, so the difference is zero. The slope calculation is then something like \(slope=\frac{15}{0}\) When you divide anything by zero the result has no meaning. The line above is exactly vertical, so it has no defined slope.
SLOPE AND QUADRANTS:
1. If the slope of a line is negative, the line WILL intersect quadrants II and IV. X and Y intercepts of the line with negative slope have the same sign. Therefore if X and Y intersects are positive, the line intersects quadrant I; if negative, quadrant III.
2. If the slope of line is positive, line WILL intersect quadrants I and III. Y and X intercepts of the line with positive slope have opposite signs. Therefore if X intersect is negative, line intersects the quadrant II too, if positive quadrant IV.
3. Every line (but the one crosses origin OR parallel to X or Y axis OR X and Y axis themselves) crosses three quadrants. Only the line which crosses origin \((0,0)\) OR is parallel to either of axis crosses only two quadrants.
4. If a line is horizontal it has a slope of \(0\), is parallel to X-axis and crosses quadrant I and II if the Y intersect is positive OR quadrants III and IV, if the Y intersect is negative. Equation of such line is y=b, where b is y intersect.
5. If a line is vertical, the slope is not defined, line is parallel to Y-axis and crosses quadrant I and IV, if the X intersect is positive and quadrant II and III, if the X intersect is negative. Equation of such line is \(x=a\), where a is x-intercept.
6. For a line that crosses two points \((x_1,y_1)\) and \((x_2,y_2)\), slope \(m=\frac{y_2-y_1}{x_2-x_1}\)
7. If the slope is 1 the angle formed by the line is \(45\) degrees.
8. Given a point and slope, equation of a line can be found. The equation of a straight line that passes through a point \((x_1, y_1)\) with a slope \(m\) is: \(y - y_1 = m(x - x_1)\)
Vertical and horizontal lines
A vertical line is parallel to the y-axis of the coordinate plane. All points on the line will have the same x-coordinate.
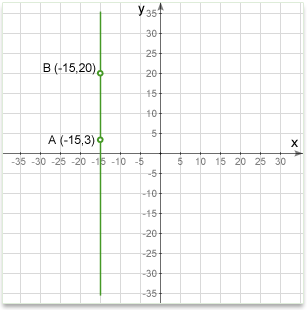
A vertical line has no slope. Or put another way, for a vertical line the slope is undefined.
The equation of a vertical line is:
\(x=a\)
Where: x is the coordinate of any point on the line; a is where the line crosses the x-axis (x intercept). Notice that the equation is independent of y. Any point on the vertical line satisfies the equation.
A horizontal line is parallel to the x-axis of the coordinate plane. All points on the line will have the same y-coordinate.

A horizontal line has a slope of zero.
The equation of a horizontal line is:
\(y=b\)
Where: y is the coordinate of any point on the line; b is where the line crosses the y-axis (y intercept). Notice that the equation is independent of x. Any point on the horizontal line satisfies the equation.
Parallel lines
Parallel lines have the same slope.
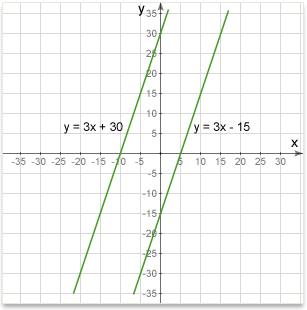
The slope can be found using any method that is convenient to you:
From two given points on the line.
From the equation of the line in slope-intercept form
From the equation of the line in point-slope form
The equation of a line through the point \(P_1(x_1, y_1)\) and parallel to line \(ax + by + c = 0\) is:
\(a(x - x_1) + b(y - y_1) = 0\)
Distance between two parallel lines \(y=mx+b\) and \(y=mx+c\) can be found by the formula:
\(D=\frac{|b-c|}{\sqrt{m^2+1}}\)
Example #1
Q:There are two lines. One line is defined by two points at (5,5) and (25,15). The other is defined by an equation in slope-intercept form form y = 0.52x - 2.5. Are two lines parallel?
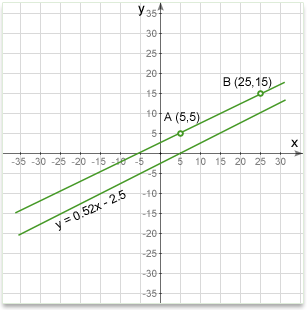
Solution:
For the top line, the slope is found using the coordinates of the two points that define the line. \(Slope=\frac{15-5}{25-5}=0.5\)
For the lower line, the slope is taken directly from the formula. Recall that the slope intercept formula is y = mx + b, where m is the slope. So looking at the formula we see that the slope is 0.52.
So, the top one has a slope of 0.5, the lower slope is 0.52, which are not equal. Therefore, the lines are not parallel.
Example #2
Q: Define a line through a point C parallel to a line passes through the points A and B.

Solution: We first find the slope of the line AB using the same method as in the example above.
\(Slope AB=\frac{20-7}{5-30}=-0.52\)
For the line to be parallel to AB it will have the same slope, and will pass through a given point, C(12,10). We therefore have enough information to define the line by it's equation in point-slope form form:
\(y=-0.52(x-12)+10\) --> \(y=-0.52x+16.24\)
Perpendicular lines
For one line to be perpendicular to another, the relationship between their slopes has to be negative reciprocal \(-\frac{1}{m}\). In other words, the two lines are perpendicular if and only if the product of their slopes is \(-1\).
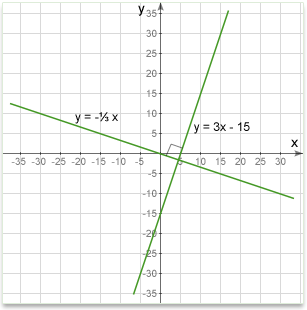
The two lines \(a_1x + b_1y + c_1 = 0\) and \(a_2x + b_2y + c_2 = 0\) are perpendicular if \(a_1a_2 + b_1b_2 = 0\).
The equation of a line passing through the point \(P_1(x_1, y_1\)) and perpendicular to line \(ax + by + c = 0\) is:
\(b(x - x_1)-a(y - y_1) = 0\)
Example #1:
Q: Are the two lines below perpendicular?
Solution:
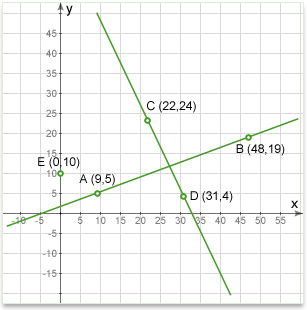
To answer, we must find the slope of each line and then check to see if one slope is the negative reciprocal of the other or if their product equals to -1.
\(Slope AB=\frac{5-19}{9-48}=\frac{-14}{-39}=0.358\)
\(Slope CD=\frac{24-4}{22-31}=\frac{20}{-9}=-2.22\)
If the lines are perpendicular, each will be the negative reciprocal of the other. It doesn't matter which line we start with, so we will pick AB:
Negative reciprocal of 0.358 is \(-\frac{1}{0.358}=-2.79\)
So, the slope of CD is -2.22, and the negative reciprocal of the slope of AB is -2.79. These are not the same, so the lines are not perpendicular, even though they may look as though they are. However, if you looked carefully at the diagram, you might have noticed that point C is a little too far to the left for the lines to be perpendicular.
Example # 2.
Q: Define a line passing through the point E and perpendicular to a line passing through the points C and D on the graph above.
Solution: The point E is on the y-axis and so is the y-intercept of the desired line. Once we know the slope of the line, we can express it using its equation in slope-intercept form y=mx+b, where m is the slope and b is the y-intercept.
First find the slope of line CD:
\(Slope CD=\frac{24-4}{22-31}=\frac{20}{-9}=-2.22\)
The line we seek will have a slope which is the negative reciprocal of:
\(-\frac{1}{-2.22}=0.45\)
Since E is on the Y-axis, we know that the intercept is 10. Plugging these values into the line equation, the line we need is described by the equation
\(y = 0.45x + 10\)
This is one of the ways a line can be defined and so we have solved the problem. If we wanted to plot the line, we would find another point on the line using the equation and then draw the line through that point and the intercept.
Intersection of two straight lines
The point of intersection of two non-parallel lines can be found from the equations of the two lines.
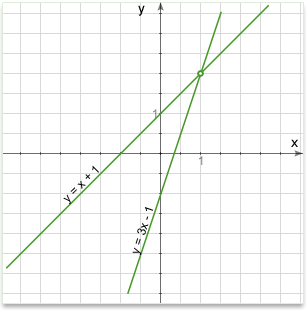
To find the intersection of two straight lines:
1. First we need their equations
2. Then, since at the point of intersection, the two equations will share a point and thus have the same values of x and y, we set the two equations equal to each other. This gives an equation that we can solve for x
3. We substitute the x value in one of the line equations (it doesn't matter which) and solve it for y.
This gives us the x and y coordinates of the intersection.
Example #1
Q: Find the point of intersection of two lines that have the following equations (in slope-intercept form):
\(y = 3x-3\)
\(y = 2.3x+4\)
Solution: At the point of intersection they will both have the same y-coordinate value, so we set the equations equal to each other:
\(3x-3 = 2.3x+4\)
This gives us an equation in one unknown (x) which we can solve:
\(x = 10\)
To find y, simply set x equal to 10 in the equation of either line and solve for y:
Equation for a line \(y = 3x - 3\) (Either line will do)
Set x equal to 10: \(y = 30 - 3\)
\(y = 27\)
We now have both x and y, so the intersection point is (10, 27)
Example #2
Q: Find the point of intersection of two lines that have the following equations (in slope-intercept form): \(y = 3x-3\) and \(x = 12\) (A vertical line)
Solution: When one of the lines is vertical, it has no defined slope. We find the intersection slightly differently.
On the vertical line, all points on it have an x-coordinate of 12 (the definition of a vertical line), so we simply set x equal to 12 in the first equation and solve it for y.
Equation for a line \(y = 3x - 3\)
Set x equal to 12 \(y = 36 - 3\)
\(y = 33\)
So the intersection point is at (12,33).
Note: If both lines are vertical or horizontal, they are parallel and have no intersection
Distance from a point to a line
The distance from a point to a line is the shortest distance between them - the length of a perpendicular line segment from the line to the point.
The distance from a point \((x_0, y_0)\) to a line \(ax+by+c=0\) is given by the formula:
\(D=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
Circle on a plane
In an x-y Cartesian coordinate system, the circle with center (a, b) and radius r is the set of all points (x, y) such that:
\((x-a)^2+(y-b)^2=r^2\)
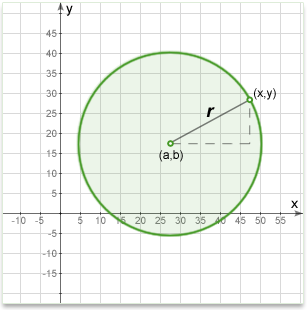
This equation of the circle follows from the Pythagorean theorem applied to any point on the circle: as shown in the diagram above, the radius is the hypotenuse of a right-angled triangle whose other sides are of length x-a and y-b.
If the circle is centered at the origin (0, 0), then the equation simplifies to:
\(x^2+y^2=r^2\)
Number line
A number line is a picture of a straight line on which every point corresponds to a real number and every real number to a point.

On the GMAT we can often see such statement: \(k\) is halfway between \(m\) and \(n\) on the number line. Remember this statement can ALWAYS be expressed as:
\(\frac{m+n}{2}=k\).
Also on the GMAT we can often see another statement: The distance between \(p\) and \(m\) on the number line is the same as the distance between \(p\) and \(n\). Remember this statement can ALWAYS be expressed as:
\(|p-m|=|p-n|\).
Parabola
A parabola is the graph associated with a quadratic function, i.e. a function of the form \(y=ax^2+bx+c\).
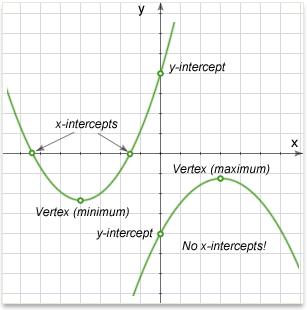
The general or standard form of a quadratic function is \(y =ax^2+bx+c\), or in function form, \(f(x)=ax^2+bx+c\), where \(x\) is the independent variable, \(y\) is the dependent variable, and \(a\), \(b\), and \(c\) are constants.
x-intercepts: The x-intercepts, if any, are also called the roots of the function. The x-intercepts are the solutions to the equation \(0=ax^2+bx+c\) and can be calculated by the formula:
\(x_1=\frac{-b-\sqrt{b^2-4ac}}{2a}\) and \(x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}\)
Expression \(b^2-4ac\) is called discriminant:
y-intercept: Given \(y =ax^2+bx+c\), the y-intercept is \(c\), as y intercept means the value of y when x=0.
Vertex: The vertex represents the maximum (or minimum) value of the function, and is very important in calculus.
The vertex of the parabola is located at point \((-\frac{b}{2a},\) \(c-\frac{b^2}{4a})\).
Note: typically just \(-\frac{b}{2a},\) is calculated and plugged in for x to find y.
More on Coordinate Geometry Under the Spoiler
For other subjects:
ALL YOU NEED FOR QUANT ! ! !
Ultimate GMAT Quantitative Megathread
Practice Questions
Easy:
1. https://gmatclub.com/forum/which-of-the ... 29938.html
2. https://gmatclub.com/forum/in-the-recta ... 65534.html
3. https://gmatclub.com/forum/in-a-rectang ... 94392.html
4. https://gmatclub.com/forum/in-the-xy-pl ... 05023.html
5. https://gmatclub.com/forum/in-the-figur ... 68654.html
6. https://gmatclub.com/forum/in-the-xy-pl ... 30899.html
7. https://gmatclub.com/forum/in-the-xy-pl ... 21712.html
8. https://gmatclub.com/forum/in-the-xy-pl ... 40727.html
9. https://gmatclub.com/forum/if-each-of-t ... 20583.html
10. https://gmatclub.com/forum/in-the-xy-pl ... 93838.html
11. https://gmatclub.com/forum/in-the-line- ... 31295.html
Medium:
1. https://gmatclub.com/forum/which-of-the ... 55961.html
2. https://gmatclub.com/forum/line-m-lies- ... 98105.html
3. https://gmatclub.com/forum/in-the-coord ... 67670.html
4. https://gmatclub.com/forum/in-the-coord ... 44795.html
5. https://gmatclub.com/forum/in-the-xy-co ... 07226.html
6. https://gmatclub.com/forum/in-the-recta ... 20818.html
7. https://gmatclub.com/forum/on-the-graph ... 36560.html
8. https://gmatclub.com/forum/in-the-xy-pl ... 42863.html
9. https://gmatclub.com/forum/the-graph-of ... 07199.html
10. https://gmatclub.com/forum/in-the-xy-co ... 35012.html
Hard:
1. https://gmatclub.com/forum/right-triang ... 71597.html
2. https://gmatclub.com/forum/for-every-po ... 91527.html
3. https://gmatclub.com/forum/point-1-0-is ... 82265.html
4. https://gmatclub.com/forum/if-equation- ... 01963.html
5. https://gmatclub.com/forum/in-the-recta ... 44774.html
6. https://gmatclub.com/forum/in-the-xy-pl ... 26463.html
7. https://gmatclub.com/forum/in-the-figur ... 39117.html
8. https://gmatclub.com/forum/the-graph-of ... 07473.html
9. https://gmatclub.com/forum/the-center-o ... 89027.html
10. https://gmatclub.com/forum/in-the-xy-pl ... 00739.html

Math_cg_7.png [ 6.78 KiB | Viewed 860168 times ]

Math_cg_3.png [ 7.48 KiB | Viewed 865497 times ]

Math_cg_20.png [ 18.71 KiB | Viewed 874117 times ]

Math_cg_19.png [ 1.78 KiB | Viewed 850885 times ]

Math_cg_18.png [ 17.71 KiB | Viewed 950923 times ]

Math_cg_17.png [ 8.18 KiB | Viewed 854514 times ]

Math_cg_16.png [ 14.51 KiB | Viewed 854850 times ]

Math_cg_15.png [ 11.41 KiB | Viewed 854819 times ]

Math_cg_14.png [ 10.13 KiB | Viewed 855132 times ]

Math_cg_13.png [ 12.3 KiB | Viewed 855602 times ]

Math_cg_12.png [ 10.15 KiB | Viewed 855941 times ]

Math_cg_11.png [ 7.25 KiB | Viewed 856068 times ]

Math_cg_10.png [ 7.68 KiB | Viewed 856544 times ]

Math_cg_9.png [ 17.16 KiB | Viewed 869323 times ]

Math_cg_8.png [ 9.5 KiB | Viewed 869007 times ]

Math_cg_6.png [ 9.74 KiB | Viewed 860311 times ]

Math_cg_5.png [ 9.59 KiB | Viewed 860418 times ]

Math_cg_4.png [ 6.94 KiB | Viewed 862528 times ]

Math_cg_2.png [ 8.04 KiB | Viewed 870049 times ]

Math_cg_1.png [ 10.01 KiB | Viewed 866277 times ]

Math_icon_cg.png [ 3.22 KiB | Viewed 857749 times ]
created by: Bunuel
edited by: bb, walker
Definition
Coordinate geometry, or Cartesian geometry, is the study of geometry using a coordinate system and the principles of algebra and analysis.
The Coordinate Plane
In coordinate geometry, points are placed on the "coordinate plane" as shown below. The coordinate plane is a two-dimensional surface on which we can plot points, lines and curves. It has two scales, called the x-axis and y-axis, at right angles to each other. The plural of axis is 'axes' (pronounced "AXE-ease").
A point's location on the plane is given by two numbers, one that tells where it is on the x-axis and another which tells where it is on the y-axis. Together, they define a single, unique position on the plane. So in the diagram above, the point A has an x value of 20 and a y value of 15. These are the coordinates of the point A, sometimes referred to as its "rectangular coordinates".
X axis
The horizontal scale is called the x-axis and is usually drawn with the zero point in the middle. Values to the right are positive and those to the left are negative.
Y axis
The vertical scale is called the y-axis and is also usually drawn with the zero point in the middle. Values above the origin are positive and those below are negative.
Origin
The point where the two axes cross (at zero on both scales) is called the origin.
Quadrants
When the origin is in the center of the plane, they divide it into four areas called quadrants.
The first quadrant, by convention, is the top right, and then they go around counter-clockwise. In the diagram above they are labeled Quadrant 1, 2 etc. It is conventional to label them with numerals but we talk about them as "first, second, third, and fourth quadrant".
Point (x,y)
The coordinates are written as an "ordered pair". The letter P is simply the name of the point and is used to distinguish it from others.
The two numbers in parentheses are the x and y coordinate of the point. The first number (x) specifies how far along the x (horizontal) axis the point is. The second is the y coordinate and specifies how far up or down the y axis to go. It is called an ordered pair because the order of the two numbers matters - the first is always the x (horizontal) coordinate.
The sign of the coordinate is important. A positive number means to go to the right (x) or up (y). Negative numbers mean to go left (x) or down (y).
Distance between two points
Given coordinates of two points, distance D between two points is given by:
\(D=\sqrt{dx^2+dy^2}\) (where \(dx\) is the difference between the x-coordinates and \(dy\) is the difference between the y-coordinates of the points)
As you can see, the distance formula on the plane is derived from the Pythagorean theorem.
Above formula can be written in the following way for given two points \((x_1,y_1)\) and \((x_2,y_2)\):
\(D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Vertical and horizontal lines
If the line segment is exactly vertical or horizontal, the formula above will still work fine, but there is an easier way. For a horizontal line, its length is the difference between the x-coordinates. For a vertical line its length is the difference between the y-coordinates.
Distance between the point A (x,y) and the origin
As the one point is origin with coordinate O (0,0) the formula can be simplified to:
\(D=\sqrt{x^2+y^2}\)
Example #1
Q: Find the distance between the point A (3,-1) and B (-1,2)
Solution: Substituting values in the equation we'll get
\(D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
\(D=\sqrt{(-1-3)^2+(2-(-1))^2}=\sqrt{16+9}=5\)
Midpoint of a Line Segment
A line segment on the coordinate plane is defined by two endpoints whose coordinates are known. The midpoint of this line is exactly halfway between these endpoints and it's location can be found using the Midpoint Theorem, which states:
• The x-coordinate of the midpoint is the average of the x-coordinates of the two endpoints.
• Likewise, the y-coordinate is the average of the y-coordinates of the endpoints.
Coordinates of the midpoint \(M (x_m,y_m)\) of the line segment AB, (\(A (x_1,y_1)\) and \(B (x_2,y_2)\)) are \(x_m=\frac{x_1+x_2}{2}\) and \(y_m=\frac{y_1+y_2}{2}\)
Lines in Coordinate Geometry
In Euclidean geometry, a line is a straight curve. In coordinate geometry, lines in a Cartesian plane can be described algebraically by linear equations and linear functions.
Every straight line in the plane can represented by a first degree equation with two variables.
There are several approaches commonly used in coordinate geometry. It does not matter whether we are talking about a line, ray or line segment. In all cases any of the below methods will provide enough information to define the line exactly.
1. General form.
The general form of the equation of a straight line is
\(ax+by+c=0\)
Where \(a\), \(b\) and \(c\) are arbitrary constants. This form includes all other forms as special cases. For an equation in this form the slope is \(-\frac{a}{b}\) and the y intercept is \(-\frac{c}{b}\).
2. Point-intercept form.
\(y=mx+b\)
Where: \(m\) is the slope of the line; \(b\) is the y-intercept of the line; \(x\) is the independent variable of the function \(y\).
3. Using two points
In figure below, a line is defined by the two points A and B. By providing the coordinates of the two points, we can draw a line. No other line could pass through both these points and so the line they define is unique.
The equation of a straight line passing through points \(P_1(x_1, y_1)\) and \(P_2(x_2, y_2)\) is:
\(\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}\)
Example #1
Q: Find the equation of a line passing through the points A (17,4) and B (9,9).
Solution: Substituting the values in equation \(\frac{y-y_1}{x-x_1}=\frac{y_1-y_2}{x_1-x_2}\) we'll get: \(\frac{y-4}{x-17}=\frac{4-9}{17-9}\)
\(\frac{y-4}{x-17}=\frac{-5}{8}\) --> \(8y-32=-5x+85\) --> \(8y+5x-117=0\) OR if we want to write the equation in the slope-intercept form: \(y=-\frac{5}{8}x+\frac{117}{8}\)
4. Using one point and the slope
Sometimes on the GMAT you will be given a point on the line and its slope and from this information you will need to find the equation or check if this line goes through another point. You can think of the slope as the direction of the line. So once you know that a line goes through a certain point, and which direction it is pointing, you have defined one unique line.
In figure below, we see a line passing through the point A at (14,23). We also see that it's slope is +2 (which means it goes 2 up for every one across). With these two facts we can establish a unique line.
The equation of a straight line that passes through a point \(P_1(x_1, y_1)\) with a
slope m is:
\(y-y_1=m(x-x_1)\)
Example #2
Q: Find the equation of a line passing through the point A (14,23) and the slope 2.
Solution: Substituting the values in equation \(y-y_1=m(x-x_1)\) we'll get \(y-23=2(x-14)\) --> \(y=2x-5\)
4. Intercept form.
The equation of a straight line whose x and y intercepts are a and b, respectively, is:
\(\frac{x}{a}+\frac{y}{b}=1\)
Example #3
Q: Find the equation of a line whose x intercept is 5 and y intercept is 2.
Solution: Substituting the values in equation \(\frac{x}{a}+\frac{y}{b}=1\) we'll get \(\frac{x}{5}+\frac{y}{2}=1\) --> \(5y+2x-10=0\) OR if we want to write the equation in the slope-intercept form: \(y=-\frac{2}{5}x+2\)
Slope of a Line
The slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline.
The slope is defined as the ratio of the "rise" divided by the "run" between two points on a line, or in other words, the ratio of the altitude change to the horizontal distance between any two points on the line.
Given two points \((x_1,y_1)\) and \((x_2,y_2)\) on a line, the slope \(m\) of the line is:
\(m=\frac{y_2-y_1}{x_2-x_1}\)
If the equation of the line is given in the Point-intercept form: \(y=mx+b\), then \(m\) is the slope. This form of a line's equation is called the slope-intercept form, because \(b\) can be interpreted as the y-intercept of the line, the y-coordinate where the line intersects the y-axis.
If the equation of the line is given in the General form:\(ax+by+c=0\), then the slope is \(-\frac{a}{b}\) and the y intercept is \(-\frac{c}{b}\).
SLOPE DIRECTION
The slope of a line can be positive, negative, zero or undefined.
Positive slope
Here, y increases as x increases, so the line slopes upwards to the right. The slope will be a positive number. The line below has a slope of about +0.3, it goes up about 0.3 for every step of 1 along the x-axis.
Negative slope
Here, y decreases as x increases, so the line slopes downwards to the right. The slope will be a negative number. The line below has a slope of about -0.3, it goes down about 0.3 for every step of 1 along the x-axis.
Zero slope
Here, y does not change as x increases, so the line in exactly horizontal. The slope of any horizontal line is always zero. The line below goes neither up nor down as x increases, so its slope is zero.
Undefined slope
When the line is exactly vertical, it does not have a defined slope. The two x coordinates are the same, so the difference is zero. The slope calculation is then something like \(slope=\frac{15}{0}\) When you divide anything by zero the result has no meaning. The line above is exactly vertical, so it has no defined slope.
SLOPE AND QUADRANTS:
1. If the slope of a line is negative, the line WILL intersect quadrants II and IV. X and Y intercepts of the line with negative slope have the same sign. Therefore if X and Y intersects are positive, the line intersects quadrant I; if negative, quadrant III.
2. If the slope of line is positive, line WILL intersect quadrants I and III. Y and X intercepts of the line with positive slope have opposite signs. Therefore if X intersect is negative, line intersects the quadrant II too, if positive quadrant IV.
3. Every line (but the one crosses origin OR parallel to X or Y axis OR X and Y axis themselves) crosses three quadrants. Only the line which crosses origin \((0,0)\) OR is parallel to either of axis crosses only two quadrants.
4. If a line is horizontal it has a slope of \(0\), is parallel to X-axis and crosses quadrant I and II if the Y intersect is positive OR quadrants III and IV, if the Y intersect is negative. Equation of such line is y=b, where b is y intersect.
5. If a line is vertical, the slope is not defined, line is parallel to Y-axis and crosses quadrant I and IV, if the X intersect is positive and quadrant II and III, if the X intersect is negative. Equation of such line is \(x=a\), where a is x-intercept.
6. For a line that crosses two points \((x_1,y_1)\) and \((x_2,y_2)\), slope \(m=\frac{y_2-y_1}{x_2-x_1}\)
7. If the slope is 1 the angle formed by the line is \(45\) degrees.
8. Given a point and slope, equation of a line can be found. The equation of a straight line that passes through a point \((x_1, y_1)\) with a slope \(m\) is: \(y - y_1 = m(x - x_1)\)
Vertical and horizontal lines
A vertical line is parallel to the y-axis of the coordinate plane. All points on the line will have the same x-coordinate.
A vertical line has no slope. Or put another way, for a vertical line the slope is undefined.
The equation of a vertical line is:
\(x=a\)
Where: x is the coordinate of any point on the line; a is where the line crosses the x-axis (x intercept). Notice that the equation is independent of y. Any point on the vertical line satisfies the equation.
A horizontal line is parallel to the x-axis of the coordinate plane. All points on the line will have the same y-coordinate.
A horizontal line has a slope of zero.
The equation of a horizontal line is:
\(y=b\)
Where: y is the coordinate of any point on the line; b is where the line crosses the y-axis (y intercept). Notice that the equation is independent of x. Any point on the horizontal line satisfies the equation.
Parallel lines
Parallel lines have the same slope.
The slope can be found using any method that is convenient to you:
From two given points on the line.
From the equation of the line in slope-intercept form
From the equation of the line in point-slope form
The equation of a line through the point \(P_1(x_1, y_1)\) and parallel to line \(ax + by + c = 0\) is:
\(a(x - x_1) + b(y - y_1) = 0\)
Distance between two parallel lines \(y=mx+b\) and \(y=mx+c\) can be found by the formula:
\(D=\frac{|b-c|}{\sqrt{m^2+1}}\)
Example #1
Q:There are two lines. One line is defined by two points at (5,5) and (25,15). The other is defined by an equation in slope-intercept form form y = 0.52x - 2.5. Are two lines parallel?
Solution:
For the top line, the slope is found using the coordinates of the two points that define the line. \(Slope=\frac{15-5}{25-5}=0.5\)
For the lower line, the slope is taken directly from the formula. Recall that the slope intercept formula is y = mx + b, where m is the slope. So looking at the formula we see that the slope is 0.52.
So, the top one has a slope of 0.5, the lower slope is 0.52, which are not equal. Therefore, the lines are not parallel.
Example #2
Q: Define a line through a point C parallel to a line passes through the points A and B.
Solution: We first find the slope of the line AB using the same method as in the example above.
\(Slope AB=\frac{20-7}{5-30}=-0.52\)
For the line to be parallel to AB it will have the same slope, and will pass through a given point, C(12,10). We therefore have enough information to define the line by it's equation in point-slope form form:
\(y=-0.52(x-12)+10\) --> \(y=-0.52x+16.24\)
Perpendicular lines
For one line to be perpendicular to another, the relationship between their slopes has to be negative reciprocal \(-\frac{1}{m}\). In other words, the two lines are perpendicular if and only if the product of their slopes is \(-1\).
The two lines \(a_1x + b_1y + c_1 = 0\) and \(a_2x + b_2y + c_2 = 0\) are perpendicular if \(a_1a_2 + b_1b_2 = 0\).
The equation of a line passing through the point \(P_1(x_1, y_1\)) and perpendicular to line \(ax + by + c = 0\) is:
\(b(x - x_1)-a(y - y_1) = 0\)
Example #1:
Q: Are the two lines below perpendicular?
Solution:
To answer, we must find the slope of each line and then check to see if one slope is the negative reciprocal of the other or if their product equals to -1.
\(Slope AB=\frac{5-19}{9-48}=\frac{-14}{-39}=0.358\)
\(Slope CD=\frac{24-4}{22-31}=\frac{20}{-9}=-2.22\)
If the lines are perpendicular, each will be the negative reciprocal of the other. It doesn't matter which line we start with, so we will pick AB:
Negative reciprocal of 0.358 is \(-\frac{1}{0.358}=-2.79\)
So, the slope of CD is -2.22, and the negative reciprocal of the slope of AB is -2.79. These are not the same, so the lines are not perpendicular, even though they may look as though they are. However, if you looked carefully at the diagram, you might have noticed that point C is a little too far to the left for the lines to be perpendicular.
Example # 2.
Q: Define a line passing through the point E and perpendicular to a line passing through the points C and D on the graph above.
Solution: The point E is on the y-axis and so is the y-intercept of the desired line. Once we know the slope of the line, we can express it using its equation in slope-intercept form y=mx+b, where m is the slope and b is the y-intercept.
First find the slope of line CD:
\(Slope CD=\frac{24-4}{22-31}=\frac{20}{-9}=-2.22\)
The line we seek will have a slope which is the negative reciprocal of:
\(-\frac{1}{-2.22}=0.45\)
Since E is on the Y-axis, we know that the intercept is 10. Plugging these values into the line equation, the line we need is described by the equation
\(y = 0.45x + 10\)
This is one of the ways a line can be defined and so we have solved the problem. If we wanted to plot the line, we would find another point on the line using the equation and then draw the line through that point and the intercept.
Intersection of two straight lines
The point of intersection of two non-parallel lines can be found from the equations of the two lines.
To find the intersection of two straight lines:
1. First we need their equations
2. Then, since at the point of intersection, the two equations will share a point and thus have the same values of x and y, we set the two equations equal to each other. This gives an equation that we can solve for x
3. We substitute the x value in one of the line equations (it doesn't matter which) and solve it for y.
This gives us the x and y coordinates of the intersection.
Example #1
Q: Find the point of intersection of two lines that have the following equations (in slope-intercept form):
\(y = 3x-3\)
\(y = 2.3x+4\)
Solution: At the point of intersection they will both have the same y-coordinate value, so we set the equations equal to each other:
\(3x-3 = 2.3x+4\)
This gives us an equation in one unknown (x) which we can solve:
\(x = 10\)
To find y, simply set x equal to 10 in the equation of either line and solve for y:
Equation for a line \(y = 3x - 3\) (Either line will do)
Set x equal to 10: \(y = 30 - 3\)
\(y = 27\)
We now have both x and y, so the intersection point is (10, 27)
Example #2
Q: Find the point of intersection of two lines that have the following equations (in slope-intercept form): \(y = 3x-3\) and \(x = 12\) (A vertical line)
Solution: When one of the lines is vertical, it has no defined slope. We find the intersection slightly differently.
On the vertical line, all points on it have an x-coordinate of 12 (the definition of a vertical line), so we simply set x equal to 12 in the first equation and solve it for y.
Equation for a line \(y = 3x - 3\)
Set x equal to 12 \(y = 36 - 3\)
\(y = 33\)
So the intersection point is at (12,33).
Note: If both lines are vertical or horizontal, they are parallel and have no intersection
Distance from a point to a line
The distance from a point to a line is the shortest distance between them - the length of a perpendicular line segment from the line to the point.
The distance from a point \((x_0, y_0)\) to a line \(ax+by+c=0\) is given by the formula:
\(D=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
- When the line is horizontal the formula transforms to: \(D=|P_y-L_y|\)
Where: \(P_y\) is the y-coordinate of the given point P; \(L_y\) is the y-coordinate of any point on the given vertical line L. | | the vertical bars mean "absolute value" - make it positive even if it calculates to a negative. - When the line is vertical the formula transforms to: \(D=|P_x-L_x|\)
Where: \(P_x\) is the x-coordinate of the given point P; \(L_x\) is the x-coordinate of any point on the given vertical line L. | | the vertical bars mean "absolute value" - make it positive even if it calculates to a negative. - When the given point is origin, then the distance between origin and line ax+by+c=0 is given by the formula:
\(D=\frac{|c|}{\sqrt{a^2+b^2}}\)
Circle on a plane
In an x-y Cartesian coordinate system, the circle with center (a, b) and radius r is the set of all points (x, y) such that:
\((x-a)^2+(y-b)^2=r^2\)
This equation of the circle follows from the Pythagorean theorem applied to any point on the circle: as shown in the diagram above, the radius is the hypotenuse of a right-angled triangle whose other sides are of length x-a and y-b.
If the circle is centered at the origin (0, 0), then the equation simplifies to:
\(x^2+y^2=r^2\)
Number line
A number line is a picture of a straight line on which every point corresponds to a real number and every real number to a point.
On the GMAT we can often see such statement: \(k\) is halfway between \(m\) and \(n\) on the number line. Remember this statement can ALWAYS be expressed as:
\(\frac{m+n}{2}=k\).
Also on the GMAT we can often see another statement: The distance between \(p\) and \(m\) on the number line is the same as the distance between \(p\) and \(n\). Remember this statement can ALWAYS be expressed as:
\(|p-m|=|p-n|\).
Parabola
A parabola is the graph associated with a quadratic function, i.e. a function of the form \(y=ax^2+bx+c\).
The general or standard form of a quadratic function is \(y =ax^2+bx+c\), or in function form, \(f(x)=ax^2+bx+c\), where \(x\) is the independent variable, \(y\) is the dependent variable, and \(a\), \(b\), and \(c\) are constants.
- The larger the absolute value of \(a\), the steeper (or thinner) the parabola is, since the value of y is increased more quickly.
- If \(a\) is positive, the parabola opens upward, if negative, the parabola opens downward.
x-intercepts: The x-intercepts, if any, are also called the roots of the function. The x-intercepts are the solutions to the equation \(0=ax^2+bx+c\) and can be calculated by the formula:
\(x_1=\frac{-b-\sqrt{b^2-4ac}}{2a}\) and \(x_2=\frac{-b+\sqrt{b^2-4ac}}{2a}\)
Expression \(b^2-4ac\) is called discriminant:
- If discriminant is positive parabola has two intercepts with x-axis;
- If discriminant is negative parabola has no intercepts with x-axis;
- If discriminant is zero parabola has one intercept with x-axis (tangent point).
y-intercept: Given \(y =ax^2+bx+c\), the y-intercept is \(c\), as y intercept means the value of y when x=0.
Vertex: The vertex represents the maximum (or minimum) value of the function, and is very important in calculus.
The vertex of the parabola is located at point \((-\frac{b}{2a},\) \(c-\frac{b^2}{4a})\).
Note: typically just \(-\frac{b}{2a},\) is calculated and plugged in for x to find y.
More on Coordinate Geometry Under the Spoiler
Show SpoilerMore on Coordinate Geometry Under the Spoiler
24. Coordinate Geometry
- Theory
- Questions
Math: Coordinate Geometry
Beauty of Coordinate geometry
Dealing with Tangents on the GMAT
DS Questions
PS Questions
For other subjects:
ALL YOU NEED FOR QUANT ! ! !
Ultimate GMAT Quantitative Megathread
Practice Questions
Easy:
1. https://gmatclub.com/forum/which-of-the ... 29938.html
2. https://gmatclub.com/forum/in-the-recta ... 65534.html
3. https://gmatclub.com/forum/in-a-rectang ... 94392.html
4. https://gmatclub.com/forum/in-the-xy-pl ... 05023.html
5. https://gmatclub.com/forum/in-the-figur ... 68654.html
6. https://gmatclub.com/forum/in-the-xy-pl ... 30899.html
7. https://gmatclub.com/forum/in-the-xy-pl ... 21712.html
8. https://gmatclub.com/forum/in-the-xy-pl ... 40727.html
9. https://gmatclub.com/forum/if-each-of-t ... 20583.html
10. https://gmatclub.com/forum/in-the-xy-pl ... 93838.html
11. https://gmatclub.com/forum/in-the-line- ... 31295.html
Medium:
1. https://gmatclub.com/forum/which-of-the ... 55961.html
2. https://gmatclub.com/forum/line-m-lies- ... 98105.html
3. https://gmatclub.com/forum/in-the-coord ... 67670.html
4. https://gmatclub.com/forum/in-the-coord ... 44795.html
5. https://gmatclub.com/forum/in-the-xy-co ... 07226.html
6. https://gmatclub.com/forum/in-the-recta ... 20818.html
7. https://gmatclub.com/forum/on-the-graph ... 36560.html
8. https://gmatclub.com/forum/in-the-xy-pl ... 42863.html
9. https://gmatclub.com/forum/the-graph-of ... 07199.html
10. https://gmatclub.com/forum/in-the-xy-co ... 35012.html
Hard:
1. https://gmatclub.com/forum/right-triang ... 71597.html
2. https://gmatclub.com/forum/for-every-po ... 91527.html
3. https://gmatclub.com/forum/point-1-0-is ... 82265.html
4. https://gmatclub.com/forum/if-equation- ... 01963.html
5. https://gmatclub.com/forum/in-the-recta ... 44774.html
6. https://gmatclub.com/forum/in-the-xy-pl ... 26463.html
7. https://gmatclub.com/forum/in-the-figur ... 39117.html
8. https://gmatclub.com/forum/the-graph-of ... 07473.html
9. https://gmatclub.com/forum/the-center-o ... 89027.html
10. https://gmatclub.com/forum/in-the-xy-pl ... 00739.html
Show SpoilerImages
Attachment:
Math_cg_7.png [ 6.78 KiB | Viewed 860168 times ]
Attachment:
Math_cg_3.png [ 7.48 KiB | Viewed 865497 times ]
Attachment:
Math_cg_20.png [ 18.71 KiB | Viewed 874117 times ]
Attachment:
Math_cg_19.png [ 1.78 KiB | Viewed 850885 times ]
Attachment:
Math_cg_18.png [ 17.71 KiB | Viewed 950923 times ]
Attachment:
Math_cg_17.png [ 8.18 KiB | Viewed 854514 times ]
Attachment:
Math_cg_16.png [ 14.51 KiB | Viewed 854850 times ]
Attachment:
Math_cg_15.png [ 11.41 KiB | Viewed 854819 times ]
Attachment:
Math_cg_14.png [ 10.13 KiB | Viewed 855132 times ]
Attachment:
Math_cg_13.png [ 12.3 KiB | Viewed 855602 times ]
Attachment:
Math_cg_12.png [ 10.15 KiB | Viewed 855941 times ]
Attachment:
Math_cg_11.png [ 7.25 KiB | Viewed 856068 times ]
Attachment:
Math_cg_10.png [ 7.68 KiB | Viewed 856544 times ]
Attachment:
Math_cg_9.png [ 17.16 KiB | Viewed 869323 times ]
Attachment:
Math_cg_8.png [ 9.5 KiB | Viewed 869007 times ]
Attachment:
Math_cg_6.png [ 9.74 KiB | Viewed 860311 times ]
Attachment:
Math_cg_5.png [ 9.59 KiB | Viewed 860418 times ]
Attachment:
Math_cg_4.png [ 6.94 KiB | Viewed 862528 times ]
Attachment:
Math_cg_2.png [ 8.04 KiB | Viewed 870049 times ]
Attachment:
Math_cg_1.png [ 10.01 KiB | Viewed 866277 times ]
Attachment:
Math_icon_cg.png [ 3.22 KiB | Viewed 857749 times ]
Kudos
Bookmarks
There's one formula I'd like to add to the list:
Area of a triangle given the three vertices of the triangle (\(x1, y1\)), (\(x2, y2\)) and (\(x3, y3\))
\(A = \frac{1}{2} * [x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]\)
To remember the order of variables just remember 1,2,3 then 2,3,1 and 3,1,2.
This would be useful in coordinate geometry in case the triangle does not rest on one of the axes and you know the three vertices.
Area of a triangle given the three vertices of the triangle (\(x1, y1\)), (\(x2, y2\)) and (\(x3, y3\))
\(A = \frac{1}{2} * [x1(y2-y3) + x2(y3-y1) + x3(y1-y2)]\)
To remember the order of variables just remember 1,2,3 then 2,3,1 and 3,1,2.
This would be useful in coordinate geometry in case the triangle does not rest on one of the axes and you know the three vertices.
Kudos
Bookmarks
This has to be my favorite sentence: "In Euclidean geometry, a line is a straight curve. In coordinate geometry, lines in a Cartesian plane can be described algebraically by linear equations and linear functions."










