Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth
Kudos
Bookmarks
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
(N/A)
Question Stats:
0% (00:00) correct 0% (00:00) wrong
0% (00:00) wrong  based on 0 sessions
based on 0 sessions
History
Date
Time
Result
Not Attempted Yet
Quantity A
The perimeter of triangle ABC
Quantity B
5
Attachment:
4.jpg [ 13.28 KiB | Viewed 199 times ]
Kudos
Bookmarks
OE
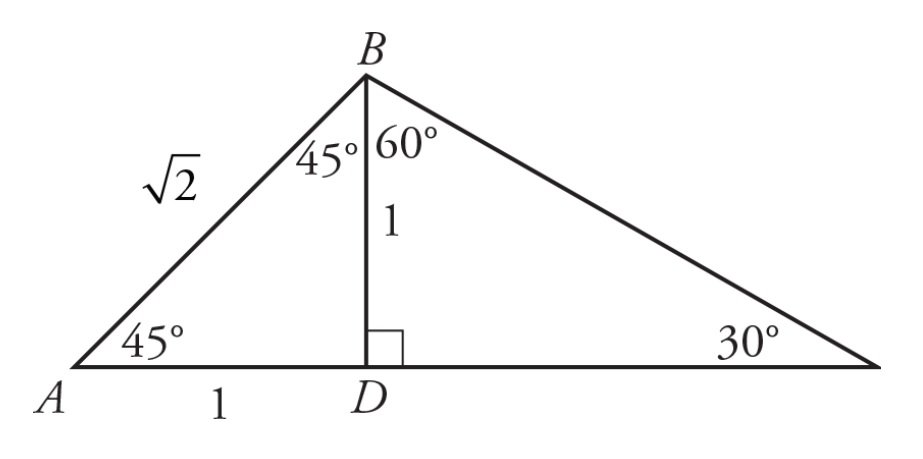
Although there seems to be very little information here, the two small triangles that comprise triangle ABC may seem familiar. First, fill in the additional angles in the diagram:

With the additional angles filled in, it is clear that the two smaller triangles are special right triangles: a 45–45–90 triangle and a 30– 60–90 triangle. You know the ratios of the side lengths for each of these triangles. For a 45–45–90 triangle, the ratio is \(x : x : x \sqrt{2}\).
In this diagram, the value of x is 1 (side BD), so AD is 1 and AB is \(\sqrt{2}\)

For a 30–60–90 triangle, the ratio is \(x : x[m]3\) : 2x[/m]. In this diagram, x is 1 (side BD), so DC is \(\sqrt{3}\) and BC is 2:

Now calculate the perimeter of triangle ABC:
Quantity A
\(1+2+\sqrt{2}+\sqrt{3}\)
Quantity B
5
Now you need to compare this sum to 5. A good approximation of \(\sqrt{2}\) is 1.4 and a good approximation of is \(\sqrt{3}\) 1.7:
In fact, simply knowing that each square root is greater than 1 would let you conclude that, Quantity A is greater.
Alternatively, you could use the calculator to compute Quantity A.

D3.jpg [ 33.46 KiB | Viewed 177 times ]
D2.jpg [ 32.09 KiB | Viewed 174 times ]

D1.jpg [ 22.34 KiB | Viewed 175 times ]
Although there seems to be very little information here, the two small triangles that comprise triangle ABC may seem familiar. First, fill in the additional angles in the diagram:
With the additional angles filled in, it is clear that the two smaller triangles are special right triangles: a 45–45–90 triangle and a 30– 60–90 triangle. You know the ratios of the side lengths for each of these triangles. For a 45–45–90 triangle, the ratio is \(x : x : x \sqrt{2}\).
In this diagram, the value of x is 1 (side BD), so AD is 1 and AB is \(\sqrt{2}\)
For a 30–60–90 triangle, the ratio is \(x : x[m]3\) : 2x[/m]. In this diagram, x is 1 (side BD), so DC is \(\sqrt{3}\) and BC is 2:
Now calculate the perimeter of triangle ABC:
Quantity A
\(1+2+\sqrt{2}+\sqrt{3}\)
Quantity B
5
Now you need to compare this sum to 5. A good approximation of \(\sqrt{2}\) is 1.4 and a good approximation of is \(\sqrt{3}\) 1.7:
In fact, simply knowing that each square root is greater than 1 would let you conclude that, Quantity A is greater.
Alternatively, you could use the calculator to compute Quantity A.
Attachment:
D3.jpg [ 33.46 KiB | Viewed 177 times ]
Attachment:
D2.jpg [ 32.09 KiB | Viewed 174 times ]
Attachment:
D1.jpg [ 22.34 KiB | Viewed 175 times ]








