|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Kudos
Bookmarks
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
(N/A)
Question Stats:
100% (00:31) correct 0% (00:00) wrong
0% (00:00) wrong  based on 1 sessions
based on 1 sessions
History
Date
Time
Result
Not Attempted Yet
Quantity A
(x + 2)(x - 2)
Quantity B
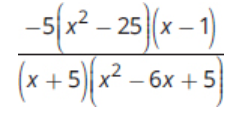
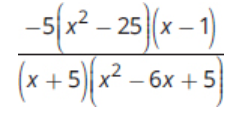
GMAT-Club-Forum-u9u48ywr.png [ 22.9 KiB | Viewed 224 times ]
(x + 2)(x - 2)
Quantity B
Attachment:
GMAT-Club-Forum-u9u48ywr.png [ 22.9 KiB | Viewed 224 times ]
Kudos
Bookmarks
Given and to find:
Solution:
Let's simplify Quantity B since that looks a lot more complex:
Finally, we need to compare (x^2 - 4) with -5.
Let's put them side by side with a '?' in between (a placeholder for = or > or <)
Correct Answer: Quantity A is greater.
Shweta Koshija
GMAT, GRE, SAT Coach for 10+ years
- Two quantities (A and B).
- We need to compare the two.
Solution:
Let's simplify Quantity B since that looks a lot more complex:
- Numerator: -5(x^2 - 25)(x - 1)
- -5(x - 5)(x + 5)(x - 1) --- Using the identity of difference of squares.
- Denominator: (x + 5)(x^2 – 6x + 5)
- We can factor x^2 – 6x + 5 into (x – 1)(x – 5)
- So, the denominator becomes (x + 5)(x – 1)(x – 5)
- Thus, Quantity B: –5(x + 5)(x – 5)(x – 1) / (x + 5)(x - 1)(x - 1)
- Canceling out the common factors, we are left with only –5
- So, Quantity B = –5
- Quantity A: (x + 2)(x – 2)
- Again, using the identity of Difference of squares, we have Quantity A = x^2 – 4
Finally, we need to compare (x^2 - 4) with -5.
Let's put them side by side with a '?' in between (a placeholder for = or > or <)
- x^2 - 4 ? - 5
- Adding 4 on both sides, this comparison is equivalent to x^2 ? -1
- Now, we are sure that x^2 is ALWAYS greater than -1.
- So, Quantity A is always greater than Quantity B.
Correct Answer: Quantity A is greater.
Shweta Koshija
GMAT, GRE, SAT Coach for 10+ years
Kudos
Bookmarks
OE
Using FOIL, Quantity A can be rewritten as \(x^2 - 4.\) Quantity B needs to be simplified. In the numerator, \(x^2 - 25\) can be factored into \((x + 5)(x - 5).\) In the denominator, \(x^2 - 6x + 5\) can be factored into \((x - 5)(x - 1).\) The fraction can then be simplified by canceling out common factors in the numerator and denominator:
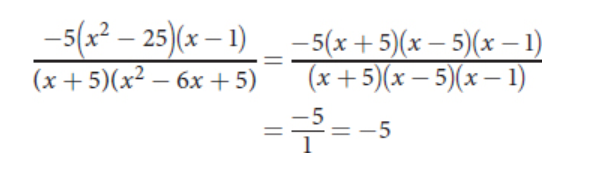
So, Quantity B is equal to -5. Without knowing what x is, it might seem that Quantity A and Quantity B cannot be compared. However, when x is squared, the result cannot be negative. The smallest value it could have is 0. Subtracting 4, the smallest possible value of Quantity A is -4. That means Quantity A must be greater than or equal to -4. Any such number will always be greater than -5, so Quantity A will always be greater than Quantity B, no matter what x is. That makes (A) the correct answer.
Answer: A
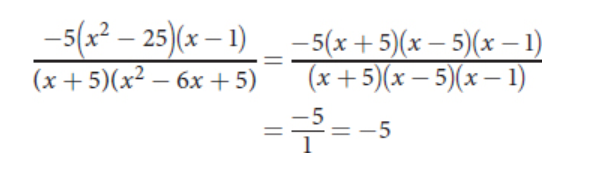
GMAT-Club-Forum-xl54r2e7.png [ 49.98 KiB | Viewed 159 times ]
Using FOIL, Quantity A can be rewritten as \(x^2 - 4.\) Quantity B needs to be simplified. In the numerator, \(x^2 - 25\) can be factored into \((x + 5)(x - 5).\) In the denominator, \(x^2 - 6x + 5\) can be factored into \((x - 5)(x - 1).\) The fraction can then be simplified by canceling out common factors in the numerator and denominator:
So, Quantity B is equal to -5. Without knowing what x is, it might seem that Quantity A and Quantity B cannot be compared. However, when x is squared, the result cannot be negative. The smallest value it could have is 0. Subtracting 4, the smallest possible value of Quantity A is -4. That means Quantity A must be greater than or equal to -4. Any such number will always be greater than -5, so Quantity A will always be greater than Quantity B, no matter what x is. That makes (A) the correct answer.
Answer: A
Attachment:
GMAT-Club-Forum-xl54r2e7.png [ 49.98 KiB | Viewed 159 times ]








