|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Kudos
Bookmarks
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
(N/A)
Question Stats:
0% (00:00) correct 100% (02:29) wrong
100% (02:29) wrong  based on 2 sessions
based on 2 sessions
History
Date
Time
Result
Not Attempted Yet
Set A has 50 members and set B has 53 members. At least 2 of the members in set A are not in set B. Which of the following could be the number of members in set B that are not in set A ?
Indicate all such numbers.
A. 3
B. 5
C. 13
D. 25
E. 50
F. 53
Indicate all such numbers.
A. 3
B. 5
C. 13
D. 25
E. 50
F. 53
ShowHide Answer
Official Answer
B,C,D,E,F
Kudos
Bookmarks
OE
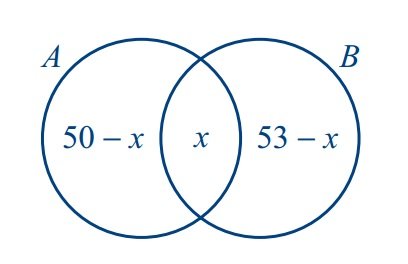
Let x be the number of members in the intersection of set A and set B. Ten the distribution of the members of A and B can be represented by the following Venn diagram.

The question asks you to indicate which of the answer choices could be the number of members in set B that are not in set A. Tis is equivalent to determining which of the answer choices are possible values of 53 - x.
You are given that the number of members in set A that are not in set B is at least 2, and clearly the number of members in set A that are not in set B is at most all 50 members of A; that is, 2 ≤ 50 - x ≤ 50. Note that 53 - x is 3 more than 50 - x. So by adding 3 to each part of 2 ≤ 50 - x ≤ 50, you get the equivalent inequality 5 ≤ 53 - x ≤ 53. Thus the number of members in set B that are not in set A can be any integer from 5 to 53. Te correct answer consists of Choices B, C, D, E, and F.
3.jpg [ 19.64 KiB | Viewed 302 times ]
Let x be the number of members in the intersection of set A and set B. Ten the distribution of the members of A and B can be represented by the following Venn diagram.
The question asks you to indicate which of the answer choices could be the number of members in set B that are not in set A. Tis is equivalent to determining which of the answer choices are possible values of 53 - x.
You are given that the number of members in set A that are not in set B is at least 2, and clearly the number of members in set A that are not in set B is at most all 50 members of A; that is, 2 ≤ 50 - x ≤ 50. Note that 53 - x is 3 more than 50 - x. So by adding 3 to each part of 2 ≤ 50 - x ≤ 50, you get the equivalent inequality 5 ≤ 53 - x ≤ 53. Thus the number of members in set B that are not in set A can be any integer from 5 to 53. Te correct answer consists of Choices B, C, D, E, and F.
Attachment:
3.jpg [ 19.64 KiB | Viewed 302 times ]









