Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 20
01:30 PM EST
-02:30 PM IST
Learn how Kamakshi achieved a GMAT 675 with an impressive 96th %ile in Data Insights. Discover the unique methods and exam strategies that helped her excel in DI along with other sections for a balanced and high score. - Nov 19
12:30 PM EST
-01:30 PM EST
Learn how Keshav, a Chartered Accountant, scored an impressive 705 on GMAT in just 30 days with GMATWhiz's expert guidance. In this video, he shares preparation tips and strategies that worked for him, including the mock, time management, and more - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 24
07:00 PM PST
-08:00 PM PST
Full-length FE mock with insightful analytics, weakness diagnosis, and video explanations! - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 11 Jul 2018, 07:36.
Last edited by EgmatQuantExpert on 13 Aug 2018, 05:08, edited 5 times in total.
Last edited by EgmatQuantExpert on 13 Aug 2018, 05:08, edited 5 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
This is 2nd article in the series of article on Statistics.
You can read the previous article here: Solve any Mean and Standard deviation question under a minute !!!!
Highlights of the previous article
In the first article, we mastered the application of:
Agenda of the article
This article is intended for the students who already have a basic idea about Median and Range of a set of numbers.
In this article, we will learn how to find the maximum and minimum value of an element of any set, when we are given:
At the end of the article, we will also provide a few GMAT like practice questions to test the understanding.
So, let us see the application of Median in 3 GMAT like questions.
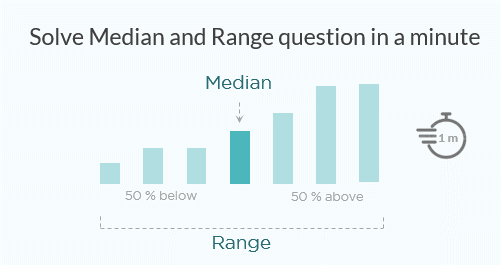
Median
So, let us read the first question.
e-GMAT Example 1
In a stack of 5 bamboo sticks, the average length of all the bamboo sticks is 55 feet and median length of all the bamboo sticks is 57 feet. If the length of the longest bamboo stick is 1 feet less than six times the length of the shortest stick, then what is the maximum possible length of the longest stick(in feet)?
Solution
From the question, we know that:
Let us continue our question again and find the maximum length of the shortest stick.
Can you see how are we applying our inferential skills??
But that is not enough ?. Once we complete this sum, you will realize how inferential skills can help us to solve a difficult problem very easily.
So, we found our answer.
But let us once write briefly what all we did in this question, so we can use the learning of this question in further questions.
Key-Takeaways from the question
Let us apply our learnings in the next question.
e-GMAT Example 2
Three friends Chris, David and Jack combined have an average weight of 75 kg and the lightest friend weigh 69 kg. What can be the minimum and maximum length value of the median weight of the three friends in kg.
Solution
In this question, we have to find the minimum and maximum value of median weight of three friends.
But, what exactly is the median of 3 numbers??
So, we have to find the minimum and maximum value of 2nd element which makes this question very much similar to the previous question.
Maximum value of median:
So, when we will get the maximum value of the median??
Minimum value of the median:
This is a very easy and simple question. ?
So, now you must have got quite a good idea to find the maximum and minimum value of an element in the questions related to median.
Let us solve one more question.
e-GMAT Example 3
The tale below gives the work experience category of 143 employees at company X and the number of employees in each category. According to the table, if ‘m’ is the median work experience of the employees at company X, then m must satisfy which of the following?
Solution
Now, this question is very tricky.
Because, if you did not read the question carefully then you might think that:
However, by close reading, you will understand that ‘m’ is the median work experience of the employees at the company X.
Key Takeaways
With these learning, let us now discuss another subtopic of statistics- Range.
Range
We know that range of a set of elements is equal to the greatest element of the set- smallest element of the set.
However, question-related to range does not always deal with finding the range of a set of given numbers.
At times we are already given the range and then we have the find the value of greatest/smallest element of the set.
Let’s understand what I am trying to say with the help of a few questions!
e-GMAT Example 4
Solution
As you can see in this question, we already know the value of range and we have to find the difference between the greatest and lowest possible value of x.
Since the range of 6, 4, 14, 3, 17, 10, and x is 16. Hence, there can be two possibilities:
Hence, the difference between greatest and lowest values of x= 19-1=18.
Now, let us solve two DS question to understand the application of range in data sufficiency.
e-GMAT Example 5
a, 13, 2, 9, b, 17
Is the range of the above given 6 numbers less than 40?
Solution
In this question, we are given 6 numbers: a, 13, 2, 9, b, 17 and we need to find their range.
Therefore, we will analyze each statement individually one by one and try to find the value of a and b.
Statement I. 5 ≤ a ≤ 20
Statement II. b = 2a
Let us combine both the statement and see if we can find the answer or not.
Combining both the statements:
So, lowest element in the series will always be 2 and greatest element can be b=40 when a=20.
Hence, the above question ends here, and we found the maximum possible value of range for a, 13, 2, 9, b, 17 by using both the statements.
But, can we find the minimum value of the range in the above example using both the statements?
Let us now move to the next question.
e-GMAT Example 6
The set S has three different numbers a, b, and c such that a<b and b<c. Is the median of set S equal to the arithmetic mean of the three numbers?
Solution
In this question, we are given:
Now, we will analyze each statement individually one by one.
Statement I. “The sum of 3 numbers of set S is equal to 3 times one of the number.”
Let us see another case.
Let us see the last case when a + b + c = 3c.
Thus, the only possible case is a + b + c = 3b and hence, a + c = 2b.
Hence, we can answer the question with the help of statement 1 alone.
Statement II. “Range of set S is equal to 2”.
Now, I want to ask did you assume b=a+1 and c=a+2??
Hence, we cannot answer the question with the help of statement 2 alone.
Thus, the correct answer is option (a).
Let us write all that we learnt from the above 3 examples related to range.
Key-Takeaways from the examples
With these learnings, we have come at the end of our article.
Key-Takeaways from the article:
Now, to imbibe all the learnings, solve all the practice questions. The link of practice questions you can find in the first comment.
To read the 1st article of statistics: Solve any Mean and Standard deviation question under a minute !!!!
Read More such articles: Must Read Articles and Practice Questions to score Q51 !!!!
To reach Q51, solve one GMAT 700 level weekly from our "Question of the week” series.
Solve any Median and Range question in a minute
This is 2nd article in the series of article on Statistics.
You can read the previous article here: Solve any Mean and Standard deviation question under a minute !!!!
Highlights of the previous article
In the first article, we mastered the application of:
- • Arithmetic Mean and applied the learnings of one simple question in a complex one.
• Standard deviation and understood the nature of standard deviation changes in 4 difference scenarios:
- o When the same number is added to all the elements of a given set.
o When the same number is subtracted from all the elements of a given set.
o When the same number is multiplied to all the elements of a given set.
o When the same number divides all the elements of a given set.
Agenda of the article
This article is intended for the students who already have a basic idea about Median and Range of a set of numbers.
In this article, we will learn how to find the maximum and minimum value of an element of any set, when we are given:
- 1. The Median of the Set OR
2. The Range of the Set.
At the end of the article, we will also provide a few GMAT like practice questions to test the understanding.
So, let us see the application of Median in 3 GMAT like questions.
Median
So, let us read the first question.
e-GMAT Example 1
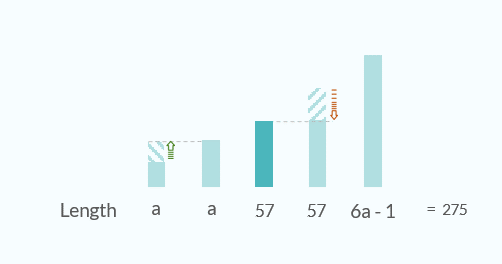
In a stack of 5 bamboo sticks, the average length of all the bamboo sticks is 55 feet and median length of all the bamboo sticks is 57 feet. If the length of the longest bamboo stick is 1 feet less than six times the length of the shortest stick, then what is the maximum possible length of the longest stick(in feet)?
Solution
From the question, we know that:
- • Average length of all the sticks = 55 feet.
- o Thus, sum of length of all the sticks = 55*5 = 275 feet
• We also know that the length of longest stick is 1 feet less than 6 times the length of the shortest stick.
- o Hence, if the length of the shortest stick is ‘a’ feet then the length of longest stick = ‘6a-1’ feet.
- • Hence, we can arrange all the sticks in the ascending order of height of the stick as
- “a, 4th longest stick, 57, 2nd longest stick, 6a-1”
- o So, we need to find the maximum value of 6a-1.
- But, when the value of 6a-1 will be longest??
- • When the value of a will be maximum, right??
• So, we need to find maximum value of ‘a’ or maximum value of the length of shortest stick.
Let us continue our question again and find the maximum length of the shortest stick.
- • So, what can be the maximum length of shortest stick?
- o Since shorter stick cannot be longer than 4th longest stick, its maximum value can only be equal to the length of the 4th longest stick.
o So, sticks can be arranged as: a, a, 57, 2nd longest stick, 6a-1.
- Now, are you thinking that this way ‘a’ can be equal to 57??
• The answer is no, a cannot be equal to 57.
• Because if a=57, then ‘6a-1’ will exceed 275 i.e. sum of the length of all the sticks which is not possible.
Can you see how are we applying our inferential skills??
But that is not enough ?. Once we complete this sum, you will realize how inferential skills can help us to solve a difficult problem very easily.
- • Now, we can write the sum of all the sticks as: a + a + 57 + 2nd longest stick + 6a-1=275
- o 8a+ 2nd longest stick = 219
o Now, we cannot go any further without knowing the value of either the length of 2nd longest stick or a.
- So, what should we do??
We should again try to visualize in terms of maximum length of shortest stick or maximum value of a.
So, when a will maximum?
- • Now, this will be easy to figure out that a will be maximum when the length of the 2nd longest stick will be minimum.
• And minimum length of 2nd longest stick can be 57 only.
- o Thus, 8a+57= 219 and a= 20.25 feet.
• Thus, maximum length of the longest stick= 6a-1= 120.25 feet.
So, we found our answer.
But let us once write briefly what all we did in this question, so we can use the learning of this question in further questions.
Key-Takeaways from the question
- • If you notice clearly then to maximize the value of ‘a’, we minimized the height of all other bamboo sticks whose lengths were not known to us.
• We first inferred that for 6a-1 to be maximum, a has to be maximum.
- o Then, we minimized the value of 4th longest bamboo stick to ‘a’ feet.
o Then, we minimized the value of 2nd longest stick to 57 for ‘a’ to be maximum.
- This gave us the maximum value of ‘a’.
• Hence, we can find the maximum value of ‘6a-1’.
Let us apply our learnings in the next question.
e-GMAT Example 2
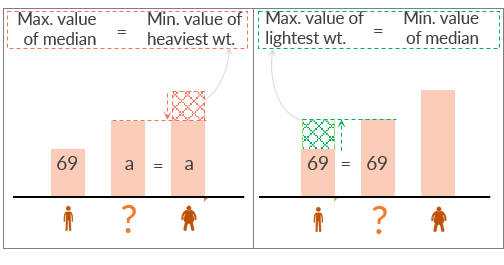
Three friends Chris, David and Jack combined have an average weight of 75 kg and the lightest friend weigh 69 kg. What can be the minimum and maximum length value of the median weight of the three friends in kg.
Solution
In this question, we have to find the minimum and maximum value of median weight of three friends.
But, what exactly is the median of 3 numbers??
- • It is the 2nd element if numbers are arranged in ascending/descending order.
So, we have to find the minimum and maximum value of 2nd element which makes this question very much similar to the previous question.
- • So, let us find the minimum and maximum value of the median one by one.
Maximum value of median:
So, when we will get the maximum value of the median??
- • If you understood the first question then you can very easily answer that for median to be maximum, the value of all other unknown variables must be minimum.
• So, if we arrange the 3 friends in the order of their weight as:
- o 69, 2nd heaviest, heaviest then we need to minimize the weight of the heaviest friend.
- And the minimum weight of heaviest friend can be equal to the 2nd heaviest friend i.e. the median weight.
If we denote median by ‘a’ then we can rearrange the 3 friends in the order of their weights as: 69, a, a
- • We are given that average weight of three friends is 75 kg.
• Hence, 69+2a= 225
- o a= 78.
• Hence, the maximum value of median weight of the three friends is 78 kg.
Minimum value of the median:
This is a very easy and simple question. ?
- • The minimum value of the median value of weight can be equal to the weight of the lightest friend i.e. 69 kg.
So, now you must have got quite a good idea to find the maximum and minimum value of an element in the questions related to median.
Let us solve one more question.
e-GMAT Example 3
The tale below gives the work experience category of 143 employees at company X and the number of employees in each category. According to the table, if ‘m’ is the median work experience of the employees at company X, then m must satisfy which of the following?
- a) m < 3
b) 3 ≤ m < 5
c) 5 ≤ m < 8
d) 8 ≤ m < 10
e) 10 ≤ m <15
Solution
Now, this question is very tricky.
Because, if you did not read the question carefully then you might think that:
- • We have to find the work experience category of median number of employees at the company X.
• And mark option C by finding the median of the number of employees.
However, by close reading, you will understand that ‘m’ is the median work experience of the employees at the company X.
- • Hence, we have to find median work experience of all the employees.
• And out of 143 employees, the median work experience will be the work experience of 143+1/2= 72nd employee.
- o Hence, we have to find the work experience of 72nd employee when all the employees are arranged in the ascending order of work experience.
• In the table given in question, all the entries are in increasing order of work experience.
- o First 23 employees have less than 3 years of work experience and next 49 employees have 3-5 years of work experience.
- So, total how many employees are there in less than 3 years and 3-5 years of work experience category.
- • 23+49=72
• Thus, option (B) is the correct answer.
Key Takeaways
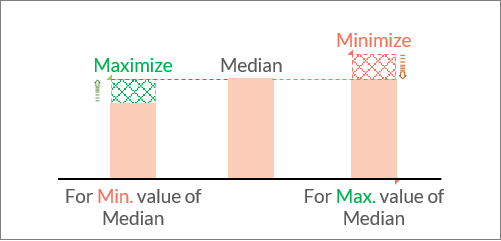
- • In the first two examples, we learnt how to find the minimum and maximum value of an element of a given set if we know the median value of the set.
- o To find the minimum value of a variable, we try to maximize the value of other variable of the set whose values are not known to us.
o And to find the maximum value of a variable, we try to minimize the value of other variable of the set whose values are not known to us.
• In the third example, we saw how important it is to read and understand the meaning of each statement of the question correctly.
With these learning, let us now discuss another subtopic of statistics- Range.
Range
We know that range of a set of elements is equal to the greatest element of the set- smallest element of the set.
However, question-related to range does not always deal with finding the range of a set of given numbers.
At times we are already given the range and then we have the find the value of greatest/smallest element of the set.
Let’s understand what I am trying to say with the help of a few questions!
e-GMAT Example 4
- If the range of 7 numbers: 6, 4, 14, 3, 17, 10, and x is 16, what is difference between the greatest and lowest possible value of x?
Solution
As you can see in this question, we already know the value of range and we have to find the difference between the greatest and lowest possible value of x.
- • Hence, we need to find the greatest and lowest possible value of x.
Since the range of 6, 4, 14, 3, 17, 10, and x is 16. Hence, there can be two possibilities:
- • 17 is the greatest element present in the set.
- o Then, 3 cannot be the lowest element as range of the 7 numbers is 16.
- Hence, x would be the lowest element.
- o And the value of x would be:
- 17-x= 16, x=1
o Hence, the lowest value of x is 1.
• 3 is the smallest element present in the set.
- o Hence, 17 cannot be the greatest element as range of the 7 numbers is 16.
- Thus, x would be the greatest element.
- x- 3 = 16
x = 19
Hence, the difference between greatest and lowest values of x= 19-1=18.
Now, let us solve two DS question to understand the application of range in data sufficiency.
e-GMAT Example 5
a, 13, 2, 9, b, 17
Is the range of the above given 6 numbers less than 40?
- 1) 5 ≤ a ≤ 20
2) b = 2a
Solution
In this question, we are given 6 numbers: a, 13, 2, 9, b, 17 and we need to find their range.
- • To find range, we need the greatest and smallest number of the set.
• And in the 6 numbers given to us, a and b are unknown.
- o So, if we can find the values of a and b, we can find the range of the: a, 13, 2, 9, b, 17
Therefore, we will analyze each statement individually one by one and try to find the value of a and b.
Statement I. 5 ≤ a ≤ 20
- Since we have no information about the value of b, we cannot answer the question with the help of statement 1 alone.
Statement II. b = 2a
- We still do not have the exact value of a and b, so we cannot conclude which number is greatest and which number is smallest among the 6 numbers.
Hence, we cannot answer the question with the help of statement 2 alone.
Let us combine both the statement and see if we can find the answer or not.
Combining both the statements:
- From statement 1, we have:
- • 5 ≤ a ≤ 20
- From statement 2, we have:
- • b = 2a
- Hence, by combining both the statements, we get:
- • 5 ≤ a ≤ 20 and 10 ≤ b ≤ 40
So, lowest element in the series will always be 2 and greatest element can be b=40 when a=20.
- • Then, the range will be 40-2=38 which is less than 40.
• As the greatest element will never be greater than 40 so we can say that range is always less than 40.
- o So, the answer to the question will be: Yes, the range of above given 6 numbers is always less than 40.
Hence, the above question ends here, and we found the maximum possible value of range for a, 13, 2, 9, b, 17 by using both the statements.
But, can we find the minimum value of the range in the above example using both the statements?
- • Yes, we can but how should we find the minimum possible value of the range?
- o If the value of a and b does not exceed the maximum number already present in the set i.e. 17, then there is no way the range of the set will increase.
- So, a, b has to be less than 17 for minimum range.
Let us now move to the next question.
e-GMAT Example 6
The set S has three different numbers a, b, and c such that a<b and b<c. Is the median of set S equal to the arithmetic mean of the three numbers?
- I. The sum of 3 numbers of set S is equal to 3 times one of the number.
II. Range of set S is equal to 2.
Solution
In this question, we are given:
- • 3 numbers: a, b, and c
• And we are asked to find if the median of a, b, and c is equal to the mean of a, b, and c.
- o Or, if b = a + b + c / 3?
o Or, 3b= a + b + c?
o Or, 2b= a + c?
Now, we will analyze each statement individually one by one.
Statement I. “The sum of 3 numbers of set S is equal to 3 times one of the number.”
- • Thus, we are given that “a + b + c” is thrice of either a or b or c.
• Hence, there are three possible cases:
- 1. a + b + c = 3a
- b + c = 2a………… (1)
Now, is equation (1) possible??
- • We know that a< b and b<c.
- o So, we can say that a<c and a<b
- So, both, b and c, are greater than a.
- No, right??
The sum of b and c will always be greater than 2a
Let us see another case.
- 2. a + b + c = 3b
- a + c = 2b ……… (2)
Now, is the equation (2) possible??
- • We know that a< b and b<c.
- o So, can the sum of two numbers be equal to 2b such that one number is less than b and another is more than b?
- It can be possible, right??
Think of 1,2, and 3.
• Hence, “a + b + c” can be equal to 3b.
Let us see the last case when a + b + c = 3c.
- 3. a + b + c = 3c
- a + b =2c…………. (3)
Now, is the equation (3) possible??
- • We already know that a < c and b < c.
- o So, and b both are less than c.
o So, can the sum of a and b be equal to 2c?
- No, right??
The sum of a and b will always be less than 2c.
Thus, the only possible case is a + b + c = 3b and hence, a + c = 2b.
Hence, we can answer the question with the help of statement 1 alone.
Statement II. “Range of set S is equal to 2”.
Now, I want to ask did you assume b=a+1 and c=a+2??
- • If your answer is yes:
- o Then, sadly you are incorrect. ☹
- o So, b can be any real number between a and c.
• However, c is equal to a+2 as c-a=2.
- o But, we cannot say if 2b = a + c or not.
Hence, we cannot answer the question with the help of statement 2 alone.
Thus, the correct answer is option (a).
Let us write all that we learnt from the above 3 examples related to range.
Key-Takeaways from the examples
- • In example 4, we learnt how to find the greatest and lowest value of a variable if the question is using the concept of Range.
- o To find the maximum value of the variable, we used the minimum element present in the set.
o And to find the minimum value of the variable, we used the maximum element present in the set.
• In example 5, we learnt how to find the maximum range and minimum value of a set of numbers when the value of 2 numbers of the set were not known to us.
- o To find the maximum range, we simply tried to maximize the value of the variable.
o And to find the minimum value of the variable, we simply tried to minimize the value of the variable.
And we also learnt not to assume anything that is not explicitly given in the question stem or not a valid inference.
With these learnings, we have come at the end of our article.
Key-Takeaways from the article:
- • In median, we learnt to find the minimum and maximum value of a variable present in a set of numbers by the application of median.
- o To find the maximum value of a variable, we minimize the value of all the other unknown variables present in set.
o To find the minimum value of a variable, we maximize the value of all the other unknown variables present in set.
• In Range, we learnt to find the greatest and lowest value of a variable present in a set of numbers by the application of range.
- o To find the maximum value of the variable, we use the minimum element present in the set.
o And to find the minimum value of the variable, we use the maximum element present in the set.
• We also saw the importance of careful reading and how wrong assumption can lead to wrong answer.
Now, to imbibe all the learnings, solve all the practice questions. The link of practice questions you can find in the first comment.
To read the 1st article of statistics: Solve any Mean and Standard deviation question under a minute !!!!
Read More such articles: Must Read Articles and Practice Questions to score Q51 !!!!
To reach Q51, solve one GMAT 700 level weekly from our "Question of the week” series.
Attachments
![]() Solve Median and Range questions in a minute.pdf [667.37 KiB]
Solve Median and Range questions in a minute.pdf [667.37 KiB]
Downloaded 392 times
Originally posted by EgmatQuantExpert on 11 Jul 2018, 07:51.
Last edited by EgmatQuantExpert on 13 Aug 2018, 00:37, edited 1 time in total.
Last edited by EgmatQuantExpert on 13 Aug 2018, 00:37, edited 1 time in total.
Kudos
Bookmarks
Hey Everyone,
Here is a list of questions specifically designed to help you apply the learnings from this article.
Exercise Questions
Question 1
Question 2
Question 3
Question 4
Detailed solutions will be posted soon.
Happy Learning!
Kudos
Bookmarks
Hey everyone,
We have added the pdf of the article.
Happy learning,
Regards,
Ashutosh
Quant Expert
e-GMAT
We have added the pdf of the article.
Happy learning,
Regards,
Ashutosh
Quant Expert
e-GMAT