Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 23 May 2018, 04:18.
Last edited by EgmatQuantExpert on 07 Aug 2018, 06:11, edited 6 times in total.
Last edited by EgmatQuantExpert on 07 Aug 2018, 06:11, edited 6 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
Objective of the article
Why you should read this article?
What will you learn from this article?
In this article, you will learn:
Solving Time and Work Problem: Conventional Method
In time and work problem, where people with different constant efficiencies do a certain work, we assume the total work to be constant. Mostly we solve these questions assuming the total work to be 1 unit. Let’s look at the following example:
e-GMAT Example 1
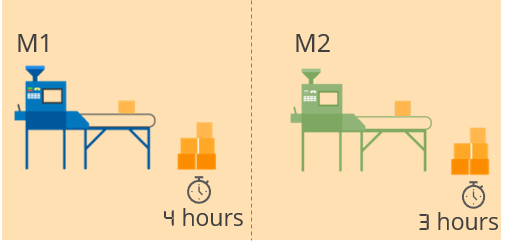
It would take one machine 4 hours to complete a large production order and another machine 3 hours to complete the same order. How many hours would it take both machines, working simultaneously at their respective constant rates, to complete the order?
Solution 1A: Conventional Method
Here it is given that two machines, working independently with their different constant efficiency, complete a large production order in 4 hours and 3 hours respectively.
Hence, working together, both the machines will take \(\frac{12}{7}\) hours to complete the production order.
Important observation
In the beginning of the solution, we have assumed the total constant work to be 1 unit.
Again, if you look carefully, the 1-day work of a person or a machine is calculated as the ratio of total work and the time taken.
Let us try to solve the same question using the method that we just mentioned.
Solution 1B: Changing the total work value
Let us assume the total work of production order is 12 units. Therefore, we can say:
Important Takeaway
If we compare the methods explained above, fundamentally they are same, with some difference in value-wise derivation. But the most important thing to observe is that there are no fractional intermediate calculations involved in the second solution.
Let us take another example to validate this learning:
e-GMAT Example 2
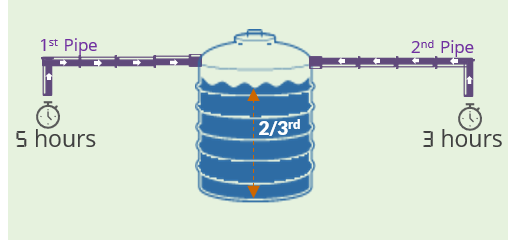
One inlet pipe fills an empty tank in 5 hours. A second inlet pipe fills the same tank in 3 hours. If both pipes are used together, how long will it take to fill 2/3rd of the tank?
Solution 2A: Conventional Method
In this question, it is given that one inlet pipe can fill an empty tank in 5 hours. A second inlet pipe fills the same tank in 3 hours.
As the capacity of the tank remains same, let’s assume the capacity of the tank is 1 unit.
Hence, to fill \(\frac{2}{3}\)rd of the tank, they will take = \(\frac{2}{3}/\frac{8}{15}\) hrs = \(\frac{2}{3} * \frac{15}{8}\) hrs = \(\frac{5}{4}\) hrs
Now, let’s try solving the same question using the LCM method:
Solution 2B: LCM Method
As the capacity of the tank remains same, let’s assume the capacity of the tank is 15 units.
[notice that 15 = LCM (3,5)]
Hence, to fill \(\frac{2}{3}\)rd of the tank, they will take = \(\frac{10}{8}\) hrs = \(\frac{5}{4}\) hrs
Important Takeaway
As you can see, both the problems can be solved using conventional method as well as LCM method. However, application of LCM method significantly decreases the calculation related, and therefore the time taken to solve a particular question becomes less.
Let us solve couple of more examples using the LCM method to reinforce our learning.
e-GMAT Example 2
Solving Time and Work Problem: LCM Method
In the following questions, we will solve the problems by applying LCM method only.
e-GMAT Example 3
Machines A and B always operate independently and at their respective constant rates. When working alone, Machine A can fill a production lot in 3 hours, and Machine B can fill the same lot in x hours. If A and B worked alternatively, while each work for 1 hour at a time, the total work gets completed in 4 hours. What is the value of x?
Solution 3
In this question it is given that machine A can fill a production lot in 3 hours, and machine B can fill the same production lot in x hours, when they are working alone.
However, they will take 4 hours to complete the job, when they are working alternatively for 1 hour each.
Let us assume the total work to be 3x units (LCM of 3 and x)
Important Takeaway
Unlike the previous questions, in this question we have a variable defined as x. Even in such case, we can apply the LCM method, as we did in the solved example, to get quick and accurate answer.
e-GMAT Example 4
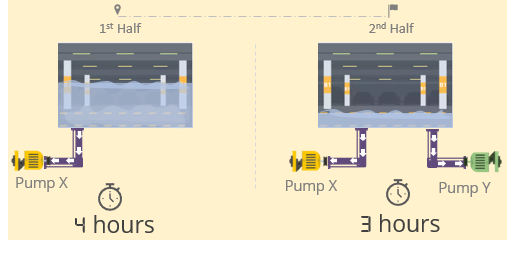
Working at a constant rate, pump X pumped out half of the water in a flooded basement in 4 hours. Then pump Y was started and the two pumps, working independently at their respective constant rates, pumped out the rest of the water in 3 hours. How many hours would it have taken pump Y, operating alone at its own constant rate, to pump out all of the water that was pumped out of the basement?
Solution 4
In this question there are two pumps working separately at their own constant rate.
As pump Y can clear 1 unit of water in 1 hour, it will take \(\frac{24}{1}\) hours = 24 hours to clear the whole amount of water, when working alone at its constant rate.
Important Observation
Apart from the usual application of the LCM method, another distinct observation we can do from this question, which is applicable in the previous question also. Let us see that:
Application of Efficiency in Time and Work problems
As we know, efficiency essentially means the rate of work, i.e. the amount of work done in unit time.
In a given scenario, efficiency can be used to explain the work rate either of an individual or of a group consists of similar objects. For a group, it is generally assumed that everyone within that group has the same efficiency.
Let us take an example of a time and work problem, which relates to the concept of efficiency:
e-GMAT Example 5
At a loading dock, each worker on the night crew loaded 3/4 as many boxes as each worker on the day crew. If the night crew has 4/5 as many workers as the day crew, what fraction of all the boxes loaded by the two crews did the day crew load?
Solution 5
In this question we have two separate groups of people to consider.
Let us look at the problem in detail.
It is given that there are two groups of workers – one operates at day time and the other one operates at night time.
We can show the whole data in the following table:
As we can see, total boxes loaded by day crew are 20 and by night crew are 12.
Hence, the boxes loaded by day crew as the fraction of all the boxes loaded by both the crew = \(\frac{20}{(20+12)} = \frac{20}{32} = \frac{5}{8}\)
Let us take one last example to demonstrate the application of efficiency:
e-GMAT Example 6
Machines X and Y work at their respective constant rates. How many more hours does it take machine Y, working alone, to fill a production order of a certain size than it takes machine X, working alone?
Option choices:
A) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are NOT sufficient.
Solution 6
In this question, two machines X and Y, with different efficiency, can work on a certain job.
Analysing Statement 1:
Hence, statement 1 is not sufficient to answer the question.
Analysing Statement 2:
Hence, statement 2 is not sufficient to answer the question.
Combining Both Statements:
As information from both the statements are required to solve the question, we can say the correct answer choice is Option C.
Takeaway from this article
What next in this series of article??
Next week we will come up with one more article in the Distance series.
In that article, we are going to discuss 3 common errors students make while solving Time and Work problems
Did you enjoy this article??
If you have enjoyed the article, then try the practice questions given below.
Solve Time and Work Problems Efficiently using Efficiency Method!
Objective of the article
Why you should read this article?
- • Are you someone who takes a long time to solve Time and Work?
• Do you get stuck in the fractional and decimal calculation related to Time and Work problems?
• Do you face problem in understanding how positive and negative efficiency works in Time and Work problems?
What will you learn from this article?
In this article, you will learn:
- • The application of LCM to solve Time and Work questions easily.
• A comparative study of methods of solving Time and Work problems – by using fraction and by using LCM method, which one should be used and when?
• How efficiency is defined and in what ways it can be implemented in problem solving
Solving Time and Work Problem: Conventional Method
In time and work problem, where people with different constant efficiencies do a certain work, we assume the total work to be constant. Mostly we solve these questions assuming the total work to be 1 unit. Let’s look at the following example:
e-GMAT Example 1
It would take one machine 4 hours to complete a large production order and another machine 3 hours to complete the same order. How many hours would it take both machines, working simultaneously at their respective constant rates, to complete the order?
Solution 1A: Conventional Method
Here it is given that two machines, working independently with their different constant efficiency, complete a large production order in 4 hours and 3 hours respectively.
- • As the total work done by both the machines are same, the work is constant here.
- • 1st machine in 4 hours can compete 1 unit of work
- • Hence, 1st machine in 1 hour can complete \(\frac{1}{4}\) units of work
- • Hence, 2nd machine in 1 hour can complete \(\frac{1}{3}\) units of work
• As the machines can complete \(\frac{7}{12}\) units of work in 1 hour time, to complete the whole work of 1 unit, they will take = \(\frac{1}{(7/12)}\) hours = \(\frac{12}{7}\) hours
Hence, working together, both the machines will take \(\frac{12}{7}\) hours to complete the production order.
Important observation
In the beginning of the solution, we have assumed the total constant work to be 1 unit.
- • Important thing one can observe here is that assuming the total work to be 1 unit or x units can make life difficult for us – because, when we calculate the 1-day work of that person or machine, chances are very high that we will be getting fractional values.
Again, if you look carefully, the 1-day work of a person or a machine is calculated as the ratio of total work and the time taken.
- • Therefore, if the assumed value of the total work is a multiple of the time taken, then the 1-day work will certainly be an integer value.
- • So, when we are assuming a value for the total work, we need to consider such a value which should be a multiple of the time taken by the different parties working on that job.
- • In other words, the assumed value of the total work can be taken as the least common multiple (LCM) of the given individual time taken by the persons or machines working on that job.
Let us try to solve the same question using the method that we just mentioned.
Solution 1B: Changing the total work value
Let us assume the total work of production order is 12 units. Therefore, we can say:
- • In 4 hours 1st machine can complete 12 units of work
- • Hence, in 1 hour 1st machine can complete 3 units of work
- • Hence, in 1 hour 2nd machine can complete 4 units of work
• As the complete work is 12 units, to complete the order they need to do total 12 units of work together
• Combined together, the machines are completing 7 units of work in 1 hour
- • Therefore, the machines will complete 12 units of work together in \(\frac{12}{7}\) hours
Important Takeaway
If we compare the methods explained above, fundamentally they are same, with some difference in value-wise derivation. But the most important thing to observe is that there are no fractional intermediate calculations involved in the second solution.
- • As the total work is assumed to be the LCM of 3 and 4, we are avoiding the fractional calculation, and thus, saving the overall calculation time.
Let us take another example to validate this learning:
e-GMAT Example 2
One inlet pipe fills an empty tank in 5 hours. A second inlet pipe fills the same tank in 3 hours. If both pipes are used together, how long will it take to fill 2/3rd of the tank?
Solution 2A: Conventional Method
In this question, it is given that one inlet pipe can fill an empty tank in 5 hours. A second inlet pipe fills the same tank in 3 hours.
As the capacity of the tank remains same, let’s assume the capacity of the tank is 1 unit.
- • As the 1st pipe takes 5 hours to fill 1 unit,
- • In 1 hour it will fill \(\frac{1}{5}\) units
- • Hence, in 1 hour it will fill \(\frac{1}{3}\) units
Hence, to fill \(\frac{2}{3}\)rd of the tank, they will take = \(\frac{2}{3}/\frac{8}{15}\) hrs = \(\frac{2}{3} * \frac{15}{8}\) hrs = \(\frac{5}{4}\) hrs
Now, let’s try solving the same question using the LCM method:
Solution 2B: LCM Method
As the capacity of the tank remains same, let’s assume the capacity of the tank is 15 units.
[notice that 15 = LCM (3,5)]
- • As the 1st pipe takes 5 hours to fill 15 units,
- • In 1 hour it will fill 3 units
- • Hence, in 1 hour it will fill 5 units
• The total work to be completed = (\(\frac{2}{3} * 15\)) = 10 units
Hence, to fill \(\frac{2}{3}\)rd of the tank, they will take = \(\frac{10}{8}\) hrs = \(\frac{5}{4}\) hrs
Important Takeaway
As you can see, both the problems can be solved using conventional method as well as LCM method. However, application of LCM method significantly decreases the calculation related, and therefore the time taken to solve a particular question becomes less.
Let us solve couple of more examples using the LCM method to reinforce our learning.
e-GMAT Example 2
Solving Time and Work Problem: LCM Method
In the following questions, we will solve the problems by applying LCM method only.
e-GMAT Example 3
Machines A and B always operate independently and at their respective constant rates. When working alone, Machine A can fill a production lot in 3 hours, and Machine B can fill the same lot in x hours. If A and B worked alternatively, while each work for 1 hour at a time, the total work gets completed in 4 hours. What is the value of x?
Solution 3
In this question it is given that machine A can fill a production lot in 3 hours, and machine B can fill the same production lot in x hours, when they are working alone.
However, they will take 4 hours to complete the job, when they are working alternatively for 1 hour each.
Let us assume the total work to be 3x units (LCM of 3 and x)
- • As machine A takes 3 hours to fill 3x units,
- • In 1 hour it will fill \(\frac{3x}{3}\) units = x units
- • Hence, in 1 hour it will fill \(\frac{3x}{x}\) units = 3 units
- • Therefore, in 2 hours’ time they will fill = (x + 3) units
• Hence, in 1 hour the production lot they fill = \(\frac{1}{2} * (x + 3)\) units
- • Units filled by A + units filled by B = total production units
Or, \(4 * \frac{1}{2} * (x + 3)\) = 3x
Or, 2x + 6 = 3x
Or, x = 6 hours
Important Takeaway
Unlike the previous questions, in this question we have a variable defined as x. Even in such case, we can apply the LCM method, as we did in the solved example, to get quick and accurate answer.
e-GMAT Example 4
Working at a constant rate, pump X pumped out half of the water in a flooded basement in 4 hours. Then pump Y was started and the two pumps, working independently at their respective constant rates, pumped out the rest of the water in 3 hours. How many hours would it have taken pump Y, operating alone at its own constant rate, to pump out all of the water that was pumped out of the basement?
Solution 4
In this question there are two pumps working separately at their own constant rate.
- • Pump X cleared half of the water present in the flooded basement in 4 hours
- • Therefore, to clear all the water, pump A would have taken twice the amount of time, i.e. 8 hours
- • As they took 3 hours to clear half the total amount of water, they would have taken double of that time, i.e. 6 hours, to clear the whole water
- • Pump X takes 8 hours to clear the whole water
• Pump X and Y together take 6 hours to clear the whole water
- • In 8 hours, pump X clears 24 units,
- • Hence, in 1 hour, pump X clears \(\frac{24}{8}\) units = 3 units
- • Hence, in 1 hour, pump X and Y together clear \(\frac{24}{6}\) units = 4 units
- • Therefore, amount of water cleared by Y in 1 hour = (4 – 3) unit = 1 unit
As pump Y can clear 1 unit of water in 1 hour, it will take \(\frac{24}{1}\) hours = 24 hours to clear the whole amount of water, when working alone at its constant rate.
Important Observation
Apart from the usual application of the LCM method, another distinct observation we can do from this question, which is applicable in the previous question also. Let us see that:
- • X can complete the whole work alone in 8 hours
• Y can complete the whole work alone in 24 hours
• X and Y together can complete the whole work in 6 hours
Application of Efficiency in Time and Work problems
As we know, efficiency essentially means the rate of work, i.e. the amount of work done in unit time.
- • The more time one takes to complete a job, the less efficient the person is.
• Similarly, the less time one takes to complete a job, the more efficient the person is.
In a given scenario, efficiency can be used to explain the work rate either of an individual or of a group consists of similar objects. For a group, it is generally assumed that everyone within that group has the same efficiency.
Let us take an example of a time and work problem, which relates to the concept of efficiency:
e-GMAT Example 5
At a loading dock, each worker on the night crew loaded 3/4 as many boxes as each worker on the day crew. If the night crew has 4/5 as many workers as the day crew, what fraction of all the boxes loaded by the two crews did the day crew load?
Solution 5
In this question we have two separate groups of people to consider.
- • Each member within the group has the same efficiency as other members
• However, group wise the efficiencies are different from each other
- • This means that everyone in the night crew has the same efficiency and everyone in the day crew has the same efficiency. However, the efficiency of day and night crew in this case is different.
Let us look at the problem in detail.
It is given that there are two groups of workers – one operates at day time and the other one operates at night time.
- • Each worker on the night crew loaded \(\frac{3}{4}\) as many boxes as each worker on the day crew
- • This statement defines the difference in efficiency of each worker belongs to night crew and day crew
• If we assume that each worker in the day crew loaded 4 boxes, then each worker in the night crew must have loaded \(4 * \frac{3}{4}\) boxes = 3 boxes
- • If we assume that there are 5 workers in the day crew, then there will be \(5 * \frac{4}{5}\) = 4 workers in the night crew
We can show the whole data in the following table:
As we can see, total boxes loaded by day crew are 20 and by night crew are 12.
Hence, the boxes loaded by day crew as the fraction of all the boxes loaded by both the crew = \(\frac{20}{(20+12)} = \frac{20}{32} = \frac{5}{8}\)
Let us take one last example to demonstrate the application of efficiency:
e-GMAT Example 6
Machines X and Y work at their respective constant rates. How many more hours does it take machine Y, working alone, to fill a production order of a certain size than it takes machine X, working alone?
- A. Machines X and Y, working together, fill a production order of this size in two-thirds the time that machine X, working alone, does.
B. Machine Y, working alone, fills a production order of twice the size in 6 hrs.
Option choices:
A) Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
B) Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are NOT sufficient.
Solution 6
In this question, two machines X and Y, with different efficiency, can work on a certain job.
- • The question asks the number of extra hours that machine Y takes to complete the job when working alone, compared to the time taken by machine X to complete the same job, working alone.
Analysing Statement 1:
- • As per the information given in statement 1, machines X and Y, working together, fill a production order of the same size in two-thirds the time that machine X, working alone, does.
• If we assume that machine X, working alone, takes t hours to complete the job, then from statement 1 we can say
- • Machine X and Y, working together, complete the whole work in \(\frac{2}{3}\)t hours
• Therefore, in that \(\frac{2}{3}\)t hours, machine Y completes \(\frac{1}{3}\)rd of the total work.
- • Hence, machine Y can complete the total work in \(\frac{2}{3}\)t * 3 hours = 2t hours
Hence, statement 1 is not sufficient to answer the question.
Analysing Statement 2:
- • As per the information given in statement 2, machine Y, working alone, fills a production order of twice the size in 6 hrs
• Hence, if we consider a production order of the original volume, machine Y will take 3 hours to complete it
• But from this statement, we cannot figure out any information regarding the work rate or time taken by X to complete the work
Hence, statement 2 is not sufficient to answer the question.
Combining Both Statements:
- • If we consider both statements together, we can say machine Y takes 2t hours to complete the whole job, which is equal to 3 hours
- • Hence, the value of t = \(\frac{3}{2}\) hours
- • As we already know t is equal to \(\frac{3}{2}\) hours, we can say machine X takes \(\frac{3}{2}\) hours to complete the job working alone
As information from both the statements are required to solve the question, we can say the correct answer choice is Option C.
Takeaway from this article
- • In Time and Work problems where we are supposed to assume the value of total work, it is always a good practice to assume the total work as the LCM of the given days (or any multiple of LCM), rather than assuming the total work as 1 unit – as it decreases the complex calculations involve with fractions.
• LCM method can still be applied when one of the data points are given in terms of variable
• Efficiency is inversely proportional to time taken.
• When working in groups, all are considered to be equally efficient within a group, whereas people have different efficiencies across groups.
What next in this series of article??
Next week we will come up with one more article in the Distance series.
In that article, we are going to discuss 3 common errors students make while solving Time and Work problems
Did you enjoy this article??
If you have enjoyed the article, then try the practice questions given below.
Attachments
![]() Time and work.pdf [599.89 KiB]
Time and work.pdf [599.89 KiB]
Downloaded 632 times
Originally posted by EgmatQuantExpert on 23 May 2018, 04:20.
Last edited by EgmatQuantExpert on 13 Aug 2018, 05:25, edited 1 time in total.
Last edited by EgmatQuantExpert on 13 Aug 2018, 05:25, edited 1 time in total.
Kudos
Bookmarks
Hey Everyone,
Here is a list of questions specifically designed to help you apply the learnings from this article.
Exercise Questions
Question 1
Question 2
Question 3
Question 4
Detailed solutions will be posted soon.
Happy Learning!
Kudos
Bookmarks
Hey everyone,
The official answers to all the practice questions have been posted.
Regards,
Tamal
e-GMAT
The official answers to all the practice questions have been posted.
Regards,
Tamal
e-GMAT