|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Kudos
Bookmarks
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
(N/A)
Question Stats:
66% (02:18) correct 33% (00:57) wrong
33% (00:57) wrong  based on 3 sessions
based on 3 sessions
History
Date
Time
Result
Not Attempted Yet
The cube above has volume equal to 64 cubic feet. If Points M and N are the midpoints of two edges of the cube, what is length MN, in feet?
A. \(4\sqrt{3}\)
B. \(3\sqrt{6}\)
C. \(4\sqrt{6}\)
D. \(6\sqrt{2}\)
E. \(2\sqrt{6}\)
Attachment:
GMAT-Club-Forum-g3rr7ebb.png [ 12.41 KiB | Viewed 142 times ]
Kudos
Bookmarks
Official Explanation
If s is the side length of a cube, then the cube’s volume = \(s^3\). Here, \(64 = s^3,\) so \(s = 4,\). Then AB = 4, and MA = NB = 2 in the figure below, because M and N are midpoints of two of the edges.

Now draw MB and form the two right triangles, MAB and MBN.
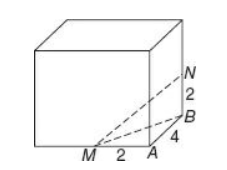
MB is the hypotenuse of a right triangle with legs equal to 2 and 4, so
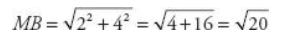
by the Pythagorean Theorem. This length becomes a leg in the second right triangle MBN.
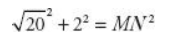
Therefore,

Answer: E

GMAT-Club-Forum-pcayy9do.png [ 9.54 KiB | Viewed 104 times ]

GMAT-Club-Forum-qlkecpct.png [ 11.33 KiB | Viewed 104 times ]
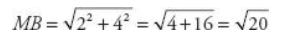
GMAT-Club-Forum-ajb0953u.png [ 6.8 KiB | Viewed 106 times ]
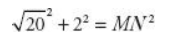
GMAT-Club-Forum-vrvpczp1.png [ 4.52 KiB | Viewed 106 times ]

GMAT-Club-Forum-rk501dgi.png [ 5.98 KiB | Viewed 104 times ]
If s is the side length of a cube, then the cube’s volume = \(s^3\). Here, \(64 = s^3,\) so \(s = 4,\). Then AB = 4, and MA = NB = 2 in the figure below, because M and N are midpoints of two of the edges.
Now draw MB and form the two right triangles, MAB and MBN.
MB is the hypotenuse of a right triangle with legs equal to 2 and 4, so
by the Pythagorean Theorem. This length becomes a leg in the second right triangle MBN.
Therefore,
Answer: E
Attachment:
GMAT-Club-Forum-pcayy9do.png [ 9.54 KiB | Viewed 104 times ]
Attachment:
GMAT-Club-Forum-qlkecpct.png [ 11.33 KiB | Viewed 104 times ]
Attachment:
GMAT-Club-Forum-ajb0953u.png [ 6.8 KiB | Viewed 106 times ]
Attachment:
GMAT-Club-Forum-vrvpczp1.png [ 4.52 KiB | Viewed 106 times ]
Attachment:
GMAT-Club-Forum-rk501dgi.png [ 5.98 KiB | Viewed 104 times ]








