|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Kudos
Bookmarks
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
(N/A)
Question Stats:
100% (01:05) correct 0% (00:00) wrong
0% (00:00) wrong  based on 2 sessions
based on 2 sessions
History
Date
Time
Result
Not Attempted Yet
The height, h, of a thrown ball as a function of t, the amount of time it has been in the air, is given by h(t) = –10t^2 + 40t. What is the maximum height attained by the ball?
A. 22
B. 0
C. 40
D. 80
E. 160
A. 22
B. 0
C. 40
D. 80
E. 160
Originally posted by Sajjad1994 on 02 Nov 2025, 09:54.
Last edited by Sajjad1994 on 02 Nov 2025, 10:01, edited 1 time in total.
Last edited by Sajjad1994 on 02 Nov 2025, 10:01, edited 1 time in total.
Kudos
Bookmarks
Official Explanation
Factor out the common factor, \(–10t,\) to obtain \(h(t) = –10 t(t – 4)\). Find the t-intercepts (x-axis intercepts) of the graph by setting \(y = h(t) = 0.\) Then \(0 = –10 t(t – 4).\) The product is 0 when either factor is 0, so \(–10t = 0\) or \(t – 4 = 0,\) and \(t = 0\) or \(t = 4.\) By the symmetry of a parabola, the vertex will lie on the vertical line t = 2, because 2 is halfway between the t-intercepts of 0 and 4. The maximum height of the ball will be the y-coordinate of the vertex, namely h(2), which is by definition the height of the ball at time 2. h(2) = –10 × 22 + 40 × 2 = –40 + 80 = 40, (C).
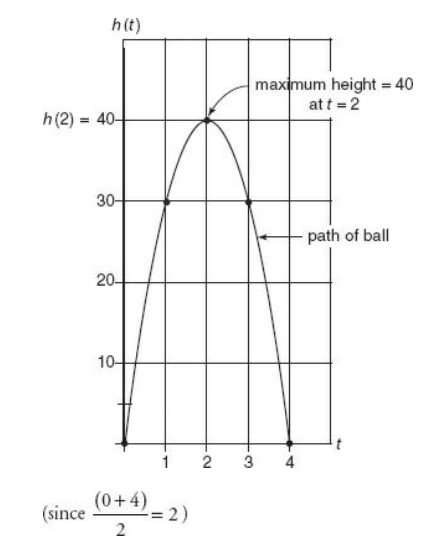
Answer: C

GMAT-Club-Forum-lmf35baz.png [ 55.77 KiB | Viewed 64 times ]
Factor out the common factor, \(–10t,\) to obtain \(h(t) = –10 t(t – 4)\). Find the t-intercepts (x-axis intercepts) of the graph by setting \(y = h(t) = 0.\) Then \(0 = –10 t(t – 4).\) The product is 0 when either factor is 0, so \(–10t = 0\) or \(t – 4 = 0,\) and \(t = 0\) or \(t = 4.\) By the symmetry of a parabola, the vertex will lie on the vertical line t = 2, because 2 is halfway between the t-intercepts of 0 and 4. The maximum height of the ball will be the y-coordinate of the vertex, namely h(2), which is by definition the height of the ball at time 2. h(2) = –10 × 22 + 40 × 2 = –40 + 80 = 40, (C).
Answer: C
Attachment:
GMAT-Club-Forum-lmf35baz.png [ 55.77 KiB | Viewed 64 times ]








