Bunuel wrote:
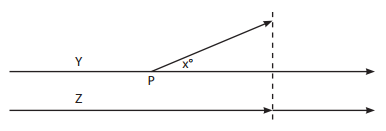
Cars Y and Z travel side-by-side at the same rate of speed along parallel roads as shown above. When car Y reaches point P, it forks to the left at angle x°, changes speed, and continues to stay even with car Z as shown by the dotted line. The speed of car Y beyond point P is what percent of the speed of car Z?
(1) The speed of car Z is 50 miles per hour.
(2) x = 45
Kudos for a correct solution.Attachment:
2015-10-08_1848.png
Type of question: What Is the Value? The question asks for “the speed of car y (beyond point p) as a percent of the speed of car z.” Note: This is the same as asking for Distance/Time of car y as a percent of the Distance/Time of car z.
Given information in the question stem or diagram: The roads that car y and z are traveling on are parallel until point P. At point P the cars are even and then car y makes a turn of x degrees and continues to keep up with car z. The key information that you need to leverage from this given information is that the times will be the same for each car.
Statement 1: “The speed of car z = 50 mph.” This statement does not give any information about the speed of car y, nor about the extra distance that car y must travel. This statement is not sufficient on its own. Eliminate choices A and D, and note that this is a classic “Why Are You Here?” set-up. This statement is clearly insufficient on its own so you will want to consider whether it is important in relation to Statement 2.
Statement 2: “The measure of angle x = 45 degrees.” This statement may not appear sufficient until you realize that you do not actually need to know the speeds of cars y and z. Because the cars are keeping up with each other, the time that each car travels must be equal. That means that the increased percentage of distance that car y has traveled will be the same as the increased percentage of the rate of car y compared to car z. In other words, determining the ratio of the distance of y to the distance of z is enough to answer this question because the times are necessarily the same. While you do not need to do it, the actual mathematical solution is below. Also, note that this is a classic example of the “Why Are You Here?—Temptation” set-up that is used so often on harder problems. They have tempted you with a statement (the speed of car z) that is not necessary to determine sufficiency. Statement 2 is sufficient by itself.
The road that car y travels on after point P forms a triangle with the road that y was traveling on (that road is parallel to the road z is traveling on). This triangle is a right triangle with the right angle formed by the dotted line. Statement 2 gives the measure of x at 45 degrees. That means you have a 45–45–90 triangle with the distance that y has traveled as the hypotenuse and the distance z has traveled as one of the shorter sides. The hypotenuse is √2 bigger than the shorter sides, so car y is √2 faster than car z. As noted above, this is sufficient and
the correct answer is B.
_________________



 55%
(hard)
55%
(hard)
 38%
(01:58)
wrong
38%
(01:58)
wrong  based on 1910
sessions
based on 1910
sessions





