Zap the Weighted Average Brutes
BY KARISHMA, VERITAS PREP
I visit the GMAT Club forum regularly and discuss some ideas, some methodologies there. The weighted averages method I discussed in my previous two posts is one of my most highly appreciated inputs on the forum. People love how easily they can solve some of the most difficult questions by just drawing a scale or using a ratio. If you are not a Quant jock, I am sure you feel a chill run down your spine every time you see a mixtures problem. But guess what, they are really simple if you just use the same weighted average concepts we discussed in the previous two posts. Let’s look at a mixtures question in detail:
Question: Mixture A is 20 percent alcohol, and mixture B is 50 percent alcohol. If the two are poured together to create a 15 gallon mixture that contains 30 percent alcohol, approximately how many gallons of mixture A are in the mixture?(A) 3 gallons
(B) 4 gallons
(C) 5 gallons
(D) 10 gallons
(E) 12 gallons
Solution:Let’s try and imagine what is taking place here:

Imagine two tumblers, one containing Mixture A and the other containing Mixture B. The mixtures from the two tumblers are poured into a new big empty tumbler. The first thing that we can conclude from this step is that V1 + V2 gallons = 15 gallons because the total volume when you combined the mixtures turned out to be 15 gallons (in the big tumbler).
Can you say anything about the relative value of V1 and V2? Can you say which one will be greater? We discussed in the previous post that when we find the weighted average of two quantities, the average is closer to the one which has higher weight because that quantity ‘pulls’ the average toward itself. So if the new mixture contains 30% alcohol, which of the two mixtures – A (20% alcohol) or B (50% alcohol), will have higher volume? Obviously A because it pulled the average toward itself. The average, 30% alcohol, is closer to 20% than to 50%. Now, let’s calculate exactly how much of the 15 gallons was mixture A and how much was mixture B.
\(\frac{w_1}{w_2} = \frac{(A_2 – A_{avg})}{(A_{avg} – A1)}\)
\(\frac{w_1}{w_2}= \frac{(50 – 30)}{(30 – 20)} = \frac{2}{1}\)
Ratio of volume of mixture A : volume of mixture B = 2:1.
So out of a total of 15 gallons, 10 gallons will be mixture A and 5 gallons will be mixture B. (Check out the post on Ratios if you are not sure how we arrived at this.)
Let’s try the same thing using the scale method:
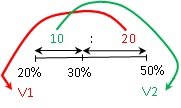
V1 : V2 = 2:1
So out of a total of 15 gallons, 10 gallons will be mixture A and 5 gallons will be mixture B. It wasn’t very bad, was it?
This question is discussed HERE.
And now, let’s try a quick example that looks ominous. People end up making tons of equations with ‘x’ and ‘y’ to solve this one but we can do it in a moment!
Question: There are 2 bars of copper-nickel alloy. One bar has 2 parts of copper to 5 parts of nickel. The other has 3 parts of copper to 5 parts of nickel. If both bars are melted together to get a 20 kg bar with the final copper to nickel ratio of 5:11. What was the weight of the first bar?(A) 1 kg
(B) 4 kg
(C) 6 kg
(D) 14 kg
(E) 16 kg
Solution:This question might look different from the question above but it is actually very similar to it. Focus on any one of the two elements, say Copper (or Nickel if you fancy it more. Either way, you will get the same answer). Forget about the other one. If you notice, in the question above there are two elements in each mixture too (obviously, that is why they are called mixtures!) – Alcohol and Water. 20% Alcohol means that the rest 80% is Water. We just work with the concentration of Alcohol because it is given explicitly to us. We could as well say that mixture A has 80% water and mixture B has 50% water and the combined mixture has 70% water. Still the ratio obtained will be 2:1. But, still, somehow, giving the ratio of both Copper and Nickel in this question throws people off.
Let me quote one of my favorite GMAT instructors here: “And this is one of many reasons why McDonald’s, the greatest marketing organization on earth, is a lot like the GMAT, the test that can help you get into the greatest marketing MBA programs on earth. They know how to make those tiny tweaks that make massive differences, at least in perception to the end consumer.” (Check out the complete(-ly) delicious article that discusses Shamrock Shakes here.)
Anyway, let’s get back to this question. I am keen to show you that it is, in fact, just like the previous question.
First bar is 2/7th copper (2 parts copper and 5 parts nickel to get a total of 7 parts). Second bar is 3/8th copper and the combined alloy is 5/16th copper.
Now, let’s calculate the ratio of weights of the two bars.
\(\frac{w_1}{w_2} = \frac{(A_2 – A_{avg})}{(A_{avg} – A_1)}\)
\(\frac{w_1}{w_2} = \frac{(\frac{3}{8} – \frac{5}{16})}{(\frac{5}{16} – \frac{2}{7})} = \frac{7}{3}\)
So weight of first bar: weight of second bar = 7:3
Out of a total of 20 kgs, the weight of the first bar was 14 kg and the weight of the second bar was 6 kg.
Or we can use the scale method too.
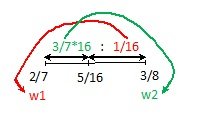
So the ratio of their weights is 1:3/7 or 7:3
Out of a total of 20 kgs, the weight of the first bar was 14 kg and the weight of the second bar was 6 kg.
This question is discussed HERE.
Hope these questions don’t look very intimidating now. Use this method for your mixture problems; they won’t feel like problems any more!
Attachment:
Ques3.jpg
Attachment:
Ques2.jpg
Attachment:
Ques42.jpg
Please explain the last part, I am getting first bar as 14kg and second bar as 6 kg. W1*(1/16)=w2*(











