Why is “Infer” a critical process skill to master GMAT Quant?

Why is “Infer” a critical process skill to master GMAT Quant?

THE DEFINITION


In our previous article, we learned this definition of the process skill of ‘infer’. We learned the following aspects about this skill.

1. To infer, we use information from these two sources:

o the information given in the question
o our conceptual knowledge

2. We need to continually draw inferences through the solution while solving

o In the beginning
o In the middle
o And in the end

3. If we consciously ‘infer’ information, we will chart out our path towards the solution of the question at hand.

As we solve a quant question, if we continuously draw inferences, our ability to solve that question increases. Thus, we must develop this process skill to draw inferences in order to maximize our quant score. Please click here if you would like to see a video on this skill

In this article, we will show you how this process skill needs to be applied on quant questions. To do the same, we have selected difficult questions from official sources covering topics as diverse as Number Properties, Algebra, and Geometry. At the end of this article, you can take a short quiz to test your ability set to draw inferences.

To maximize learning, follow the sequence of steps below for each example:

1. Solve the question on your own.
2. Review the detailed solution.
3. Identify where you faltered if you faltered.
4. Read the analysis of the process skill.
5. Make your notes.

Also, in each of the solutions, we have highlighted the following aspects

1. What did we infer?
2. What information did we use to draw the inference?
3. What question did we ask to draw the inference?

This will help you not only not only observe how we applied this process skill but also learn the framework for doing so while solving questions on your own.

So, let’s get started with our first example. This example is from Number Properties topic.

“INFER” IN NUMBER PROPERTIES QUESTIONS

First, solve this official question. It is from OG Advanced book.

The difference 942 − 249 is a positive multiple of 7. If a, b, and c are nonzero digits, how many 3-digit numbers abc are possible such that the difference abc − cba is a positive multiple of 7?

A. 142
B. 71
C. 99
D. 20
E. 18

Next, review the solution in this screenshot. If you would prefer a video solution, click here.


Next, observe the “infer” process skill at play

There are two points in the solution when we drew an inference to proceed. We will talk about each one by one.

1. What did we infer?

a. (a-c) is a multiple of 7.

2. What information did we use to infer?

i. Source 1 - from processing of question statement

a. 99 (a-c) is a multiple of 7
ii. Source 2 - Conceptual understanding

a. 99 is not a multiple of 7
b. Our understanding of products and multiple. For example:

• 2 x 25 is a multiple of 5 --> at least one of the two – 2 or 25 should be a multiple of 5 --> 2 is not a multiple of 5, 25 is.

3. What question did we ask to draw the inference?

a. If 99 (a-c) is a multiple of 7, then what can be inferred about a and c?

While solving quant questions, you should be actively engaged so that you can draw such inferences and move forward in your solution. This action requires that you pull pertinent information from your conceptual knowledge bank.


Now let’s talk about the second inference in this question:

1. What did we infer?

a. a - c = 7

2. What information did we use to infer?

a. Source 1 - from the first inference

i. a-c is a multiple of 7
b. Source 2 – from the constraint in the question statement

i. Both a and c are single digit numbers

3. What question did we ask to draw the inference?

a. If a and c are single digit numbers, and a-c is a multiple of 7, then what could be possible values of a – c?

i. a – c = 7.

As you read this analysis, you may notice that even though this is a 700-level question, there is no rocket science involved here. That is the beauty of the application of process skills. They simplify your job through the solution – they plow away the complexity and smoothen the surface as you move along through the solution.

Let’s now look at an Algebra question.

“INFER” IN ALGEBRA QUESTIONS

First, solve this official question. It is from OG Advanced book.
What is the value of x?

(1) \(x^4 + x^2 + 1 = \frac{1}{x^4 + x^2 + 1}\)
(2) \(x^3 + x^2 = 0\)

Next, review the solution in this screenshot. If you would prefer a video solution, click here.


Next, observe the “infer” process skill at play

1. What did we infer?

a. It is not possible that \(x^2(x^2+1) = -2\)

2. What information did we use to infer?

a. Source 1 - from processing of question statement

i. Two possible roots of the equation \((x^2(x^2+1)+ 1)^2 = 1\)


b. Source 2 - Conceptual understanding
i. Square of a number cannot be negative.
ii. Product of two non-negative numbers cannot be negative.

3. What question did we ask to draw the inference?

a. What could be the value of x if this equation is true?

Notice what would have happened if we had not drawn this inference. We would have thought that since there is a quadratic equation, we will get multiple roots and hence we will not be able to find a unique value of x and hence statement 1 is not sufficient. And as a result, we would have rejected choice A – the correct answer.

Such is the peril of not applying the “infer” process skill.


Let’s now look at the application of this core skill on a Geometry question.

“INFER” IN GEOMETRY QUESTIONS

First, solve this official question. It is from OG Advanced book.



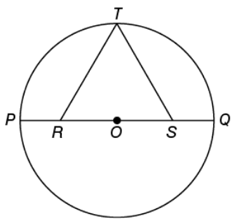
In the figure above, PQ is a diameter of circle O, PR = SQ, and ∆RST is equilateral. If the length of PQ is 2, what is the length of RT?

A. \(\frac{1}{2}\)
B. \(\frac{1}{√3}\)
C. \(\frac{√3}{2}\)
D. \(\frac{2}{√3}\)
E. √3

Next, review the solution in this screenshot. If you would prefer a video solution, click here.


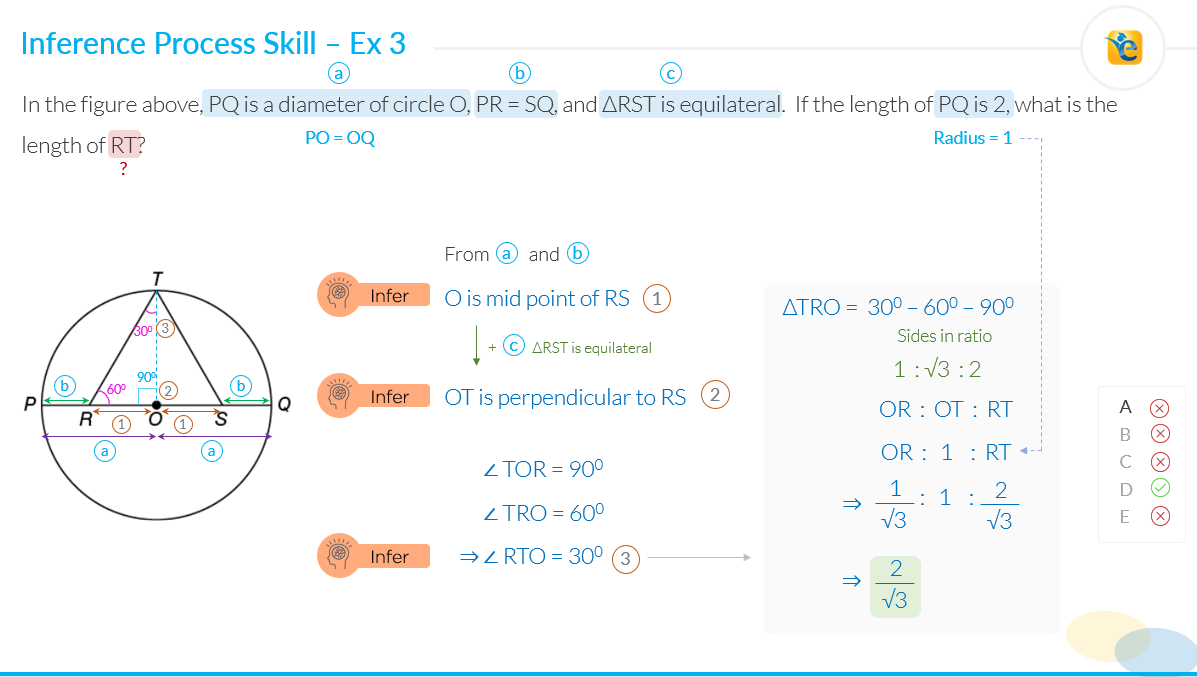
Next, observe the “infer” process skill at play

There are three points in the solution when we drew an inference to proceed. And failure to draw any of these inferences would have made the solution of this question very difficult. We will talk about each one by one.

1. What did we infer?

a. O is the midpoint of RS.

2. What information did we use to infer?

a. Source 1 – From the processing of the question statement.

• PQ is the diameter --> PO = OQ
b. Source 2 – From the question statement

• PR = SQ

3. What question did we ask to draw the inference?

• If PO = OQ and PR = SQ, can we deduce anything about OR and OS?

To infer that O is the midpoint of RS, we did not even need to use any of our specialized conceptual understanding. All we did was absorb the information and asked the next logical question – we are given information about the larger segments - PO and OQ and one of their parts – PR and SQ. So, what can we deduce about the other parts – OR and OS – especially since these parts fall in the triangle pertinent to what the question is asking us.

Applying the ‘infer’ process skill helps us take baby steps – we are drawing inferences about the next logical aspect and helps in breaking down a lengthy solution in small doable parts.


Now let’s talk about the second inference in this question:

1. What did we infer?

a. OT is perpendicular on RS.

2. What information did we use to infer?

a. Source 1 – from the 1st inference

• O is the midpoint of RS.
b. Source 2 – Information in the question statement

• ∆RST is equilateral
c. Source 3 – Conceptual understanding that in an equilateral triangle, the perpendicular on a side bisects that side.

3. What question did we ask to draw the inference?

• If we know that O is the midpoint of RS and ∆RST is equilateral, can we deduce anything else about the sides or angles in this triangle?

Before I move on to the third inference, I want you to notice the theme of these inferences – if you look at them in isolation, you will find them rather trivial – in fact you would say – this is so simple – it’s a no brainer. And that is exactly the point – in isolation, this analysis is indeed very simple. And that is indeed the magic of applying the ‘infer’ process skill. This process skill enables you to break a complicated question into small simple steps that lead you to the solution of the problem. And that is why it is so very important to master this process skill. And the key to mastering this skill is to constantly observe information and ask questions.


Now let’s talk about the third inference in this question:

1. What did we infer?

a. ∠RTO = 30° --> The triangle in question is a 30°- 60°-90° triangle.

2. What information did we use to infer?

a. Source 1 – from the 2nd inference

• OT is perpendicular on RS  ∠TOR = 90°
b. Source 2 – Conceptual understanding that sum of angles in a triangle = 180° and that all angles in an equilateral triangle = 60°

3. What question did we ask to draw the inference?

• Given the two angles as 30° and 60°, what do we know about the third angle?

Before you move on to the conclusion of this article, review the solution once again and notice the three inferences that we drew to solve the question.

CONCLUDING REMARKS

We saw three difficult 700-level questions from multiple sub-sections in quant.

Here is the list of concepts required to solve these questions:

1. Number representation – a 3-digit number abc = 100a + 10b + c
2. Basic understanding of product and multiples
3. Solving quadratic equation
4. Square of a number is non-negative
5. Sum of angles in an equilateral triangle
6. Side ratio of 30°-60°-90° triangle

And now I will rather abruptly conclude this article by leaving you with these questions.

• Do you have a solid understanding of the concepts listed above?
• If the concepts tested are rather straight forward, then how come the questions are this difficult?
• What makes the questions difficult – is it the conceptual understanding or is it something else?

Now I want you to look at the screenshots of the solutions in this article and then ask these questions:

• Do you stay this engaged while solving questions?
• If individually these inferences are so simple, then why do you falter to apply them while solving such difficult questions?
• What are you going to do to master ‘infer’ process skill?

Ok, I will not end the article that abruptly! I will answer the last question:

HOW CAN YOU DEVELOP THIS PROCESS SKILL?

Building a process skill takes little time if you put in the deliberate effort.

The first thing you need to do is to prepare from sources that give you such detailed solutions so that you can identify which inference you were not able to draw-

Second – make sure that whenever you make a mistake or take longer to solve a question, attribute it to lack of a concept, or a process skill, or a calculation mistake.

Lastly, every couple of days, revise the questions where you made a mistake. If you do this, you will discover that you make fewer mistakes, and your score improves as you practice.