Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 20
01:30 PM EST
-02:30 PM IST
Learn how Kamakshi achieved a GMAT 675 with an impressive 96th %ile in Data Insights. Discover the unique methods and exam strategies that helped her excel in DI along with other sections for a balanced and high score. - Nov 22
06:30 AM PST
-08:30 AM PST
Let’s dive deep into advanced CR to ace GMAT Focus! Join this webinar to unlock the secrets to conquering Boldface and Paradox questions with expert insights and strategies. Elevate your skills and boost your GMAT Verbal Score now! - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 24
07:00 PM PST
-08:00 PM PST
Full-length FE mock with insightful analytics, weakness diagnosis, and video explanations! - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 26 Apr 2018, 04:07.
Last edited by EgmatQuantExpert on 21 Aug 2019, 22:06, edited 7 times in total.
Last edited by EgmatQuantExpert on 21 Aug 2019, 22:06, edited 7 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
Why should you read this article?
Before embarking on reading the article, ask yourself a few questions:
If the answer to any of the above questions is yes, then we strongly recommend you to continue reading the article.
In this e-GMAT article you will learn a structured approach to solve probability questions.
We will also explain 3 most common mistakes that students make in probability question and the best way to solve such question.
Objective of the article
In the article, we will learn:
Now let us begin the article with a very frequently used concept of non-events in probability.
Non-event method
At times, we may come across a probability question, in which we need to find a lot of favorable cases, which is known as favorable events in probability jargon.
Now, finding all the cases is time consuming and might involve a lot of calculations. In such situations, we may end up making a mistake too.
Hmm...so how should we tackle such a situation? Obviously there has to be a better way to do it!
Well, the better way or better method is known as the - Non-Event Method, in which we find all the cases which we do not want (known as non-event) and subtract it from the favorable cases.
This method reduces a lot a calculation but at the same place, test your logical thinking skills.
Let’s understand what I am trying to say with the help of an example!
e-GMAT Example 1
Q--If x is to be chosen at random from the set {1,2,3,4} and y is to be chosen at random from the set {5,6,7}, what is the probability that x*y will be even?
Now, how should be we solve this question???
Solution
We know that Probability of occurring an event= \(\frac{Total\ number\ of\ ways\ in which\ the\ event\ can\ occur}{total\ outcomes}\)
Thus, we need two things:
Number of ways in which x *y is even
x*y can be even in three ways:
Thus, total ways= Ways in which both x and y are even+ Ways in which only x is even + Ways in which only y is even
Total outcomes:
Total outcomes= Ways in which x can be selected * Ways in which y can be selected
Thus, P (x*y is even) = \(\frac{8}{12}\)= \(\frac{2}{3}\)
Although this example was an easy one and we got 3 cases, what if first set has 8 numbers and second set had 9 numbers???
Then counting every possible case will be tedious!!
Let us now solve this question by another approach: Non-event method.
Non-event Method:
The multiplication of x and y can give only two possibilities:
Thus, if we add the probabilities of all the possible cases then their sum should be equal to 1.
Hence,
Thus, if we find P (when x*y is odd) then we just need to subtract its values from 1 to get the actual answer.
And, surprisingly the number of ways when x*y is odd is only 1- When x and y both are odd!!!
Thus, P (x*y is even) = 1- \(\frac{4}{12}\)=\(\frac{8}{12}\)
Oh!! This was easy!!!!
So, can you observe that you have to think a step ahead to visualize which method will be easy for you????
And yes, non-event method reduced our calculation too.
Thus, the learning from the above example is that whenever we see that there are lot of favorable events, we should always check if the non-events is less. And if that is the case, we should find the non-events first and then subtract it from the total cases.
Now, let’s come to come to the common type of errors that a student makes while solving the questions by non-event method.
Missing cases: Error Type 1
Let us take an interesting example. Try to solve the question first before moving to the solution. There is high possibility that you might end up making the mistake highlighted in the later part of the article.
e-GMAT Example 1
Q--In a box of 12 pens, total 3 are defective. If a customer buys 2 pens selected at random from the box., what is probability that neither pen will be defective?
Solve this question by non-event method only.
Solution
If your answer is \(\frac{21}{22}\) then you marked the wrong answer. ☹
Read further to understand how to avoid such mistakes!
Do you know that I knew how did you arrived at \(\frac{21}{22}\)??
If that is the case, then you made a very common error!!! You missed a few cases.
Let us see how to correctly apply non-event method in this question.
Correct approach:
Let us write all the possible cases in which customer can buy the two pens.
Since the sum of the probability of all the possible cases is 1, thus
Now, can you find P (neither pen is defective)?
Can you see the mistake you made when you solved using the formula P (neither pen will be defective) = 1- P (Both the pens are defective)????
• You missed one case. This is an error of Missing cases.
Now, we only have to calculate the values of P (None of the pen is defective) and P (1 defective pen and 1 non-defective pen) and we will have the answer.
But to arrive at the above equation of P (Both the pens are defective) you need to think logically, since GMAT tests your logical thinking skills.
Now, let us find P (Both the pens are defective) and P (1 defective pen and 1 non-defective pen).
P (Both the pens are defective):
P (1 defective pen and 1 non-defective pen):
Thus, P (neither pen is defective) = 1 - \(\frac{1}{22}\) - \(\frac{9}{22}\) = 1-\(\frac{10}{22}\)= \(\frac{12}{22}\)
Key Takeaways
When to consider the arrangement: Error Type-2
While solving any probability question, most of the students forget that for different arrangements of a particular case, the probability is also different.
They do not consider all the arrangements and calculate the probability of one of the possible cases which results into wrong answer.
Let us understand what I am trying to say with the help of an example.
e-GMAT Example 1
Q--There are 10 solid colored balls in a box including 1 green ball and 1 yellow ball. If 3 of the balls in the box are to be chosen at random without replacement, what is the probability that three balls chosen will include the green ball but not the yellow ball?
Solution
Now, have you started thinking of all the possible cases??
If not, do not worry!!! After reading this article and practicing questions, thinking of all the possible cases will be the next step you will be doing without even realizing. ?
P (Selecting 1 green but not the yellow ball) = \(\frac{P (Select\ 1\ green\ and\ select\ 2\ solid\ colored\ balls)}{Total\ outcomes}\)
Thus,
Thus, our answer is \(\frac{7}{90}\)???????
But most of the students mark \(\frac{7}{90}\) as the correct answer to this question.
Let us understand why this answer is not correct.
Can you find in how many ways we can choose 3 balls such that 1 ball is green, and 2 balls are solid colored???
Let us list down the possible orders.
Total cases=3
We can also think in this way that we have three balls- 1 Red and 2 Solid colored balls. In how many we can arrange them?
So, there are 3 arrangements possible, but we considered only 1 case i.e R S S and calculated its probability.
So how should we go about to find the answer????
So, let us look at another way!
Let us first find P(S R S) and P(S S R).
If you observe, then all the three cases have the same probability.
Thus, multiplying 3 with P(R S S) will give our final answer and 3 is the number of ways in which you can select 3 balls- 1 Red and 2 Solid colored balls.
Key takeaways from the example:
If we replace 3 by the number of ways balls can be arranged, then we can conclude:
e-GMAT Example 2
Q-- A box contains 100 balls, numbered from 1 to 100.If three balls are selected at random and with replacement from the box, what is the probability that the sum of the three numbers on the three balls selected will be odd?
Solution
Can you think of all the possible cases in which we can get the sum of three numbers to be odd?
There are 2 possible cases:
Probability when all the numbers are odd:
Probability when two numbers are even, and one is odd:
However, this case can occur in 3!/2!= 3 ways.
Hence,
Thus, total probability= \(\frac{1}{8}\)+\(\frac{3}{8}\)=\(\frac{4}{8}\)= \(\frac{1}{2}\)
Probability in dependent events:
Let us look at a slightly complex problem of probability and a question that is put so beautifully that most of the aspirants fall prey to the trap of this question and mark a wrong answer.
Do you want to test your knowledge of probability??? Let’s give it a try. ?
e-GMAT Example 1
Q--If the probability is 0.54 that stock A will increase in value during the next month and the probability is 0.68 that stock B will increase in value during the next month, what is the greatest value for the probability that neither of these two events will occur.
Solution
Is the answer equal to 0.1472 or 0.32????
If your answer is 0.1472 then this is the 3rd mistake you will avoid after reading this article. ?
Let us see why 0.1472 is wrong.
Can you observe that the language of this question is a little different???
We know how to find the probability but what is greatest probability?
Well, don’t worry!! This is a question of probability where two events are dependent.
Let us understand independent and dependent events first.
Independent Events
Dependent Events
And our question is a perfect example of dependent events.
So, how do we calculate the greatest probability such that neither of these two events occur????
Let us see two dependent events, A and B, pictorially.
Since P(A)= 0.54, P’(A)= 0.46
This is shown pictorially below (Fig 1):
Here, the full circle represents the total probability in which all the events can occur(A might increase and decrease) and the small circle inside it represents the probability of all the events in which A can decrease .
From the diagram, we know that we need to maximize the area/probability of P’(A).
So, how can we maximize this keeping in mind that A and B are dependent???
This is the way to solve questions of dependent probability.
So, we learnt 3 ways to avoid mistakes while solving probability questions. Let us summarise everything.
Key Takeaways from the article
3 deadly mistakes you must avoid in Probability
Why should you read this article?
Before embarking on reading the article, ask yourself a few questions:
- • Are you someone who doesn’t know how to solve a probability question?
• Are you confused which cases should be considered and which cases should be ignored while calculating the probability?
• Are you someone who is confused while considering all the cases of arrangement??
If the answer to any of the above questions is yes, then we strongly recommend you to continue reading the article.
In this e-GMAT article you will learn a structured approach to solve probability questions.
We will also explain 3 most common mistakes that students make in probability question and the best way to solve such question.
Objective of the article
In the article, we will learn:
- • How to solve a probability question by the non-event method.
• How to calculate the probability when more than 1 arrangement is possible.
• How to find the greatest or lowest value of the probability.
Now let us begin the article with a very frequently used concept of non-events in probability.
Non-event method
At times, we may come across a probability question, in which we need to find a lot of favorable cases, which is known as favorable events in probability jargon.
Now, finding all the cases is time consuming and might involve a lot of calculations. In such situations, we may end up making a mistake too.
Hmm...so how should we tackle such a situation? Obviously there has to be a better way to do it!
Well, the better way or better method is known as the - Non-Event Method, in which we find all the cases which we do not want (known as non-event) and subtract it from the favorable cases.
This method reduces a lot a calculation but at the same place, test your logical thinking skills.
Let’s understand what I am trying to say with the help of an example!
e-GMAT Example 1
Q--If x is to be chosen at random from the set {1,2,3,4} and y is to be chosen at random from the set {5,6,7}, what is the probability that x*y will be even?
Now, how should be we solve this question???
Solution
We know that Probability of occurring an event= \(\frac{Total\ number\ of\ ways\ in which\ the\ event\ can\ occur}{total\ outcomes}\)
- • Thus, P (x*y is even) = \(\frac{Number\ of\ ways\ x*y\ is\ even}{Total\ outcomes}\)
Thus, we need two things:
- • The number of ways in which the multiplication of x and y is an even number and,
• Total outcomes we can get, when we take all possible combinations of x and y and multiply them with each other.
Number of ways in which x *y is even
x*y can be even in three ways:
- 1. When both, x and y, are even Or,
2. When x is even, and y is odd Or,
3. When x is odd, and y is even.
Thus, total ways= Ways in which both x and y are even+ Ways in which only x is even + Ways in which only y is even
- • Total ways= \(^2C_1\)*\(^1C_1\) + \(^2C_1\)*\(^2C_1\)+\(^2C_1\)*\(^1C_1\)= 2+4+2=8
Total outcomes:
Total outcomes= Ways in which x can be selected * Ways in which y can be selected
- • Total outcomes= 4*3= 12
Thus, P (x*y is even) = \(\frac{8}{12}\)= \(\frac{2}{3}\)
Although this example was an easy one and we got 3 cases, what if first set has 8 numbers and second set had 9 numbers???
Then counting every possible case will be tedious!!
Let us now solve this question by another approach: Non-event method.
Non-event Method:
The multiplication of x and y can give only two possibilities:
- • Either x*y is even or,
• x*y is odd.
Thus, if we add the probabilities of all the possible cases then their sum should be equal to 1.
Hence,
- • P (x*y is even) + P (x*y is odd) =1 or,
• P (x*y is even) = 1 - P (x*y is odd)
Thus, if we find P (when x*y is odd) then we just need to subtract its values from 1 to get the actual answer.
And, surprisingly the number of ways when x*y is odd is only 1- When x and y both are odd!!!
- • Total ways when x*y is odd= Ways when x is odd* Ways when y is odd
• = \(^2C_1\)*\(^2C_1\)= 4
Thus, P (x*y is even) = 1- \(\frac{4}{12}\)=\(\frac{8}{12}\)
Oh!! This was easy!!!!
So, can you observe that you have to think a step ahead to visualize which method will be easy for you????
And yes, non-event method reduced our calculation too.
Thus, the learning from the above example is that whenever we see that there are lot of favorable events, we should always check if the non-events is less. And if that is the case, we should find the non-events first and then subtract it from the total cases.
Now, let’s come to come to the common type of errors that a student makes while solving the questions by non-event method.
Missing cases: Error Type 1
Let us take an interesting example. Try to solve the question first before moving to the solution. There is high possibility that you might end up making the mistake highlighted in the later part of the article.
e-GMAT Example 1
Q--In a box of 12 pens, total 3 are defective. If a customer buys 2 pens selected at random from the box., what is probability that neither pen will be defective?
Solve this question by non-event method only.
- Is your answer \(\frac{21}{22}\) or \(\frac{12}{22}\)?
Solution
If your answer is \(\frac{21}{22}\) then you marked the wrong answer. ☹
Read further to understand how to avoid such mistakes!
Do you know that I knew how did you arrived at \(\frac{21}{22}\)??
- • You must have solved using the below formula
- o P (neither pen will be defective) = 1- P (Both the pens are defective)????
If that is the case, then you made a very common error!!! You missed a few cases.
Let us see how to correctly apply non-event method in this question.
Correct approach:
Let us write all the possible cases in which customer can buy the two pens.
- • He can get both the non-defective pens Or,
• He can get 1 defective pen and 1 non-defective pen Or
• He can get both the defective pen
Since the sum of the probability of all the possible cases is 1, thus
- • P (neither pen is defective) + P (1 defective pen and 1 non-defective pen) + P (Both the pens are defective) = 1
Now, can you find P (neither pen is defective)?
- • Thus, P (neither pen is defective) = 1- P (Both the pens are defective) - P (1 defective pen and 1 non-defective pen)
Can you see the mistake you made when you solved using the formula P (neither pen will be defective) = 1- P (Both the pens are defective)????
• You missed one case. This is an error of Missing cases.
Now, we only have to calculate the values of P (None of the pen is defective) and P (1 defective pen and 1 non-defective pen) and we will have the answer.
But to arrive at the above equation of P (Both the pens are defective) you need to think logically, since GMAT tests your logical thinking skills.
Now, let us find P (Both the pens are defective) and P (1 defective pen and 1 non-defective pen).
P (Both the pens are defective):
- • P (Both the pens are defective) = \(\frac{Number\ of\ ways\ when\ both\ the\ pens\ are\ defective}{Total\ ways\ to\ pick\ two\ pens}\)
• = \(\frac{^3C_2}{^{12}C_2}\)= \(\frac{3}{66}\)= \(\frac{1}{22}\)
P (1 defective pen and 1 non-defective pen):
- • P (1 defective pen and 1 non-defective pen) =\(\frac{Number\ of\ ways\ to\ pick\ 1\ defective\ and\ 1\ non-defective\ pen}{Total\ ways\ to\ pick\ two\ pens}\)
• = \(\frac{^3C_1* ^9C_1}{^{12}C_2}\)= \(3*\frac{9}{66}\)= \(\frac{9}{22}\)
Thus, P (neither pen is defective) = 1 - \(\frac{1}{22}\) - \(\frac{9}{22}\) = 1-\(\frac{10}{22}\)= \(\frac{12}{22}\)
Key Takeaways
- 1. Before solving probability questions by the non-event method, you should come up with all the possible cases.
2. Once you write the sum of probabilities of all the possible cases equal to 1, you can easily find the answer by non-event method.
When to consider the arrangement: Error Type-2
While solving any probability question, most of the students forget that for different arrangements of a particular case, the probability is also different.
They do not consider all the arrangements and calculate the probability of one of the possible cases which results into wrong answer.
Let us understand what I am trying to say with the help of an example.
e-GMAT Example 1
Q--There are 10 solid colored balls in a box including 1 green ball and 1 yellow ball. If 3 of the balls in the box are to be chosen at random without replacement, what is the probability that three balls chosen will include the green ball but not the yellow ball?
Solution
Now, have you started thinking of all the possible cases??
If not, do not worry!!! After reading this article and practicing questions, thinking of all the possible cases will be the next step you will be doing without even realizing. ?
P (Selecting 1 green but not the yellow ball) = \(\frac{P (Select\ 1\ green\ and\ select\ 2\ solid\ colored\ balls)}{Total\ outcomes}\)
Thus,
- • Probability= P (selection of 1 green ball) * P (selecting 1st solid ball) * P (Selecting 2nd solid ball)
• We can select 1 green from 10 balls in only 1 way thus,
- o P (selection of 1 green ball) = \(\frac{1}{10}\)
- o P (selecting 1st solid ball) =\(\frac{8}{9}\)and,
o P (Selecting 2nd solid ball) = \(\frac{7}{8}\)
Thus, our answer is \(\frac{7}{90}\)???????
- • No!!!!! \(\frac{7}{90}\) is not the final answer.
But most of the students mark \(\frac{7}{90}\) as the correct answer to this question.
Let us understand why this answer is not correct.
Can you find in how many ways we can choose 3 balls such that 1 ball is green, and 2 balls are solid colored???
Let us list down the possible orders.
- • R S S
• S R S
• S S R
Total cases=3
We can also think in this way that we have three balls- 1 Red and 2 Solid colored balls. In how many we can arrange them?
- • This is similar to the case of identical objects. Thus,
- o Total ways= \(\frac{3!}{2!}\)= 3
So, there are 3 arrangements possible, but we considered only 1 case i.e R S S and calculated its probability.
So how should we go about to find the answer????
- • Should we add the probabilities of all the different cases?
- o Okay, this is a good way to solve. But what if we have a number larger than 3???
o Let’s suppose out of 15 cases we considered only 1 case then how will you find the answer???
o Will you add the probabilities of all the Cases?
o No, right!!
So, let us look at another way!
Let us first find P(S R S) and P(S S R).
- • P(S R S)=\(\frac{8}{10}*\frac{1}{9}*\frac{7}{8}\)= \(\frac{7}{90}\) = P(R S S)
• P(S S R)= \(\frac{8}{10}*\frac{1}{9}*\frac{7}{8}\)= \(\frac{7}{90}\)= P(R S S)
If you observe, then all the three cases have the same probability.
Thus, multiplying 3 with P(R S S) will give our final answer and 3 is the number of ways in which you can select 3 balls- 1 Red and 2 Solid colored balls.
Key takeaways from the example:
If we replace 3 by the number of ways balls can be arranged, then we can conclude:
- • If there are more than one arrangements possible then we will find the probability of only one case and multiply it by the total number of possible arrangements.
This will give us our final answer.
- • The first step to solve every probability question is to think of all the possible cases.
e-GMAT Example 2
Q-- A box contains 100 balls, numbered from 1 to 100.If three balls are selected at random and with replacement from the box, what is the probability that the sum of the three numbers on the three balls selected will be odd?
Solution
Can you think of all the possible cases in which we can get the sum of three numbers to be odd?
There are 2 possible cases:
- • When all the three numbers are odd or,
• When two numbers are even, and one is odd.
Probability when all the numbers are odd:
- • = P(Odd) * P(Odd) * (POdd)
• =\(\frac{1}{2}\) * \(\frac{1}{2}\) * \(\frac{1}{2}\) =\(\frac{1}{8}\)
Probability when two numbers are even, and one is odd:
- • = P(Odd) * P(Even) * P(Even)
• =\(\frac{1}{2}\)*\(\frac{1}{2}\)*\(\frac{1}{2}\)=\(\frac{1}{8}\)
However, this case can occur in 3!/2!= 3 ways.
- • Odd, Even, Even
• Even, Odd, Even
• Even, Even, Odd
Hence,
- • P(two numbers are even, and one is odd) = 3*\(\frac{1}{8}\)
Thus, total probability= \(\frac{1}{8}\)+\(\frac{3}{8}\)=\(\frac{4}{8}\)= \(\frac{1}{2}\)
Probability in dependent events:
Let us look at a slightly complex problem of probability and a question that is put so beautifully that most of the aspirants fall prey to the trap of this question and mark a wrong answer.
Do you want to test your knowledge of probability??? Let’s give it a try. ?
e-GMAT Example 1
Q--If the probability is 0.54 that stock A will increase in value during the next month and the probability is 0.68 that stock B will increase in value during the next month, what is the greatest value for the probability that neither of these two events will occur.
Solution
Is the answer equal to 0.1472 or 0.32????
If your answer is 0.1472 then this is the 3rd mistake you will avoid after reading this article. ?
Let us see why 0.1472 is wrong.
Can you observe that the language of this question is a little different???
- • In every question we are asked to find what the probability that an event can occur however, in this question, we are asked to find the greatest probability such that both the events do not occur.
• So how should we find this??
We know how to find the probability but what is greatest probability?
Well, don’t worry!! This is a question of probability where two events are dependent.
Let us understand independent and dependent events first.
Independent Events
- • We are tossing a coin two times.
- o Can we say that the occurrence of head/tail in the 2nd toss is dependent on the occurrence of head/tail in the first toss.?
o No, right! It does not matter what we get in the first toss. It won’t affect toss 2.
o This is an example of Independent events.
Dependent Events
- • Now, from the real-life experience, we all know that the prices of some stocks maybe dependent on each other.
- o If the price of one stock increases, then the price of some stocks may increase, and the price of some other stocks may decrease.
• These events are dependent events.
And our question is a perfect example of dependent events.
So, how do we calculate the greatest probability such that neither of these two events occur????
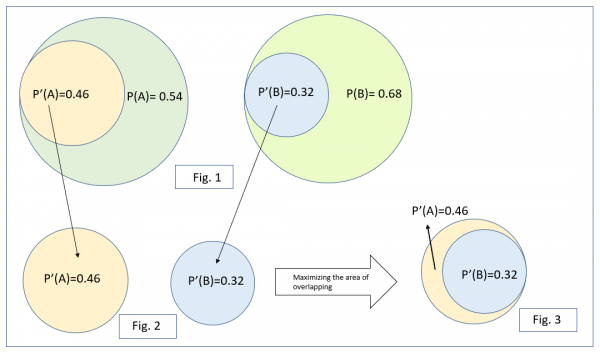
Let us see two dependent events, A and B, pictorially.
Since P(A)= 0.54, P’(A)= 0.46
This is shown pictorially below (Fig 1):

Here, the full circle represents the total probability in which all the events can occur(A might increase and decrease) and the small circle inside it represents the probability of all the events in which A can decrease .
From the diagram, we know that we need to maximize the area/probability of P’(A).
So, how can we maximize this keeping in mind that A and B are dependent???
- • How can we make the overlapping of event A’ and B’ greatest?
- o This is shown in the diagram above.(Fig 2 and Fig.3)
o Fig.2 shows the areas of A’ and B’ and now we need to figure out the maximum overlap between these two.
o And we can do so, as show in Fig. 3
- • The complete overlap of event A’ with event B’ happens:
- o when we map B’ inside A’ and “assume that when B does not increase A will also not increase at the same time.
o Hence, the probability of area such that both A and B does not occur= 0.32
o And this is the greatest probability because if we move B a little, the probability, 0.32, will reduce.
o Hence, our answer is 0.32.
This is the way to solve questions of dependent probability.
So, we learnt 3 ways to avoid mistakes while solving probability questions. Let us summarise everything.
Key Takeaways from the article
- 1. The first step to solve any probability question is to think of all the possible cases.
2. To make sure that you are not missing any cases when solving by non-event method, write the sum of probabilities of all the possible cases equal to 1 then you can easily find the answer by non-event method.
3. If there are more than one arrangements possible then we find the probability of only one case and multiply by the total number of possible arrangements.
4. Always keep an eye on the keywords like- greatest probability and minimum probability and make sure to draw diagrams to visualize the overlap between the probabilities of 2 events.
Attachments
![]() 3 mistakes to avoid in Probability.pdf [537.37 KiB]
3 mistakes to avoid in Probability.pdf [537.37 KiB]
Downloaded 546 times
Originally posted by EgmatQuantExpert on 26 Apr 2018, 04:31.
Last edited by EgmatQuantExpert on 27 Apr 2018, 06:00, edited 1 time in total.
Last edited by EgmatQuantExpert on 27 Apr 2018, 06:00, edited 1 time in total.
Kudos
Bookmarks
Hey Everyone,
Here is a list of questions specifically designed to help you apply the learnings from this article.
Exercise Questions
Question 1
Question 2
Question 3
Question 4
Detailed solutions will be posted soon.
Happy Learning!
Kudos
Bookmarks
Hey Everyone,
4 practice questions have been added.
Solve them to avoid the 3 most common mistakes in you exam.
Happly Learning.
Regards,
Ashutosh
e-GMAT
4 practice questions have been added.
Solve them to avoid the 3 most common mistakes in you exam.
Happly Learning.
Regards,
Ashutosh
e-GMAT