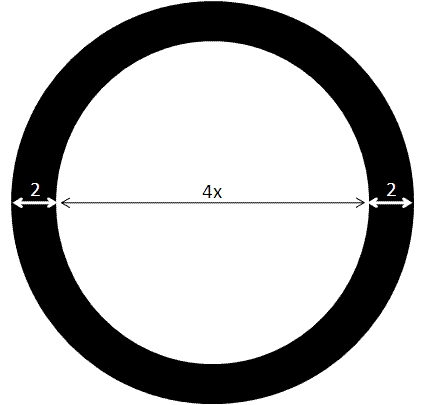
Official Solution:A circular table has a glass center with a diameter of \(4x\) inches, which is surrounded by a metal ring with a width of 2 inches. In terms of \(x\), what fraction of the table's surface is made up by the metal ring?A. \(\frac{1}{x+1}\)
B. \(\frac{1}{x}\)
C. \(\frac{x^{2}}{(x+1)^{2}}\)
D. \(\frac{2x +1}{(x+1)^{2}}\)
E. \(\frac{x}{x + 1}\)
We must determine what fraction of the table's total area (glass and metal) is made up by the metal ring. The expression we are interested in, then, is \(\frac{Area_{whole} - Area_{glass}}{Area_{whole}}\).
The formula for the area of a circle is \(A = \pi r^2\), where \(r\) is the radius of the circle. Here, we are given the diameter of the glass center. Since the radius of a circle is half its diameter, the radius of the glass is \(r_{g} = \frac{4x}{2} = 2x\) inches.
The metal ring extends 2 inches in every direction, so the diameter of the whole table is \(4x + 4\), as in the diagram below:

Thus, the radius of the whole table is \(r_{w} = \frac{4x + 4}{2} = 2x + 2\) inches.
Combine the area formula with the fraction determined above: \(\frac{Area_{whole} - Area_{glass}}{Area_{whole}} = \frac{\pi (r_{w})^2 - \pi (r_{g})^2}{\pi (r_{w})^2}\).
Plug in the values for the radii: \(\frac{\pi (2x +2)^2 - \pi (2x)^2}{\pi (2x + 2)^2}\).
Use FOIL to multiply the polynomials: \(\frac{(4x^{2} + 8x + 4)\pi - (4x^{2})\pi}{(4x^{2} + 8x + 4)\pi}\).
Factor out \(4 \pi\) from the top and bottom of the fraction and reduce: \(\frac{x^{2} + 2x + 1- x^{2}}{x^{2} + 2x + 1}\).
Simplify the numerator and factor the denominator: \(\frac{2x +1}{(x+1)^{2}}\).
Answer
choice D is correct.
Given that this approach requires some complex algebraic manipulations and that the answer choices all contain variables, we may instead choose to solve this problem by plugging in a value for \(x\). We will say that \(x = 2\). Then the diameter of the glass is \(4(2) = 8\) inches, and the radius of the glass is 4 inches. The radius of the whole table is 2 inches more, or 6 inches. Computing the fraction, we find: \(\frac{Area_{whole} - Area_{glass}}{Area_{whole}} = \frac{\pi(6)^2 - \pi(4)^2}{\pi(6)^2}\). Simplified, this is: \(\frac{36\pi - 16\pi}{36\pi} = \frac{20\pi}{36\pi}\), or \(\frac{5}{9}\).
We now substitute 2 for \(x\) in all the answer choices and see which expressions produce \(\frac{5}{9}\). Remember that we must always check all five answer choices, in case the value we picked for \(x\) produces the "right" output for two or more answer choices.
Choice A: \(\frac{1}{x+1} = \frac{1}{3}\). This is not equal to \(\frac{5}{9}\).
Choice B: \(\frac{1}{x} = \frac{1}{2}\). This is not equal to \(\frac{5}{9}\).
Choice C: \(\frac{x^{2}}{(x+1)^{2}} = \frac{4}{9}\). This is not equal to \(\frac{5}{9}\).
Choice D: \(\frac{2x +1}{(x+1)^{2}} = \frac{5}{9}\). So answer choice
D works.
Choice E: \(\frac{x}{x + 1} = \frac{2}{3}\). This is not equal to \(\frac{5}{9}\).
Answer: D.
Attachment:
 s95-21.gif [ 4.88 KiB | Viewed 8003 times ]
s95-21.gif [ 4.88 KiB | Viewed 8003 times ]
_________________



 45%
(medium)
45%
(medium)
 27%
(03:02)
wrong
27%
(03:02)
wrong  based on 206
sessions
based on 206
sessions







