Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Kudos
Bookmarks
A
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
 95%
(hard)
95%
(hard)
Question Stats:
29% (02:09) correct 71%
(02:25)
wrong
71%
(02:25)
wrong  based on 210
sessions
based on 210
sessions
History
Date
Time
Result
Not Attempted Yet
Attachment:
Capture.PNG [ 3.26 KiB | Viewed 9832 times ]
In the figure above, segment BD has length 6. What is the length of segment AC?
A. The area of quadrilateral ABCD is 60.
B. The length of segment AD is 10.
Kudos
Bookmarks
Hi Godot53,
One cardinal rule that will serve you well while solving Geometry questions on the GMAT is to 'never make assumptions'. While solving Ds questions, do not go by how the diagram looks to you, but instead look for definite pieces of information provided in the questions stem and the diagram.
The definite pieces of information provided here are
1. Angle ABD and BDC are 90 degrees
If we analyze this piece of information in depth, then we can definitely say that the lines AB and DC are parallel. When a transversal (in this case BD) cuts two lines (in this case AB and DC), the two lines are said to be parallel if ONE of the three conditions are satisfied:
1. Alternate angles are equal
2. Corresponding angles are equal
3. Sum of the interior angles is 180 degrees
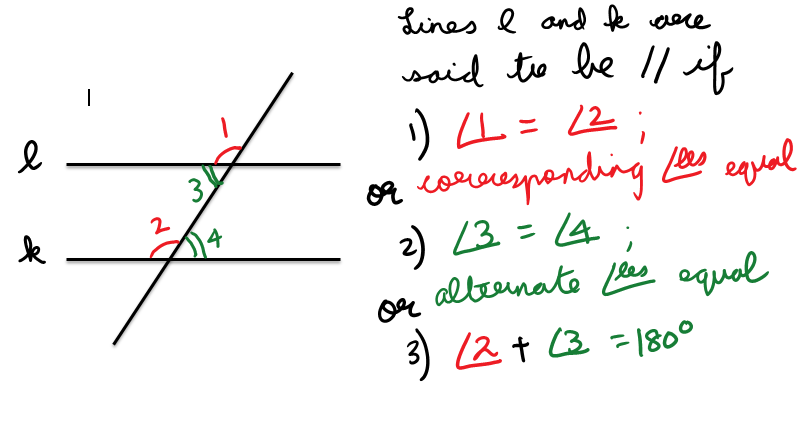
Screenshot.png [ 38.79 KiB | Viewed 9731 times ]
So here since we have angles ABD and BDC to be 90 degrees, the sum of interior angles will be 180 degrees. This makes lines AB and DC parallel.
ABCD is therefore a trapezoid whose bases are AB and CD and whose perpendicular height is BD=6.
Area of a trapezoid = (Sum of parallel sides)/2 * h
Thus, area of trapezoid ABCD = (AB+CD)/2 * 6 = 3(AB+CD)
Screenshot 2.PNG [ 14.34 KiB | Viewed 9606 times ]
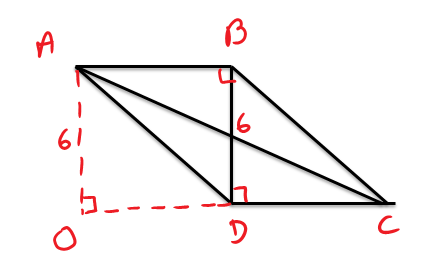
In the figure above, since AO is perpendicular to CO, quadrilateral ABDO is a rectangle and ∆ACO is a right triangle
In rectangle ABDO, AO = BD =6 and DO = AB.
OC = OD+CD ------> OC = AB + DC .
Since ∆ACE is a right triangle, AO^2 + OC^2 = AC^2 ------> 6^2 + OC^2 = AC^2.
So here we just need the length of OC or the length of AB + DC.
Statement 1: The area of quadrilateral ABCD is 60
3(AB+CD) = 60
AB+CD = 20. SUFFICIENT.
Statement 2: AD =10
Using this information we can find out AB, but we still do not know the length of DC. INSUFFICIENT.
Answer : A
Hope this helps!
CrackVerbal Academics Team
One cardinal rule that will serve you well while solving Geometry questions on the GMAT is to 'never make assumptions'. While solving Ds questions, do not go by how the diagram looks to you, but instead look for definite pieces of information provided in the questions stem and the diagram.
The definite pieces of information provided here are
1. Angle ABD and BDC are 90 degrees
If we analyze this piece of information in depth, then we can definitely say that the lines AB and DC are parallel. When a transversal (in this case BD) cuts two lines (in this case AB and DC), the two lines are said to be parallel if ONE of the three conditions are satisfied:
1. Alternate angles are equal
2. Corresponding angles are equal
3. Sum of the interior angles is 180 degrees
Attachment:
Screenshot.png [ 38.79 KiB | Viewed 9731 times ]
So here since we have angles ABD and BDC to be 90 degrees, the sum of interior angles will be 180 degrees. This makes lines AB and DC parallel.
ABCD is therefore a trapezoid whose bases are AB and CD and whose perpendicular height is BD=6.
Area of a trapezoid = (Sum of parallel sides)/2 * h
Thus, area of trapezoid ABCD = (AB+CD)/2 * 6 = 3(AB+CD)
Attachment:
Screenshot 2.PNG [ 14.34 KiB | Viewed 9606 times ]
In the figure above, since AO is perpendicular to CO, quadrilateral ABDO is a rectangle and ∆ACO is a right triangle
In rectangle ABDO, AO = BD =6 and DO = AB.
OC = OD+CD ------> OC = AB + DC .
Since ∆ACE is a right triangle, AO^2 + OC^2 = AC^2 ------> 6^2 + OC^2 = AC^2.
So here we just need the length of OC or the length of AB + DC.
Statement 1: The area of quadrilateral ABCD is 60
3(AB+CD) = 60
AB+CD = 20. SUFFICIENT.
Statement 2: AD =10
Using this information we can find out AB, but we still do not know the length of DC. INSUFFICIENT.
Answer : A
Hope this helps!
CrackVerbal Academics Team
General Discussion
Kudos
Bookmarks
Given: BD=6
Statement 1: The area of quadrilateral ABCD is 60.
Let the point where AC intersects BD be X. So, BD= BX + XD
The area of quadrilateral ABCD= Area of Triangle ABC + Area of Triangle ADC
Area of Triangle ABC= (1/2)*AC*BX
Area of Triangle ADC= (1/2)*AC*XD
On Adding, we get
Area of Triangle ABC + Area of Triangle ADC= (1/2)*AC*BX + (1/2)*AC*XD
Taking (1/2)*AC Common, we get
The area of quadrilateral ABCD= Area of Triangle ABC + Area of Triangle ADC= (1/2)*AC*[BX+DX]
60 = (1/2)*AC*BD
60= (1/2)*AC*6
We can solve for AC.
Hence, Sufficient.
Statement 1:The length of segment AD is 10.
Using AD, we can Find BC but nothing else.
hence Insufficient.
Therefore, our Answer is A.
Statement 1: The area of quadrilateral ABCD is 60.
Let the point where AC intersects BD be X. So, BD= BX + XD
The area of quadrilateral ABCD= Area of Triangle ABC + Area of Triangle ADC
Area of Triangle ABC= (1/2)*AC*BX
Area of Triangle ADC= (1/2)*AC*XD
On Adding, we get
Area of Triangle ABC + Area of Triangle ADC= (1/2)*AC*BX + (1/2)*AC*XD
Taking (1/2)*AC Common, we get
The area of quadrilateral ABCD= Area of Triangle ABC + Area of Triangle ADC= (1/2)*AC*[BX+DX]
60 = (1/2)*AC*BD
60= (1/2)*AC*6
We can solve for AC.
Hence, Sufficient.
Statement 1:The length of segment AD is 10.
Using AD, we can Find BC but nothing else.
hence Insufficient.
Therefore, our Answer is A.
godot53










