Events & Promotions
|
It is currently 19 Apr 2024, 09:16 |

Customized
for You
Track
Your Progress
Practice
Pays
10:00 AM PDT
-11:00 AM PDT
12:00 PM PDT
-01:00 PM PDT
08:30 AM PDT
-09:30 AM PDT
08:30 AM PDT
-09:30 AM PDT
11:00 AM IST
-01:00 PM IST
11:00 AM IST
-01:00 PM IST
12:00 PM EDT
-01:00 PM EDT
11:00 AM EDT
-12:00 PM EDT
06:45 AM PDT
-12:00 PM PDT
Difficulty:


 25%
(medium)
25%
(medium)
Question Stats:
80% (01:20) correct 20%
(00:51)
wrong
20%
(00:51)
wrong  based on 64
sessions
based on 64
sessions
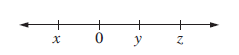

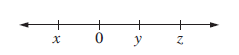







You do not have the required permissions to view the files attached to this post.
You do not have the required permissions to view the files attached to this post.



|
|
||
|
Hi Guest,
Here are updates for you:
ANNOUNCEMENTS
Tuck at Dartmouth
|