Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 04 Jul 2018, 05:59.
Last edited by EgmatQuantExpert on 13 Aug 2018, 05:15, edited 6 times in total.
Last edited by EgmatQuantExpert on 13 Aug 2018, 05:15, edited 6 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
This is the first article of our article series based on Statistics. The purpose of this article is to help you learn the most efficient way to solve any statistics question. The methods that have been taught in this article will help you solve any statistics question under a minute!
This article has been written assuming that student knows the basic formula of mean, median, mode and standard deviation. If you do not know that, then go through the basics first and then read this article.
In this article we will discuss only 2 main subtopics of statistics:
So, let’s get started!
Objective of the article
In the article, we will learn:
So, let us begin by understanding the application of arithmetic mean in 2 GMAT like questions and learn the best way to solve them. ?
Arithmetic Mean
Arithmetic mean problems can be broadly classified into 2 categories:
Let us see 1-1 example of Type 1 and Type 2.
Type 1 example:
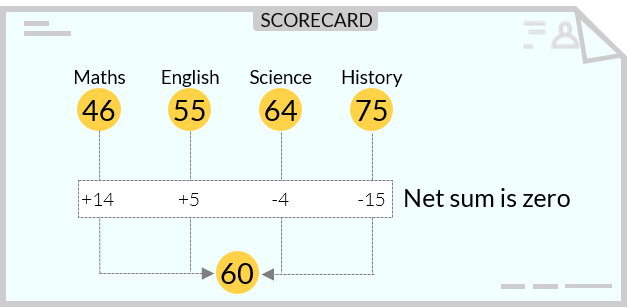
Ron scores 46, 55, 64, 75 in Math, English, Science and History tests respectively. What is the average marks scored by Ron?
Type 2 example:
In 4 tests, the average score of Ron is 60. If he scores 84 in Social Science, which is the fifth test, what is his overall average score of 5 tests?
So, can you spot the difference in both the type of questions?
However, most of the students solve both the questions in a similar way, by applying the following formula:
Let us solve both the questions and see how Type 2 question can be solved in a better way.
e-GMAT Example 1
Ron scores 46, 55, 64, 75 in Math, English, Science and History tests respectively. What is the average marks scored by Ron?
Solution
This is simple, Right?
But, let us understand what this value, 60 signifies.
So, when we say that the average is 60, we mean that we may assume all the marks to be equal to the mean, which is 60 in this case.
Let us solve our second example and see how we can use the above inference in our next question.
e-GMAT Example 2
In 4 tests, the average score of Ron is 60. If he scores 84 in Social Science, which is the fifth test, what is his overall average score of 5 tests?
Solution
You can solve this question by \(Mean= \frac{Sum\ of\ all\ the\ numbers}{Total\ Numbers}\). But remember, we are here to learn a better method to solve such questions.
Since the average is 60, we can assume Ron’s score in the previous 4 tests to be 60, 60, 60, and 60.
Therefore, if we are adding 84 in place of 60, then the average score of Ron will certainly be "60 + some extra average score".
This process may look a little complicated at first, but if you observe, then this complete process involves only 2 steps.
Let us now solve a difficult question based on the similar concept.
e-GMAT Example 3
Ron’s Average score in 5 tests is 70. What must be his score in the 6th test so that his new average score becomes 75?
Solution
Now, this is just opposite of the previous question, right?
In this question, we are asked to find out the exact score of the \(6^{th}\) test.
So, how should we solve this one? Well, don’t worry.
In the last question, we used the score to find the new average. And in this question, we need to use the new average to find the score in the 6th test.
Let’s follow the process and solve the question.
A quick observation will tell you that till 5 tests:
And right after the \(6^{th}\) test,
Now, this increase in average, which is resulted from the newly added number, must have increased the values of the previous elements also.
Now, I must emphasize over the fact that in this entire process, we did only 2 steps:
An Important Note
In the previous example that we discussed, the average of all the elements increased when a new element is added to the existing set.
What will happen if the average of all the elements decreases when a new element is added to the existing set?
In this case, the process of solving the question remains the same, with a small modification.
As the inclusion of the new number decreases the overall average, first we will find the deficit value in average.
This reduction is happening in each of the numbers which were previously present in the set.
Finally, if we subtract this cumulative deficit from the new average, we will get the value of the added element.
This may seem like a new concept, and it will take a little time to settle in. However, once you start to apply this to solve the averages question, you won’t take more than 40-50 sec to solve this question.
Let us quickly discuss the process that we followed to solve the above 2 questions and write our inferences so that we can use them to solve averages questions efficiently, and correctly.
Key Takeaways
In the first two types of questions, we saw a logical method of calculating the mean and its application.
Let us move on to our next sub-topic: Standard Deviation.
Standard Deviation
Before beginning our discussion on standard Deviation, we want you to understand the basics of it, in brief.
The general formula to find the value of standard deviation is:
 where:
where:
Note that, the process of understanding and solving a Standard Deviation question becomes easier if we use the word ‘gap’ instead of ‘difference’ or ‘deviation’. Let us solve a question to demonstrate that.
e-GMAT Example 4
The standard deviation of the elements of the set {2,3,4,5,6,7,8} is x. If we add 3 to every element of the given set, what will be the new standard deviation?
Solution
First, we will solve this question by applying the formula. Then we will look for an easier way to solve the same question.
By applying the formula:
Now, after adding 3 in all the elements of the set, we get the set as: {5,6,7,8,9,10,11}
We can see, the standard deviation is same in both the cases.
Logical way:
Here “gap” signifies the “distance between two elements” that we call as difference.
So, if you think carefully, will the gap between two elements change if we add the same number to both the elements? Let us take an example to find that out.
Can you see how easy the solving process becomes, if you think Standard Deviation in terms of the “gap” between two given elements?
Now, instead of adding the same number in all the elements, how Standard Deviation will change if we subtract the same number from all the elements?
This is a very useful inference! Let us rephrase it again so that we have a complete understanding of it.
But, before discussing it, I would like to ask you a question:
By now, you must have understood that multiplying all the numbers in a set by the same number will change the gap, and hence, the standard deviation.
Let us take one example and understand how this change will be reflected in the new standard deviation.
e-GMAT Example 5
The standard deviation of the elements of the set {2,3,4,5,6,7,8} is x. If we multiply every element of the given set by 3, what will be the new standard deviation?
Solution
We can skip the calculation of standard deviation of {2,3,4,5,6,7,8}, as we already know it is 2.
Let us calculate the standard deviation of {2*3, 3*3, 4*3, 5*6, 6*3, 7*3, 8*3}
So, if we multiply all the elements of a set by the same number, then new standard deviation will also get multiplied by the same number.
Now, before we take the next example, let me ask you another question.
Can you tell me how standard deviation will change if we divide each of the elements of a set by a constant number?
By this time, you must have guessed it correctly – you can get the standard deviation of the new elements if you divide the old standard deviation by the constant number. This is exactly similar to the case of multiplication.
That is a very important learning. So, let’s just write all that we learned about the standard deviation so far.
Key Takeaways
With these two learning, let us solve one GMAT-like question.
e-GMAT Example 6
Q--In an MBA entrance exam, scores are calculated by adjusting a student’ score using the formula y= x*\(\frac{3}{2}\)+55, where x is the original score of the student and y is the adjusted score of the student. If the standard deviation of the original scores of all the students that took the test is 450, then what will be the standard deviation of the adjusted score?
Solution
We are given that, original standard deviation of all the scores is 450.
Hence, 675 is the standard deviation of all the adjusted scores.
Key-Takeaways from the article:
Did you enjoy reading this article?
If you want to learn more about such concepts and read such articles, then click on the link below:
Read More such articles: Must Read Articles and Practice Questions to score Q51 !!!!
Next week, we will post one more article in the series of statistics: - “Solve any Median and Range question under a minute” where you will learn the concepts of Median, and Range.
With this, we have now come to the end of this article.
See you in a healthy discussion in the practice questions.
Solve any Mean and Standard deviation question under a minute
This is the first article of our article series based on Statistics. The purpose of this article is to help you learn the most efficient way to solve any statistics question. The methods that have been taught in this article will help you solve any statistics question under a minute!
This article has been written assuming that student knows the basic formula of mean, median, mode and standard deviation. If you do not know that, then go through the basics first and then read this article.
In this article we will discuss only 2 main subtopics of statistics:
- • Arithmetic Mean and
• Standard Deviation
So, let’s get started!
Objective of the article
In the article, we will learn:
- • How to solve arithmetic mean questions if one or more elements are added to a given set of numbers.
• How to easily solve standard deviation questions if we are:
- o Adding/Subtracting a constant to all the elements of the set.
o Multiplying/Dividing a constant to all the elements of the set.
So, let us begin by understanding the application of arithmetic mean in 2 GMAT like questions and learn the best way to solve them. ?
Arithmetic Mean
Arithmetic mean problems can be broadly classified into 2 categories:
- 1. When certain numbers are given, and we need to find their mean/average.
2. When mean of certain numbers are given, and one number is added/removed – and we are asked to find the new mean/average.
Let us see 1-1 example of Type 1 and Type 2.
Type 1 example:
Ron scores 46, 55, 64, 75 in Math, English, Science and History tests respectively. What is the average marks scored by Ron?
Type 2 example:
In 4 tests, the average score of Ron is 60. If he scores 84 in Social Science, which is the fifth test, what is his overall average score of 5 tests?
So, can you spot the difference in both the type of questions?
- • In the first case, we need to find the average of 4 tests, and in the second question, we are given the average of 4 tests and asked to find the new average if a 5th test is also included.
• Hence, we should be solving both the questions in a slightly different way, right?
However, most of the students solve both the questions in a similar way, by applying the following formula:
- • \(Mean= \frac{Sum\ of\ all\ the\ numbers}{Total\ Numbers}\)
Let us solve both the questions and see how Type 2 question can be solved in a better way.
e-GMAT Example 1
Ron scores 46, 55, 64, 75 in Math, English, Science and History tests respectively. What is the average marks scored by Ron?
Solution
This is simple, Right?
- • Average Marks scored by Ron= \(\frac{46+55+64+75}{4}= \frac{240}{4}= 60\).
But, let us understand what this value, 60 signifies.
- • If we assume that Ron scored equal marks in every subject, and total marks is 240, then in each subject he would have scored 60.
So, when we say that the average is 60, we mean that we may assume all the marks to be equal to the mean, which is 60 in this case.
Let us solve our second example and see how we can use the above inference in our next question.
e-GMAT Example 2
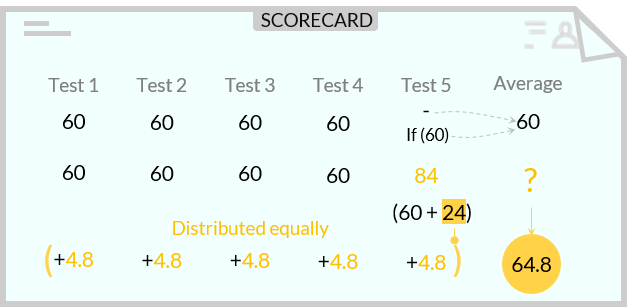
In 4 tests, the average score of Ron is 60. If he scores 84 in Social Science, which is the fifth test, what is his overall average score of 5 tests?
Solution
You can solve this question by \(Mean= \frac{Sum\ of\ all\ the\ numbers}{Total\ Numbers}\). But remember, we are here to learn a better method to solve such questions.
Since the average is 60, we can assume Ron’s score in the previous 4 tests to be 60, 60, 60, and 60.
- • Now, Ron scored 84 in the next test. So, his average scores will be calculated by calculating the average of 60, 60, 60, 60, and 84.
- But, here I have a question.
- • What if he would have scored 60 in the Social Science test too. Will his average score get changed?
- o No, still his average score would have remained 60 in all subjects.
Therefore, if we are adding 84 in place of 60, then the average score of Ron will certainly be "60 + some extra average score".
- • So, what will result in this extra average score?
- o Extra 24 in 84, right?
o Hence, we should also divide this extra 24 equally among all the 5 subjects.
• Therefore, the new average score= 60+ \(\frac{24}{5}\)= 60+4.8= 64.8.
This process may look a little complicated at first, but if you observe, then this complete process involves only 2 steps.
- 1. Breaking 84 into two parts: 60 (the old average) and the excess marks scored by Ron.
2. Distributing excess marks equally among all the subjects, including the new subject, to get the new average score.
Let us now solve a difficult question based on the similar concept.
e-GMAT Example 3
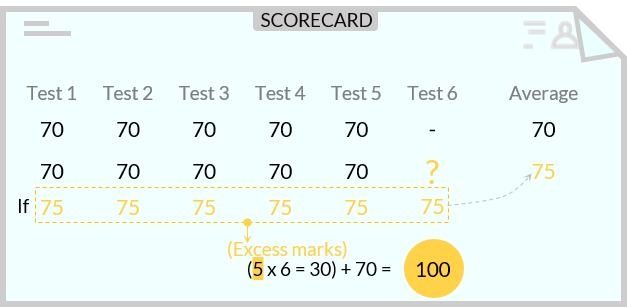
Ron’s Average score in 5 tests is 70. What must be his score in the 6th test so that his new average score becomes 75?
Solution
Now, this is just opposite of the previous question, right?
In this question, we are asked to find out the exact score of the \(6^{th}\) test.
So, how should we solve this one? Well, don’t worry.
In the last question, we used the score to find the new average. And in this question, we need to use the new average to find the score in the 6th test.
- • So, we will simply walk backward.
- o We will find the difference between the new average and the original average.
o This increase in average has also increased the values of the elements which were already present before the new number is included.
- The overall increase of previous elements = increase in the average * number of elements previously present
- Hence, the value of the newly added number = new average + increase in value
Let’s follow the process and solve the question.
A quick observation will tell you that till 5 tests:
- • Ron’s scores in 5 tests can be assumed as 70, 70, 70, 70, and 70.
And right after the \(6^{th}\) test,
- • The scores in all 6 tests can be assumed as 75, 75, 75, 75, 75, and 75.
• So, the difference between the new average and the original average = 75 – 70 = 5
- o And notice that this excess 5 is added to all the previous 5 numbers.
Now, this increase in average, which is resulted from the newly added number, must have increased the values of the previous elements also.
- • Therefore, increase in values of the previous numbers = 5 * 5 = 25
- • The actual value of the newly added number = 75 + 25 = 100
Now, I must emphasize over the fact that in this entire process, we did only 2 steps:
- • Found the difference in average and calculated the impact of that difference across all the previously existing values.
• Added this calculated change to the new average to get the actual score that changed the average.
An Important Note
In the previous example that we discussed, the average of all the elements increased when a new element is added to the existing set.
What will happen if the average of all the elements decreases when a new element is added to the existing set?
In this case, the process of solving the question remains the same, with a small modification.
As the inclusion of the new number decreases the overall average, first we will find the deficit value in average.
- • Reduction in Average = Original Average – New Average
This reduction is happening in each of the numbers which were previously present in the set.
- • Hence, the cumulative reduction = reduction in the average * original number of elements present in the set
Finally, if we subtract this cumulative deficit from the new average, we will get the value of the added element.
- • Value of the added element = New average – cumulative reduction
This may seem like a new concept, and it will take a little time to settle in. However, once you start to apply this to solve the averages question, you won’t take more than 40-50 sec to solve this question.
Let us quickly discuss the process that we followed to solve the above 2 questions and write our inferences so that we can use them to solve averages questions efficiently, and correctly.
Key Takeaways
In the first two types of questions, we saw a logical method of calculating the mean and its application.
- • In Type 1 example, we simply applied the formula of mean to get the answer and understood what Mean/Average signifies.
• In Type 2 example, we applied our learning of the previous question to solve it in an efficient way. The process is as follows:
- o Say we have a Set X, with a certain number of elements, whose average is A.
o And we add a new element(P) to this Set X.
o To find the new average, we can simply do the following:
- Take the previous average A and add the average of the excess value \(\frac{(P – A)}{Total terms}\) that comes from adding the new element.
- • Sometime the question may ask us to find out the value of the newly added number that changed the original average. There can be two specific cases for this:
- o The new average is more than the original average
- In this case, first, we will find the difference between the new and original average
Then we will calculate the cumulative increase of all the elements that were originally present in the set
Finally, we will add the cumulative increase to the new average, to find the value of the newly added number
- Again, first, we will find the difference between the new and the original average
Then we will calculate the cumulative decrease of all the elements that were originally present in the set
Finally, we will subtract the cumulative decrease from the new average, to find the value of the newly added number
Let us move on to our next sub-topic: Standard Deviation.
Standard Deviation
Before beginning our discussion on standard Deviation, we want you to understand the basics of it, in brief.
- • In statistics, Standard Deviation defines how much the date is spread out, with respect to the mean or average value.
The general formula to find the value of standard deviation is:
 where:
where:- • ‘\(x_i\)’ is the ith element of the set.
• \(\bar{x}\) is the mean of the set.
• n is total number of element in the set.
Note that, the process of understanding and solving a Standard Deviation question becomes easier if we use the word ‘gap’ instead of ‘difference’ or ‘deviation’. Let us solve a question to demonstrate that.
e-GMAT Example 4
The standard deviation of the elements of the set {2,3,4,5,6,7,8} is x. If we add 3 to every element of the given set, what will be the new standard deviation?
Solution
First, we will solve this question by applying the formula. Then we will look for an easier way to solve the same question.
By applying the formula:
- • Mean= \(\frac{2+3+4+5+6+7+8}{7}=\frac{35}{7}\) = 5
• Standard Deviation= \(\sqrt{\frac{(2-5)^2+ (3-5)^2+(4-5)^2+(5-5)^2+(6-5)^2+(7-5)^2+(8-5)^2)}{7}}= 2\)
Now, after adding 3 in all the elements of the set, we get the set as: {5,6,7,8,9,10,11}
- • Hence, new mean= \(\frac{56}{7}\)=8
• Standard Deviation= \(\sqrt{\frac{(5-8)^2+ (6-8)^2+(7-8)^2+(8-8)^2+(9-8)^2+(10-5)^2+(11-8)^2)}{7}} = 2\)
We can see, the standard deviation is same in both the cases.
- • To understand why this is happening, let us solve this question in a logical manner. Also, in this way, we will make use of the change of the word “difference” to “gap”.
Logical way:
Here “gap” signifies the “distance between two elements” that we call as difference.
So, if you think carefully, will the gap between two elements change if we add the same number to both the elements? Let us take an example to find that out.
- • Gap or difference between 2 and 5 (mean value) is 3, and even after adding 3 to both the elements, the gap between 2+3 and 5+3 remains 3.
- o This is happening as the added value 3 gets canceled with each other when we are calculating the gap. [(5 + 3) – (2 + 3) = 5 – 2 = 3]
- • So, in our question, the gap between the mean and each of the individual elements will remain the same.
- o Thus, their standard deviation will also remain the same.
o And, hence the new standard deviation will also be 2.
- See – it saved your 40 seconds as you don’t need to calculate the same value again
Can you see how easy the solving process becomes, if you think Standard Deviation in terms of the “gap” between two given elements?
Now, instead of adding the same number in all the elements, how Standard Deviation will change if we subtract the same number from all the elements?
- • The gap will still remain same – so, standard deviation won’t change.
This is a very useful inference! Let us rephrase it again so that we have a complete understanding of it.
- • If we add the same number to every element of a given set, then its standard deviation will remain same.
• Similarly, if we subtract the same number from every element of a given set, then also the standard deviation will remain same.
- With this learning, let us discuss what will happen if we multiply all the numbers of a set by the same number.
But, before discussing it, I would like to ask you a question:
- • What will happen if we multiply the gap/difference/distance between the mean and any specific element by a constant? Will the gap change or remain the same?
- o If your answer is: Yes, the gap will change, then congratulations! You are on the right way.
o However, if your answer is not correct, then remember what we did in case of addition.
- We took two numbers 2 and 5 and then added 3 with each of them.
Do the process again – but this time multiply by 3, instead of adding 3.
By now, you must have understood that multiplying all the numbers in a set by the same number will change the gap, and hence, the standard deviation.
Let us take one example and understand how this change will be reflected in the new standard deviation.
e-GMAT Example 5
The standard deviation of the elements of the set {2,3,4,5,6,7,8} is x. If we multiply every element of the given set by 3, what will be the new standard deviation?
Solution
We can skip the calculation of standard deviation of {2,3,4,5,6,7,8}, as we already know it is 2.
Let us calculate the standard deviation of {2*3, 3*3, 4*3, 5*6, 6*3, 7*3, 8*3}
- • New mean= \(\frac{2*3 + 3*3 + 4*3 + 5*6 + 6*3 + 7*3 + 8*3}{7}= \frac{3*(2+3+4+5+6+7+8)}{7}=3*5\)
• Standard Deviation= \(\sqrt{\frac{(2*3-3*5)^2+ (3*3-3*5)^2+(3*4-3*5)^2+(3*5-3*5)^2+(3*6-3*5)^2+(3*7-3*5)^2+(3*8-3*5)^2)}{7}}\)
• \(\sqrt{\frac{9(2-5)^2+ 9(3-5)^2+9(4-5)^2+9(5-5)^2+9(6-5)^2+9(7-5)^2+9(8-5)^2)}{7}} = \sqrt{9*4} = 3*2\)
• Observe that the new Standard Deviation, 3*2, is nothing but Number being multiplied * Previous Standard deviation.
So, if we multiply all the elements of a set by the same number, then new standard deviation will also get multiplied by the same number.
Now, before we take the next example, let me ask you another question.
Can you tell me how standard deviation will change if we divide each of the elements of a set by a constant number?
By this time, you must have guessed it correctly – you can get the standard deviation of the new elements if you divide the old standard deviation by the constant number. This is exactly similar to the case of multiplication.
That is a very important learning. So, let’s just write all that we learned about the standard deviation so far.
Key Takeaways
- • If we add/subtract the same number to all the numbers of a set, the standard deviation of the set will not change.
• If we multiply/divide all the numbers of a set by the same number, the standard deviation will also get multiplied/divided by the same number.
With these two learning, let us solve one GMAT-like question.
e-GMAT Example 6
Q--In an MBA entrance exam, scores are calculated by adjusting a student’ score using the formula y= x*\(\frac{3}{2}\)+55, where x is the original score of the student and y is the adjusted score of the student. If the standard deviation of the original scores of all the students that took the test is 450, then what will be the standard deviation of the adjusted score?
Solution
We are given that, original standard deviation of all the scores is 450.
- • To get the adjusted score, first, we need to multiply the original score by \(\frac{3}{2}\).
- o So, the original standard deviation will also get multiplied by \(\frac{3}{2}\).
- o No. We already know that addition of the same number to all the numbers does not change the standard deviation.
Hence, 675 is the standard deviation of all the adjusted scores.
Key-Takeaways from the article:
- • In this article, we learned the logical way of understanding mean and standard deviation, and their related applications.
• If a new number is added to an existing set of numbers, then the new average of all the numbers can be calculated as “Previous average + Excess number/ total number of elements in the set including the added one.”
• We can also calculate the value of the newly added number if we know the new average and the previous average of the given set of elements.
- o If the new average is more than the original average:
- The value of the number added = New average + Change in average * number of elements originally present in the set
- The value of the number added = New average - Change in average * number of elements originally present in the set.
• On adding/subtracting the same element with respect to all the elements of a set, its standard deviation will not change - it will remain constant.
• On multiplying/dividing every element of a set by the same number, the standard deviation of the set also gets changed in the same manner - it gets multiplied or divided by the same number.
Did you enjoy reading this article?
If you want to learn more about such concepts and read such articles, then click on the link below:
Read More such articles: Must Read Articles and Practice Questions to score Q51 !!!!
Next week, we will post one more article in the series of statistics: - “Solve any Median and Range question under a minute” where you will learn the concepts of Median, and Range.
With this, we have now come to the end of this article.
See you in a healthy discussion in the practice questions.
Attachments
![]() Solve any Mean and Standard Deviation question in a minute.pdf [578.15 KiB]
Solve any Mean and Standard Deviation question in a minute.pdf [578.15 KiB]
Downloaded 498 times
Originally posted by EgmatQuantExpert on 04 Jul 2018, 06:01.
Last edited by EgmatQuantExpert on 12 Aug 2018, 22:55, edited 1 time in total.
Last edited by EgmatQuantExpert on 12 Aug 2018, 22:55, edited 1 time in total.
Kudos
Bookmarks
Hey Everyone,
Here is a list of questions specifically designed to help you apply the learnings from this article.
Exercise Questions
Question 1
Question 2
Question 3
Question 4
Question 5
Detailed solutions will be posted soon.
Happy Learning!
Kudos
Bookmarks
Official solutions for all the 5 practice questions have been posted.
Happy learning
Happy learning