Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
We are starting this thread to show how we can solve complex divisibility problems and inequalities using the basic properties of a number line.
1: Consecutive numbers and divisibility by 2, 4 and 8:
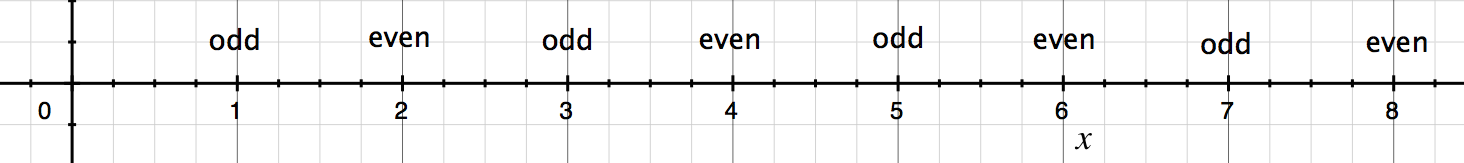
no. line 1.png [ 27.38 KiB | Viewed 30825 times ]
Few facts to note:
Let's consider a product of any three consecutive numbers n(n+1)(n+2)
Case 1: n is odd:
n(n+1)(n+2) -> odd * even * odd
Takeaway: The product of three consecutive numbers n(n+1)(n+2) is definitely divisible by 2 if n is odd.
Case 2: n is even:
n(n+1)(n+2) -> even * odd * even
n and n+2 are two consecutive even numbers. As we know between two consecutive even numbers, one is divisible by 4 and other is only divisible by 2 and not 4. Hence, n(n+2) will be divisible by 2, 4 and 2*4 =8
Takeaway: The product of three consecutive numbers n(n+1)(n+2) is definitely divisible by 2, 4 and 8 if n is even.
In this case we can also say the last two digits of the product are divisible by 4 (a number is only divisible by 4 if its last two digits are) and the last three digits of the product are divisible by 8 (a number is only divisible by 8 if its last three digits are)
Please bookmark this post and follow PrepTap if you want to receive updates on this topic.
1: Consecutive numbers and divisibility by 2, 4 and 8:
Attachment:
no. line 1.png [ 27.38 KiB | Viewed 30825 times ]
Few facts to note:
- 1. On a number line, odd and even numbers alternate. For example: 1 is odd, 2 is even. So, for any two consecutive number one will be odd and the other even.
2. Between two consecutive even numbers, one will be divisible by 4 and the other will only be divisible by 2 and not by 4.
For example:
2 and 4 -> 2 is not divisible by 4 but 4 is.
4 and 6 -> 4 is divisible by 4 but 6 is not.
Let's consider a product of any three consecutive numbers n(n+1)(n+2)
Case 1: n is odd:
n(n+1)(n+2) -> odd * even * odd
Takeaway: The product of three consecutive numbers n(n+1)(n+2) is definitely divisible by 2 if n is odd.
Case 2: n is even:
n(n+1)(n+2) -> even * odd * even
n and n+2 are two consecutive even numbers. As we know between two consecutive even numbers, one is divisible by 4 and other is only divisible by 2 and not 4. Hence, n(n+2) will be divisible by 2, 4 and 2*4 =8
Takeaway: The product of three consecutive numbers n(n+1)(n+2) is definitely divisible by 2, 4 and 8 if n is even.
In this case we can also say the last two digits of the product are divisible by 4 (a number is only divisible by 4 if its last two digits are) and the last three digits of the product are divisible by 8 (a number is only divisible by 8 if its last three digits are)
Please bookmark this post and follow PrepTap if you want to receive updates on this topic.
2: Consecutive numbers and divisibility by 3 and 6:
On a number line every nth number is divisible by n (n, 2n, 3n….)
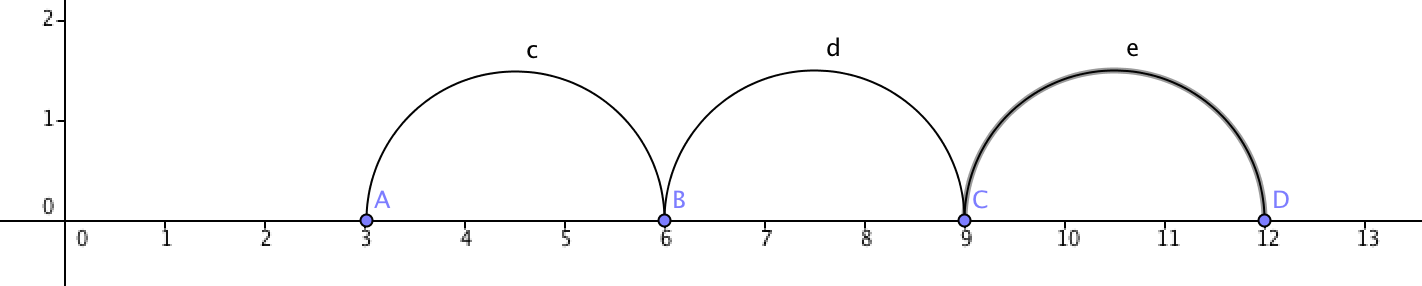
No. line muliples of 3.png [ 36.12 KiB | Viewed 30567 times ]
E.g.: Every 3rd number is divisible by 3 (3, 6, 9…)
Every 4th number is divisible by 4 (4, 8, 12..)
As every third number is divisible by 3, any number n on the number line:
-> Is either, divisible by 3 (it is of the form 3k)
-> Or, leaves a remainder 1 when divided by 3 (it is of the form 3k + 1) - in this case n+2 will be divisible by 3
-> Or, leaves a remainder 2 when divided by 3 (it is of the form 3k+2) - in this case n+1 will be divisible by 3
Hence, the product of three consecutive numbers n(n+1)(n+2) will always be divisible by 3.
As discussed in the previous post, the product of three consecutive numbers is always divisible by 2. So, the product of three consecutive numbers will always be divisible by 2*3 = 6 as well.
Takeaway: a product of three consecutive numbers is always divisible by 3 and 6.
We can also say that the sum of the digits of the product is divisible by 3 (a number is only divisible by 3 if the sum of its digits is divisible by 3)
Now, let’s consider the product of three numbers of the form:
(n +/- 3k)(n +1 +/- 3l)(n + 2 +/- 3m), where k, l and m are integers.
As you can see, a multiple of three is added to the individual numbers in the product of consecutive integers n(n+1)(n+2).
For example: 4 * 8 * 6
It is of the form (4) * (5 + 3) * (6) - > 3 is added to the middle number in the product of consecutive numbers 4*5*6
(4) * (5 + 3) * (6) = 4 * 5 * 6 + 4 * 3 * 6
This is clearly divisible by 3
(n +/- 3k)(n +1 +/- 3l)(n + 2 +/- 3m) = n(n+1)(n+2) + terms divisible by 3
As the product of three consecutive numbers is always divisible by 3, the above product is divisible by 3.
Takeaway: the product of three numbers of the form (n +/- 3k)(n +1 +/- 3l)(n + 2 +/- 3m) is always divisible by 3.
You can use this property for solving OG 13 PS Question 87
If n is an integer greater than 6, which of the following must be divisible by 3 ?
Option (A) - n(n+1)(n-4) = n(n+1) (n+2 - 6) (as n>6, this product will be positive)
As you can see this product is of the form n(n+1)(n+2 - 3*2)
It is divisible by 3.
Answer: Option (A)
Please bookmark this post and follow PrepTap if you want to receive updates on this topic.
On a number line every nth number is divisible by n (n, 2n, 3n….)
Attachment:
No. line muliples of 3.png [ 36.12 KiB | Viewed 30567 times ]
E.g.: Every 3rd number is divisible by 3 (3, 6, 9…)
Every 4th number is divisible by 4 (4, 8, 12..)
As every third number is divisible by 3, any number n on the number line:
-> Is either, divisible by 3 (it is of the form 3k)
-> Or, leaves a remainder 1 when divided by 3 (it is of the form 3k + 1) - in this case n+2 will be divisible by 3
-> Or, leaves a remainder 2 when divided by 3 (it is of the form 3k+2) - in this case n+1 will be divisible by 3
Hence, the product of three consecutive numbers n(n+1)(n+2) will always be divisible by 3.
As discussed in the previous post, the product of three consecutive numbers is always divisible by 2. So, the product of three consecutive numbers will always be divisible by 2*3 = 6 as well.
Takeaway: a product of three consecutive numbers is always divisible by 3 and 6.
We can also say that the sum of the digits of the product is divisible by 3 (a number is only divisible by 3 if the sum of its digits is divisible by 3)
Now, let’s consider the product of three numbers of the form:
(n +/- 3k)(n +1 +/- 3l)(n + 2 +/- 3m), where k, l and m are integers.
As you can see, a multiple of three is added to the individual numbers in the product of consecutive integers n(n+1)(n+2).
For example: 4 * 8 * 6
It is of the form (4) * (5 + 3) * (6) - > 3 is added to the middle number in the product of consecutive numbers 4*5*6
(4) * (5 + 3) * (6) = 4 * 5 * 6 + 4 * 3 * 6
This is clearly divisible by 3
(n +/- 3k)(n +1 +/- 3l)(n + 2 +/- 3m) = n(n+1)(n+2) + terms divisible by 3
As the product of three consecutive numbers is always divisible by 3, the above product is divisible by 3.
Takeaway: the product of three numbers of the form (n +/- 3k)(n +1 +/- 3l)(n + 2 +/- 3m) is always divisible by 3.
You can use this property for solving OG 13 PS Question 87
If n is an integer greater than 6, which of the following must be divisible by 3 ?
- (A) n(n+1)(n-4)
(B) n(n+2)(n-1)
(C) n(n+3)(n-5)
(D) n(n+4)(n-2)
(E) n(n+5)(n-6)
Option (A) - n(n+1)(n-4) = n(n+1) (n+2 - 6) (as n>6, this product will be positive)
As you can see this product is of the form n(n+1)(n+2 - 3*2)
It is divisible by 3.
Answer: Option (A)
Please bookmark this post and follow PrepTap if you want to receive updates on this topic.
Kudos
Bookmarks
4. Absolute Values and the Number Line
On a number line, \(|x-a|\) denotes the distance between x and a irrespective of the signs of x and a.
Case 1: x and a are positive
Let's say x = 1 and a = 3
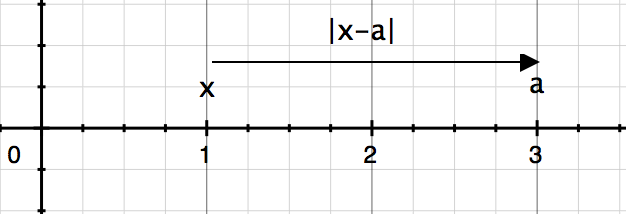
x and a positive.png [ 15.09 KiB | Viewed 30078 times ]
|x-a| = |1 - 3| = |-2| = 2
The distance remains the same when the values of x and a are swapped.
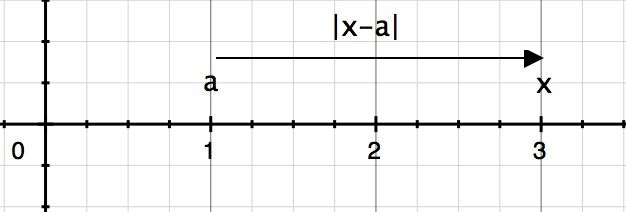
x and a positive 2.png [ 14.91 KiB | Viewed 30107 times ]
Case 2: x and a are negative
Let's say x = -1 and a = -3
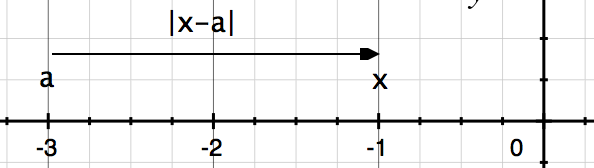
x and a negative.png [ 13.67 KiB | Viewed 29836 times ]
|x-a| = |-1 + 3| = |2| = 2
The distance remains the same when the values of x and a are swapped.
Case 3: x and a have opposite signs
|x - a| won't change as long as the distance between x and a is the same.
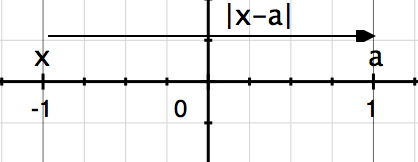
x negative a positive.png [ 10.85 KiB | Viewed 29775 times ]
Takeaway: To calculate |x - a|, find out the distance between x and a on the number line, irrespective of the signs of x and a.
Now let's take a look at an inequality involving absolute values using the number line.
|x - a| > |x - b| > |x - c|
All this inequality is saying that the distance between x and a is greater than the distance between x and b, which in turn is greater than the distance between x and c.
This is true whether x, a, b and c are positive, negative or zero.
Therefore, all the arrangements illustrated below are possible where the distances satisfy the inequality above.
x c b a
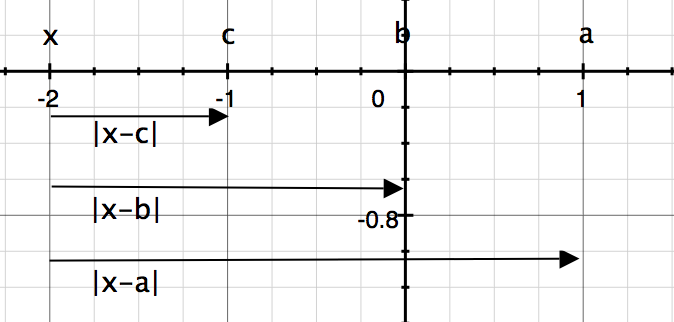
x c b a.png [ 25.34 KiB | Viewed 29679 times ]
a b c x
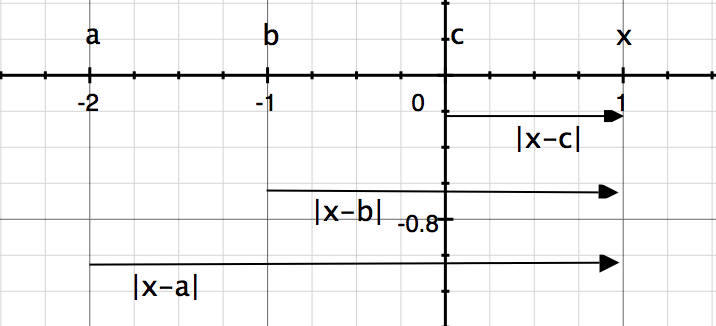
a b c x.png [ 26.28 KiB | Viewed 29712 times ]
c x b a
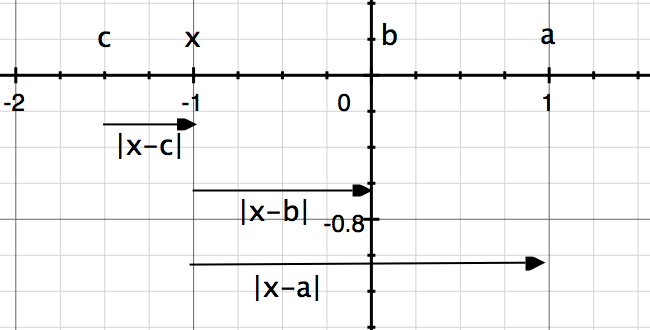
c x b a.png [ 25.62 KiB | Viewed 29639 times ]
a b x c
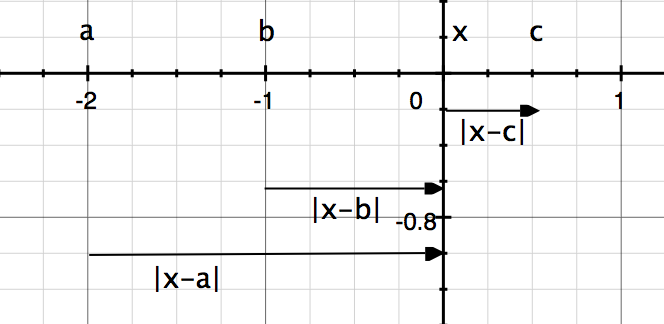
a b x c.png [ 23.94 KiB | Viewed 29630 times ]
b x c a

b x c a.png [ 25.16 KiB | Viewed 29600 times ]
a c x b
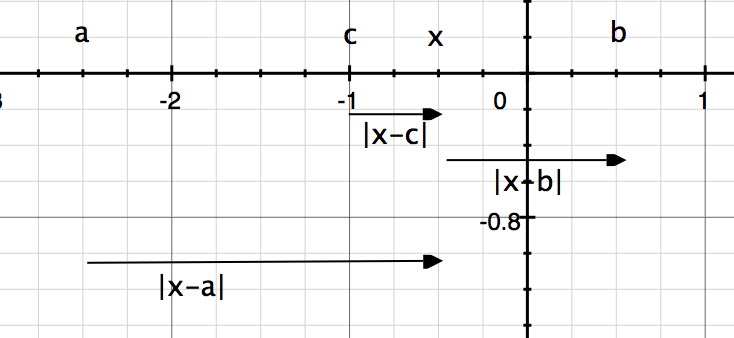
a c x b.png [ 26.47 KiB | Viewed 29602 times ]
It doesn't matter whether a, b, and c are to the left or to the right of x as long as the inequality regarding distances is maintained.
In the arrangement of a, b, c and x, the farthest point from x (namely a) will always be at one of the edges and never in the middle. Think about it and you'll see why this is so.
Also, if b and c are on the same side of x, c will always lie between x and b, i.e. these two arrangements -> c b x a and a x b c are not valid.
Takeaway: An inequality like |x - a| > |x - b| > |x - c| doesn't mean a > b > c or a < b < c. It only means either a < b, c or a > b, c. The relationship between b and c can't be established unless more information is provided.
Please bookmark this post and follow PrepTap if you want to receive updates on this topic.
On a number line, \(|x-a|\) denotes the distance between x and a irrespective of the signs of x and a.
Case 1: x and a are positive
Let's say x = 1 and a = 3
Attachment:
x and a positive.png [ 15.09 KiB | Viewed 30078 times ]
The distance remains the same when the values of x and a are swapped.
Attachment:
x and a positive 2.png [ 14.91 KiB | Viewed 30107 times ]
Case 2: x and a are negative
Let's say x = -1 and a = -3
Attachment:
x and a negative.png [ 13.67 KiB | Viewed 29836 times ]
The distance remains the same when the values of x and a are swapped.
Case 3: x and a have opposite signs
|x - a| won't change as long as the distance between x and a is the same.
Attachment:
x negative a positive.png [ 10.85 KiB | Viewed 29775 times ]
Takeaway: To calculate |x - a|, find out the distance between x and a on the number line, irrespective of the signs of x and a.
Now let's take a look at an inequality involving absolute values using the number line.
|x - a| > |x - b| > |x - c|
All this inequality is saying that the distance between x and a is greater than the distance between x and b, which in turn is greater than the distance between x and c.
This is true whether x, a, b and c are positive, negative or zero.
Therefore, all the arrangements illustrated below are possible where the distances satisfy the inequality above.
x c b a
Attachment:
x c b a.png [ 25.34 KiB | Viewed 29679 times ]
a b c x
Attachment:
a b c x.png [ 26.28 KiB | Viewed 29712 times ]
c x b a
Attachment:
c x b a.png [ 25.62 KiB | Viewed 29639 times ]
a b x c
Attachment:
a b x c.png [ 23.94 KiB | Viewed 29630 times ]
b x c a
Attachment:
b x c a.png [ 25.16 KiB | Viewed 29600 times ]
a c x b
Attachment:
a c x b.png [ 26.47 KiB | Viewed 29602 times ]
It doesn't matter whether a, b, and c are to the left or to the right of x as long as the inequality regarding distances is maintained.
In the arrangement of a, b, c and x, the farthest point from x (namely a) will always be at one of the edges and never in the middle. Think about it and you'll see why this is so.
Also, if b and c are on the same side of x, c will always lie between x and b, i.e. these two arrangements -> c b x a and a x b c are not valid.
Takeaway: An inequality like |x - a| > |x - b| > |x - c| doesn't mean a > b > c or a < b < c. It only means either a < b, c or a > b, c. The relationship between b and c can't be established unless more information is provided.
Please bookmark this post and follow PrepTap if you want to receive updates on this topic.







