Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
11:00 AM EST
-11:59 PM EST
Don’t miss Target Test Prep’s biggest sale of the year! Grab 25% off any Target Test Prep GMAT plan during our Black Friday sale. Just enter the coupon code BLACKFRIDAY25 at checkout to save up to $625. - Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 22
12:00 PM PST
-12:30 PM PST
olve GRE practice problems covering Quantitative reasoning, Verbal Reasoning, Text Completion, Sentence Equivalence, and Reading Comprehension Problems. Take this GRE practice quiz live with peers, analyze your GRE study progress, - Nov 23
10:00 AM PST
-11:00 AM PST
GMAT practice session and solve 30 challenging GMAT questions with other test takers in timed conditions, covering GMAT Quant, Data Sufficiency, Data Insights, Reading Comprehension, and Critical Reasoning questions. - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 30
10:00 AM EST
-11:59 PM EST
Get $325 off the TTP OnDemand GMAT masterclass by using the coupon code BLACKFRIDAY25 at checkout. If you prefer learning through engaging video lessons, TTP OnDemand GMAT is exactly what you need.
Kudos
Bookmarks
D
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
 55%
(hard)
55%
(hard)
Question Stats:
66% (02:29) correct 34%
(02:33)
wrong
34%
(02:33)
wrong  based on 1704
sessions
based on 1704
sessions
History
Date
Time
Result
Not Attempted Yet
The line represented by the equation y = 4 – 2x is the perpendicular bisector of line segment RP. If R has the coordinates (4, 1), what are the coordinates of point P?
(A) (–4, 1)
(B) (–2, 2)
(C) (0, 1)
(D) (0, –1)
(E) (2, 0)
(A) (–4, 1)
(B) (–2, 2)
(C) (0, 1)
(D) (0, –1)
(E) (2, 0)
How come the answer will be D? This is how I am trying to solve this.
First, rewrite the line y=4-2x as y = -2x+4 The equation is now in the form y = mx+b where m represents the slope and b represents the y-intercept.Thus, the slope of this line is -2. By definition, if a line is the perpendicular bisector of any line, the slope of line which is perpendicular bisector is the negative inverse of the slope of line G. Since we are told that the line y = -2x+4 is the perpendicular bisector of line segment RP, line segment RP
must have a slope of \(\frac{1}{2}\) (which is the negative inverse of slope of line y).
Now we know that the slope of the line containing segment RP is\(\frac{1}{2}\) but we do
not know its y-intercept. We can write the equation of this line as , y = 1/2x+b, where b represents the unknown y-intercept.
To solve for b, we can use the given information that the coordinates of point R
are (4, 1). Since point R is on the line y = 1/2x+b, we can plug 4 in for x and 1 in for y to get b = -1
Therefore, equation of line RP will become y = 1/2x-1
Also , y = -2x +4 (Equation of perpendicular bisector) -----------------(2)
Equating the two we will get x =2 . Putting this value of x in we get y = 0.
So the points should be (2,0) i.e. answer E.
Where I am getting this wrong guys?
First, rewrite the line y=4-2x as y = -2x+4 The equation is now in the form y = mx+b where m represents the slope and b represents the y-intercept.Thus, the slope of this line is -2. By definition, if a line is the perpendicular bisector of any line, the slope of line which is perpendicular bisector is the negative inverse of the slope of line G. Since we are told that the line y = -2x+4 is the perpendicular bisector of line segment RP, line segment RP
must have a slope of \(\frac{1}{2}\) (which is the negative inverse of slope of line y).
Now we know that the slope of the line containing segment RP is\(\frac{1}{2}\) but we do
not know its y-intercept. We can write the equation of this line as , y = 1/2x+b, where b represents the unknown y-intercept.
To solve for b, we can use the given information that the coordinates of point R
are (4, 1). Since point R is on the line y = 1/2x+b, we can plug 4 in for x and 1 in for y to get b = -1
Therefore, equation of line RP will become y = 1/2x-1
Also , y = -2x +4 (Equation of perpendicular bisector) -----------------(2)
Equating the two we will get x =2 . Putting this value of x in we get y = 0.
So the points should be (2,0) i.e. answer E.
Where I am getting this wrong guys?
Kudos
Bookmarks
Hello,
This is how I solved the problem. Since the Slope of line is -2, the line perpendicular to it would have SLope as 1/2. So I used R(4,1) and each options to see which one gives Slope as 1/2. Only option D gives me the co ordinates through which the SLope is 1/2. It took me around a minutes time to solve.
Please let me know if I'm correct ?
This is how I solved the problem. Since the Slope of line is -2, the line perpendicular to it would have SLope as 1/2. So I used R(4,1) and each options to see which one gives Slope as 1/2. Only option D gives me the co ordinates through which the SLope is 1/2. It took me around a minutes time to solve.
Please let me know if I'm correct ?
Kudos
Bookmarks
The line represented by the equation y = 4 – 2x is the perpendicular bisector of line segment RP. If R has the coordinates (4, 1), what are the coordinates of point P?
A. (–4, 1)
B. (–2, 2)
C. (0, 1)
D. (0, –1)
E. (2, 0)
Again, there is no need of equations to solve this question. Plot the line y = 4 – 2x (just find the x and y intercepts and draw the line through them): 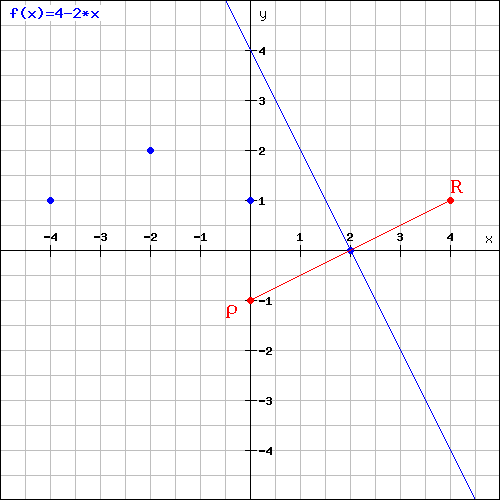
Bisector.png [ 16 KiB | Viewed 65120 times ]
Now, it's easy to SEE that no blue point can be the mirror reflection of R around the line but (0, -1).
Answer: D.
P.S. Answer cannot possibly be E (2, 0) as this point lies on the line y=4-2x (substitute the values of x and y to see that it's true).
A. (–4, 1)
B. (–2, 2)
C. (0, 1)
D. (0, –1)
E. (2, 0)
Again, there is no need of equations to solve this question. Plot the line y = 4 – 2x (just find the x and y intercepts and draw the line through them):
Attachment:
Bisector.png [ 16 KiB | Viewed 65120 times ]
Answer: D.
P.S. Answer cannot possibly be E (2, 0) as this point lies on the line y=4-2x (substitute the values of x and y to see that it's true).














