Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
himanshuhpr
Joined: 29 Aug 2012
Last visit: 28 Nov 2014
Posts: 24
Given Kudos: 56
Schools: Babson '14
GMAT Date: 02-28-2013
Kudos
Bookmarks
C
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
 95%
(hard)
95%
(hard)
Question Stats:
44% (02:17) correct 56%
(02:09)
wrong
56%
(02:09)
wrong  based on 315
sessions
based on 315
sessions
History
Date
Time
Result
Not Attempted Yet
A certain computer program randomly generates equation of line is form of y=mx+b.If point p is a point on a line generated by this prog, what is probability that line does not pass through ABCD.
A. 3/4
B. 3/5
C. 1/2
D. 2/5
E. 1/4
Attachment:
File comment: Given Figure
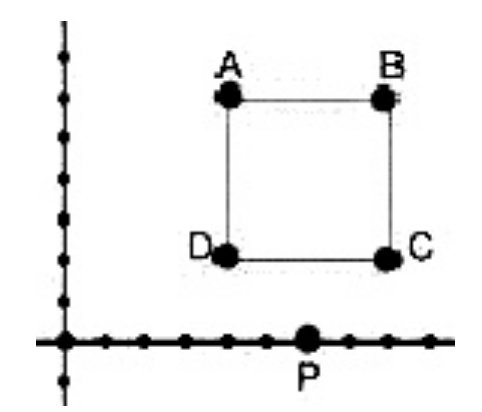
Fullscreen capture 21112012 164010.bmp.jpg [ 24.11 KiB | Viewed 20422 times ]
Fullscreen capture 21112012 164010.bmp.jpg [ 24.11 KiB | Viewed 20422 times ]
Kudos
Bookmarks
himanshuhpr
The thought was this:
Attachment:
Ques3.jpg [ 9.63 KiB | Viewed 19933 times ]
Any line passing through the point P which is at 6 on the x axis will pass through one of the 4 equal dotted regions (except x axis). Out of these, lines passing through 2 of the regions are not acceptable (red lines) while those passing through other 2 are acceptable (green lines).
Hence, 1/2 of the region is fine.
Probability that the line does not pass through ABCD is 1/2.
General Discussion
Kudos
Bookmarks
himanshuhpr
I am responding to a pm from himanshuhpr.
First of all, I am intrigued by the solution of the very intelligent VeritasPrepKarishma, for whom I have considerable respect. Nevertheless, I beg to differ.
I believe there are some significant flaws in the question. First of all, the grammar is embarrassingly atrocious, but we'll let that pass. More to the point === we are told that the program "randomly" generates lines --- how exactly is this process randomized? For example, the line goes through P --- Are all slopes equally likely? Or are all angles equally likely? If we select P and a y-intercept, are all y-intercept equally likely? Are we randomly selecting one other point in the x-y plane, and all of those points are equally likely? Those are four different ways of specifying the probabilistic process, and I believe at least some of them give different numerical answer to the question. As soon as the thing you are specifying (here, a line) can be specified in a variety of ways, its not enough to say "random" --- you have to specify exactly how the selection process proceeds.
Because the question does not specify the details of the probabilistic selection process, I believe it is a fundamentally flawed question.
Does that make sense?
Mike











