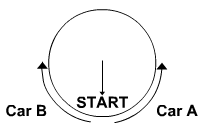
In the figure above, car A and car B simultaneously begin traveling ar

Took me 6 minutes to find the trick to avoid serious calculations.

1256=314*4.. Pie= 3.14 (approx)

pie*r sq= 1256 This will give R as 20.

Circumfrence of the circle is the total distance that the cars will travel= 2*pie*r=40* 3.14

since two cars are moving towards each other we can consider that 1 car is moving at speed of 100=60+40 miles while the other is stationary (Relative motion). Hence to meet the moving will cover the whole circumference of the circle.

Thus time =40*3.14/100 No need to calculate. This will be slightly more than 1.2 hrs. the only answer between 1 and 2 hrs is 75 minutes.

Thus answer is C

OFFICIAL SOLUTION:

(C) To visualize this question, think about a circle as just a line segment joined at its two ends. Let’s first cut the circle at the starting point and make it into a straight line. Notice that cars A and B are at opposite ends of the line traveling toward each other.

A [ ______________________ ] B

We know that the area of the circular park is 1256 square miles and that the area of a circle is equal to πr². So, 1256 = πr². Divide by 3.14, our approximation of π.

1256/3.14 = 400 = r².r = 20 miles.

Now, solve for the circumference of the park: C = 2πr. Plugging 20 into the equation, we get:C = 2 × 3.14 × 20 = 125.6 miles.

To calculate how long it takes to meet, combine the speeds of car A and car B to see how long it would take them to travel 125.6 miles.

Car A and car B are traveling toward each other at the rate of 40 + 60 = 100 miles per hour (because they are heading toward each other, we add their speeds together). At 100 mph, it will take them 1.256 hours to travel 125.6 miles and meet up.

Multiply 1.256 hours by 60 (because there are 60 minutes in one hour, and we are looking for the answer in minutes): 1.256 × 60, which is approximately 75 minutes.

The correct answer is choice (C).

distance the cars have to travel = circumference of the circle = 2pir
given area = pir^2=1256
r^2=1256*7/22 = 400
r=20
therefore distance = 2pir=40*22/7= ~126
time taken = relative distance /relative speed = 126/100 = 1.26 hours ~ 1 hour 15 minutes = 75 minutes

Area if the circle,
pi*\(r^2\) = 1256,
\(\frac{22}{7}\)*\(r^2\)=1256
we can generalize 1256 = 8*157, since the options are have a margin of at least 10 points we can write it as 9*154 to ease up the calculations.
\(\frac{22}{7}\)*\(r^2\)=9*22*7
Solving further we get, r=21.

So the time taken (in minutes) by both cars to meet will be:

\(\frac{22}{7}\)*2*21*\(\frac{60}{100}\)

(100 = 40+60, cumulative speed of the cars)

Solving further we get time = 75.6 mins ~ 75 mins

Option C

Hello from the GMAT Club BumpBot!

Thanks to another GMAT Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).

Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.