Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Kudos
Bookmarks
smodak
Detailed video solution explaining the method to approach question rightly is mentioned below
The primary method to be used to answer the question is explained after 2:18 minutes though it's recommended that viewers watch it completely.
Answer: Option E
Kudos
Bookmarks
Bunuel
Bunuel what if the tree was 2 meters? would we still take a line and divide it with the LCM 15? And once we get 3/5 we would do 3/5 * 15 = 9meters?
kaladin123

Current Student
Joined: 06 Jul 2019
Last visit: 10 Jul 2022
Posts: 135
Given Kudos: 747
Location: India
Concentration: General Management, Strategy
Schools: IIMA PGPX'23 (II)
GMAT 1: 640 Q39 V39

GMAT 2: 700 Q48 V38 (Online)

GPA: 3.11
WE:Project Management (Computer Software)
Kudos
Bookmarks
I got this question wrong in an MGMAT CAT.
However, I was able to solve it later during review.
My approach was to draw a number line and mark off the thirds and the fifths, as shown below:
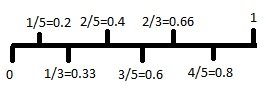
nl.jpg [ 8.46 KiB | Viewed 1321 times ]
I used the decimal equivalents to help me arrange the fractions on the number-line.
Now, it is tempting to calculate the differences of the decimal values. The challenge with this approach is that fractions like 1/3, 2/3, etc. might lead to rounding errors later.
In summary, I think that Bunuel's approach using LCM is the the perfect way to solve such a problem.
The same number line, now on a scale of [0-15]:
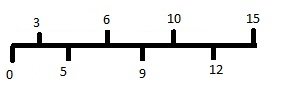
nl2.jpg [ 4.94 KiB | Viewed 1328 times ]
Difference={3, 2, 1, 3, 1, 2, 3}
We need to take away the 1st piece of each distinct length.
Fraction of original branch left=\(\frac{3+1+2+3}{15}=\frac{9}{15}=\frac{3}{5}\)
However, I was able to solve it later during review.
My approach was to draw a number line and mark off the thirds and the fifths, as shown below:
Attachment:
nl.jpg [ 8.46 KiB | Viewed 1321 times ]
Now, it is tempting to calculate the differences of the decimal values. The challenge with this approach is that fractions like 1/3, 2/3, etc. might lead to rounding errors later.
In summary, I think that Bunuel's approach using LCM is the the perfect way to solve such a problem.
The same number line, now on a scale of [0-15]:
Attachment:
nl2.jpg [ 4.94 KiB | Viewed 1328 times ]
Difference={
We need to take away the 1st piece of each distinct length.
Fraction of original branch left=\(\frac{3+1+2+3}{15}=\frac{9}{15}=\frac{3}{5}\)







