Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 30 May 2018, 03:39.
Last edited by EgmatQuantExpert on 13 Aug 2018, 00:08, edited 5 times in total.
Last edited by EgmatQuantExpert on 13 Aug 2018, 00:08, edited 5 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
This is the 2nd and the final article on the topic Time and Work. If you have not read the previous article, we recommend you read that first before going through this article.
To read the article: Solve Time and Work Problems Efficiently using Efficiency Method!
Highlights of the previous article
In the previous article, we discussed:
Objective of this article
The primary objective of this article is to cite 3 most common mistakes made by students while solving problems on Time and Work. We will demonstrate them with different examples on each type. For students’ convenience, we have referred to examples similar to what are provided in the official resources.
Common mistake type 1: Incorrect use of the relationship between efficiency and time taken
e-GMAT Example 1
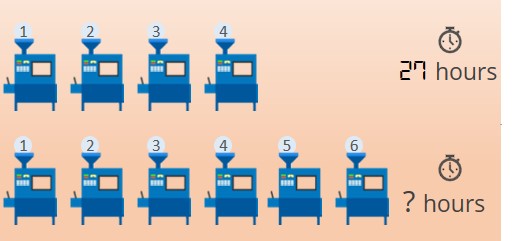
Six machines at a certain factory operate at the same constant rate. If four of these machines, operating simultaneously, take 27 hours to fill a certain production order, how many fewer hours does it take all six machines, operating simultaneously, to fill the same production order?
Common approach used by students
In this question it is given that
Now, it is given that,
If you have got 13.5 hours as the answer, then you have solved it incorrectly.
Let us take another similar example before discussing the mistake and the solution.
e-GMAT Example 2
Six machines, each working at the same constant rate, together can complete a certain job in 12 days. How many additional machines, each working at the same constant rate, will be needed to complete the job in 8 days?
Common approach used by students
In this question, it is given that:
Now it is given that,
If you have got 4 as the answer, then you have solved it incorrectly.
The mistakes and the correct approach
The error made in both the questions are very similar in nature, and the most common type of error that students make while solving. Let us look into the detail of them:
Error in Question 1
In the first question, when we are calculating the time taken by 1 machine to complete the production order, we have made a logical error.
It is given that all machines operate at the same working rate.
Error in Question 2
The solution of this question contains 2 errors.
Error 1: Same as the previous question, if 6 machines can complete the job in 12 days, then 1 machine will be completing it by taking 6 times the original time.
Error 2: Moreover, if 1 machine can complete the job in 2 days, you don’t need 4 machines to complete the job in 8 days – as 1 machine itself can complete it in 2 days’ time.
The Correct Solution – Question 1
Given that,
The Correct Solution – Question 2
Given that,
Common mistake type 2: The Incorrect Approach
e-GMAT Example 3
At his regular hourly rate, Don had estimated the labor cost of a repair job as $336 and he was paid that amount. However, the job took 4 hours longer than he had estimated and, he earned $2 per hour less than his regular hourly rate. What was the time Don had estimated for the job, in hours?
Information given in the question
This is one of those questions which, if approached incorrectly, can be highly time-consuming and increases the probability of doing it wrong.
In this question, it is mentioned that:
We need to find out the originally estimated time to finish the job.
Common approach used by students
This question deals with two separate variables:
Hence, we can write,
Hence, we can write,
Many students get stuck at this point. As they have already replaced the value of xy from the first equation, they feel that they have only one equation with two unknown variables – hence, the question cannot be solved.
If observed closely, one can still solve the equation by replacing the value of either x or y from the 1st equation into this derived equation to get the answer.
From equation 1 we can write:
Observation
Correct Approach and Solution
We can assume the estimated time for Don to complete the job is t hours.
Hence, we can write:
Common mistake type 3: Incorrect interpretation of the question statement
e-GMAT Example 4
A, B, and C, working individually, can complete a job in 10 days, 12 days, and 15 days respectively. All of them started working on the job together. B left after 2 days. C left 2 days before the originally scheduled number of days at which the job was supposed to be completed. In how many days the job completed?
Common approach used by students
In this question, it is given that:
Now, we can assume the total work to be LCM (10, 12, 15) = 60 units
Now, let’s assume the total work gets completed in d days
Hence, we can say
As we know the work done by them individually in 1 day, we can calculate the total work done by them.
Solving, 10d = 58
Or, d = 5.8 days
Hence, the total work gets completed in 5.8 days
If you have got 5.8 days as the answer, then you have solved it incorrectly.
The mistake and the Correct Approach
Here the mistake lies in the wrong interpretation of the question statement.
In the solution we assumed that the total number of days taken to complete the job is d days. From that, it is inferred that the number of days C worked for is (d – 2) days.
However, in the question it was mentioned that C left 2 days before the originally scheduled number of days at which the job was supposed to be completed.
Now, the total work done by all 3 of them together in 1 day = (6 + 5 + 4) units = 15 units
Hence, the original scheduled work completion time = \(\frac{60}{15}\) days = 4 days
Therefore, C worked for (4 – 2) days = 2 days in total
Hence, we can say
Solving, 6d = 42
Or, d = 7 days
The total work gets completed in 7 days’ time
Takeaways from this article
Did you enjoy this article?
If you have enjoyed the article, then try the practice questions given below.
3 Deadly Mistakes You Must Avoid in Time and Work Questions
This is the 2nd and the final article on the topic Time and Work. If you have not read the previous article, we recommend you read that first before going through this article.
To read the article: Solve Time and Work Problems Efficiently using Efficiency Method!
Highlights of the previous article
In the previous article, we discussed:
- The application of LCM to solve Time and Work questions.
A comparative study of methods of solving Time and Work problems – by using fraction and by using LCM method, which one should be used and when?
How efficiency is defined and in what ways it can be implemented in problem solving.
Objective of this article
The primary objective of this article is to cite 3 most common mistakes made by students while solving problems on Time and Work. We will demonstrate them with different examples on each type. For students’ convenience, we have referred to examples similar to what are provided in the official resources.
Common mistake type 1: Incorrect use of the relationship between efficiency and time taken
e-GMAT Example 1
Six machines at a certain factory operate at the same constant rate. If four of these machines, operating simultaneously, take 27 hours to fill a certain production order, how many fewer hours does it take all six machines, operating simultaneously, to fill the same production order?
Common approach used by students
In this question it is given that
- • 4 machines take 27 hours to fill a certain production order
• All machines operate at the same constant rate
Now, it is given that,
- • 4 machines take 27 hours to fill the production order
- • Hence, 1 machine will take \(\frac{27}{4}\) hours to fill the same production order
• Therefore, 6 machines will take \(\frac{27}{4} * 6\) hours = 40.5 hours to fill the production order
If you have got 13.5 hours as the answer, then you have solved it incorrectly.
Let us take another similar example before discussing the mistake and the solution.
e-GMAT Example 2
Six machines, each working at the same constant rate, together can complete a certain job in 12 days. How many additional machines, each working at the same constant rate, will be needed to complete the job in 8 days?
Common approach used by students
In this question, it is given that:
- • 6 machines can complete a certain job in 12 days
• All machines work at the same constant rate
Now it is given that,
- • 6 machines can complete the job in 12 days
- • Hence, 1 machine can complete the job in \(\frac{12}{6}\) days = 2 days
If you have got 4 as the answer, then you have solved it incorrectly.
The mistakes and the correct approach
The error made in both the questions are very similar in nature, and the most common type of error that students make while solving. Let us look into the detail of them:
Error in Question 1
In the first question, when we are calculating the time taken by 1 machine to complete the production order, we have made a logical error.
It is given that all machines operate at the same working rate.
- • Therefore, if 4 machines can fill the production order in 27 hours, logically 1 machine should take 4 times the time taken by 4 machines to fill the same production order.
- • This is happening because the efficiency of 1 individual machine is \(\frac{1}{4}\) times of the combined efficiency of 4 machines.
• Because, efficiency and time taken are inversely proportional to each other, the time taken by 1 machine should be 4 times of the time taken by the 4 machines combined.
Error in Question 2
The solution of this question contains 2 errors.
Error 1: Same as the previous question, if 6 machines can complete the job in 12 days, then 1 machine will be completing it by taking 6 times the original time.
Error 2: Moreover, if 1 machine can complete the job in 2 days, you don’t need 4 machines to complete the job in 8 days – as 1 machine itself can complete it in 2 days’ time.
The Correct Solution – Question 1
Given that,
- • 4 machines can complete the job in 27 hours.
- • Hence, 1 machine will complete the job in 27 * 4 = 108 hours
• Therefore, the total job is of 108 machine-hours.
The Correct Solution – Question 2
Given that,
- • 6 machines can complete a certain job in 12 days
- • Hence, the total job is of 12 * 6 = 72 machine-hours.
Common mistake type 2: The Incorrect Approach
e-GMAT Example 3
At his regular hourly rate, Don had estimated the labor cost of a repair job as $336 and he was paid that amount. However, the job took 4 hours longer than he had estimated and, he earned $2 per hour less than his regular hourly rate. What was the time Don had estimated for the job, in hours?
- A. 28
B. 24
C. 16
D. 14
E. 12
Information given in the question
This is one of those questions which, if approached incorrectly, can be highly time-consuming and increases the probability of doing it wrong.
In this question, it is mentioned that:
- • Don had estimated the labor cost of a repair job as $336, which he was paid
• The job took 4 hours longer than originally estimated
• As a result, Don earned $2 less than his original estimated hourly rate
We need to find out the originally estimated time to finish the job.
Common approach used by students
This question deals with two separate variables:
- • Number of hours estimated to complete the job – assuming it to be x
• The payment per hour of job – assuming it to be y
Hence, we can write,
- • xy = 336 [equation 1]
Hence, we can write,
- • (x + 4) (y – 2) = 336 [equation 2]Simplifying, we get xy – 2x + 4y – 8 = 336
Replacing the value of xy from equation 1, we get 336 – 2x + 4y – 8 = 336
Or, -2x + 4y = 8
Or, 4y – 2x = 8
Or, 2y – x = 4
Many students get stuck at this point. As they have already replaced the value of xy from the first equation, they feel that they have only one equation with two unknown variables – hence, the question cannot be solved.
If observed closely, one can still solve the equation by replacing the value of either x or y from the 1st equation into this derived equation to get the answer.
From equation 1 we can write:
- • \(x = \frac{336}{y}\)
- • \(2y – \frac{336}{y} = 4\)
Or, \(2y^2 – 336 = 4y\)
Or, \(2y^2 – 4y – 336 = 0\)
Or, \(y^2 – 2y – 168 = 0\)
Or, \(y^2 – 14y + 12y – 168 = 0\)
Or, (y – 14) (y + 12) = 0
As y cannot be negative, y = 14
Replacing the value of y in the equation x = \(\frac{336}{y}\) , we get x = 24
Observation
- • Primarily this question does not need the usage of two variables. The question asks for the estimated time required for the job and only this can be assumed as the variable for the solving purpose.
• While solving the values for x and y, the value of y should not be solved. The question asks for x only, therefore, x should be solved on the first attempt.
Correct Approach and Solution
We can assume the estimated time for Don to complete the job is t hours.
- • Therefore, the original estimated earnings per hour = \(\frac{336}{t}\)
• As Don took 4 hours extra, his earnings per hour becomes \(\frac{336}{(t+4)}\)
Hence, we can write:
- • \(\frac{336}{t}\) - \(\frac{336}{(t+4)}\) = 2
Simplifying, we get \(t^2 + 4t – 672 = 0\)
• At this point one can also form equation and solving that to get the answer. However, if solving becomes difficult, one can also replace the options in place of t in the equation \(\frac{336}{t}\) - \(\frac{336}{(t+4)}\) = 2, to get the answer.
Common mistake type 3: Incorrect interpretation of the question statement
e-GMAT Example 4
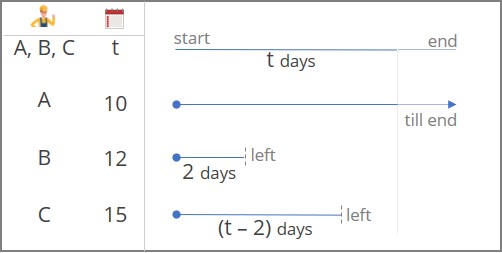
A, B, and C, working individually, can complete a job in 10 days, 12 days, and 15 days respectively. All of them started working on the job together. B left after 2 days. C left 2 days before the originally scheduled number of days at which the job was supposed to be completed. In how many days the job completed?
Common approach used by students
In this question, it is given that:
- • A, B, and C can complete a certain job in 10, 12, and 15 days respectively, while working individually
• All of them started working on the job together
• B left after working for 2 days
• C left 2 days before the originally scheduled work completion time
Now, we can assume the total work to be LCM (10, 12, 15) = 60 units
- • A can complete 60 units of work in 10 days
- o Hence, A can complete 6 units of work in 1 day
- o Hence, B can complete 5 units of work in 1 day
- o Hence, C can complete 4 units of work in 1 day
Now, let’s assume the total work gets completed in d days
Hence, we can say
- • A works for d days
• B works for 2 days
• C works for (d-2) days
As we know the work done by them individually in 1 day, we can calculate the total work done by them.
- • Work done by A = 6 * d units = 6d units
• Work done by B = 5 * 2 units = 10 units
• Work done by C = 4 * (d – 2) units = 4d – 8 units
Solving, 10d = 58
Or, d = 5.8 days
Hence, the total work gets completed in 5.8 days
If you have got 5.8 days as the answer, then you have solved it incorrectly.
The mistake and the Correct Approach
Here the mistake lies in the wrong interpretation of the question statement.
In the solution we assumed that the total number of days taken to complete the job is d days. From that, it is inferred that the number of days C worked for is (d – 2) days.
However, in the question it was mentioned that C left 2 days before the originally scheduled number of days at which the job was supposed to be completed.
- • One need to notice that d days doesn’t indicate the originally scheduled work completion time, rather it indicates the modified work completion time
• The originally scheduled work completion time indicates the time in which the work would have been completed if all A, B, and C worked together till last
Now, the total work done by all 3 of them together in 1 day = (6 + 5 + 4) units = 15 units
Hence, the original scheduled work completion time = \(\frac{60}{15}\) days = 4 days
Therefore, C worked for (4 – 2) days = 2 days in total
Hence, we can say
- • Work done by A = 6 * d units = 6d units
• Work done by B = 5 * 2 units = 10 units
• Work done by C = 4 * 2 units = 8 units
Solving, 6d = 42
Or, d = 7 days
The total work gets completed in 7 days’ time
Takeaways from this article
- • For any person or machine, efficiency and work rate are always inversely proportional to each other. Hence, less number of resources working on a specific job always take more time compared to more number of resources working on the same job
• While solving, one needs to focus on the exact parameter which the question is asking for. Sometimes assuming more than what required can complicate the calculation and increases the chance of making error.
• While making inferences from the question stem, one needs to decipher the correct meaning of the given statements, and ensure the details are considered while solving – ignoring which may lead into wrong interpretation and incorrect answer.
Did you enjoy this article?
If you have enjoyed the article, then try the practice questions given below.
Attachments
![]() 3 mistakes Time and work.pdf [593.81 KiB]
3 mistakes Time and work.pdf [593.81 KiB]
Downloaded 349 times
Originally posted by EgmatQuantExpert on 30 May 2018, 03:41.
Last edited by EgmatQuantExpert on 13 Aug 2018, 00:12, edited 1 time in total.
Last edited by EgmatQuantExpert on 13 Aug 2018, 00:12, edited 1 time in total.
Kudos
Bookmarks
Here is a list of questions specifically designed to help you apply the learnings from this article.
Exercise Questions
Question 1
Question 2
Question 3
Question 4
Detailed solutions will be posted soon.
Happy Learning!
Exercise Questions
Question 1
Question 2
Question 3
Question 4
Detailed solutions will be posted soon.
Happy Learning!
Kudos
Bookmarks
Hey everyone,
The official answers to all the practice questions have been posted.
Regards,
Tamal
e-GMAT
The official answers to all the practice questions have been posted.
Regards,
Tamal
e-GMAT