Peddi wrote:
chetan2u wrote:
soumya170293 wrote:
A rectangle ABCD is to be constructed on the XY plane so that AB is || to the y axis ; if the X and Y co-ordinates of A,B,C & D are integers between -3 to 6 ; How many different rectangles can be constructed ?
A > 81
B > 100
C > 2025
D > 10000
E > 12100
So we have X and Y ranging from -3 to 6 that is 10 by 10 integer values.
You can choose 2 points in X coordinates in 10C2 ways, and for each of this way, we can choose 2 points in y coordinates in 10C2 ways.
Thus total ways = 10C2*10C2=45*45=2025
C
I didnt understand your approach , can you elaborate
Posted from my mobile deviceTried as concise an explanation as it can be but this is best i can offer. You have to be a little patient.

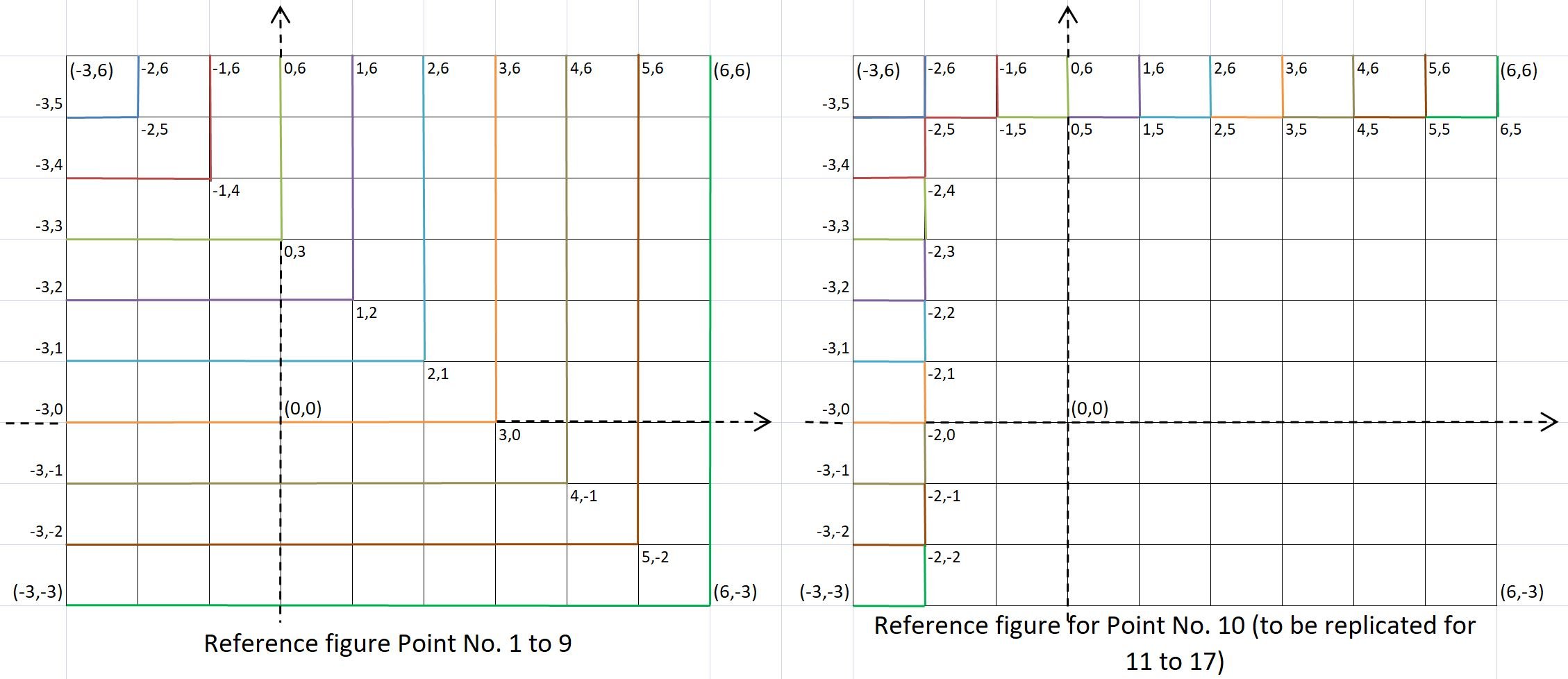
The coordinates within which these rectangles can be formed are (-3,6) (6,6) (6,-3) (-3,-3).
From Point no. 1 to 9 = 81 + 64 + 49 + 36 + 25 + 16 + 9 + 4 + 1 = 285
From Point No. 10 to 17 = 2 * (72 + 63 + 54 + 45 + 36 + 27 + 18 + 9) = 648
From Point No. 18 to 24 = 2 * (56 + 48 + 40 + 32 + 24 + 16 + 8) = 448
From Point No. 25 to 30 = 2 * (42 + 35 + 28 + 21 + 14 + 7) = 294
From Point No. 31 to 35 = 2 * (30 + 24 + 18 + 12 + 6) = 180
From Point No. 36 to 39 = 2 * (20 + 15 + 10 + 5) = 100
From Point No. 40 to 42 = 2 * (12 + 8 + 4) = 48
From Point No. 43 to 44 = 2 * (6 + 3) = 18
From Point No. 45 = 2 * (2) = 4
Total formations are = 285 + 648 + 448 + 294 + 180 + 100 + 48 + 18 + 4 = 2025.
Explanation as below: (refer figure)
Attachment:
File comment: Rectangle ABCD
 Rectangle .JPG [ 201.35 KiB | Viewed 6508 times ]
Rectangle .JPG [ 201.35 KiB | Viewed 6508 times ]
So, we can take rectangles(including squares) with dimensions as follows:
1.
1Hx1V (sides with two consecutive coordinates for example (-3,6) (-2,6) (-2,5) (-3,5) and so on). Total formations = 9 x 9 = 81
2.
2Hx2V (sides with two coordinates having 1 coordinate in between for example (-3,6) (-1,6) (-1,4) (-3,4) and so on) Total formations = 8*8 = 64
3.
3Hx3V (sides with two coordinates having 2 coordinates in between for example (-3,6) (0,6) (0,3) (-3,3) and so on) Total formations = 7*7 = 49
4.
4Hx4V (sides with two coordinates having 3 coordinates in between for example (-3,6) (1,6) (1,2) (-3,2) and so on) Total formations = 6*6 = 36
5.
5Hx5V (sides with two coordinates having 4 coordinates in between for example (-3,6) (2,6) (2,1) (-3,1) and so on) Total formations = 5*5 = 25
6.
6Hx6V (sides with two coordinates having 5 coordinates in between for example (-3,6) (3,6) (3,0) (-3,0) and so on) Total formations = 4*4 = 16
7.
7Hx7V (sides with two coordinates having 6 coordinates in between for example (-3,6) (4,6) (4,-1) (-3,-1) and so on) Total formations = 3*3 = 9
8.
8Hx8V (sides with two coordinates having 7 coordinates in between for example (-3,6) (5,6) (5,-2) (-3,-2) and so on) Total formations = 2*2 = 4
9.
9Hx9V (sides with two coordinates having 8 coordinates in between for example (-3,6) (6,6) (6,-3) (-3,-3) and so on) Total formations = 1*1 = 1
(where H and V are just for horizontal and vertical reference of side dimensions)
Up till now all formations were of square form.
Other rectangles are: (refer figure)
10.
1Vx2H (sides with two coordinates having 0 coordinates and having 1 coordinate along y-axis and x-axis respectively in between for example (-3,6) (-1,6) (-1,5) (-3,5) and so on) Total formations = 9 x 8 = 72
11.
1Vx3H (sides with two coordinates having 0 coordinates and having 2 coordinates along y-axis and x-axis respectively in between for example (-3,6) (0,6) (0,5) (-3,5) and so on) Total formations = 9 x 7 = 63
12.
1Vx4H (sides with two coordinates having 0 coordinates and having 3 coordinates along y-axis and x-axis respectively in between for example (-3,6) (1,6) (1,5) (-3,5) and so on) Total formations = 9 x 6 = 54
13.
1Vx5H (sides with two coordinates having 0 coordinates and having 4 coordinates along y-axis and x-axis respectively in between for example (-3,6) (2,6) (2,5) (-3,5) and so on) Total formations = 9 x 5 = 45
14.
1Vx6H (sides with two coordinates having 0 coordinates and having 5 coordinates along y-axis and x-axis respectively in between for example (-3,6) (3,6) (3,5) (-3,5) and so on) Total formations = 9 x 4 = 36
15.
1Vx7H (sides with two coordinates having 0 coordinates and having 6 coordinates along y-axis and x-axis respectively in between for example (-3,6) (4,6) (4,5) (-3,5) and so on) Total formations = 9 x 3 = 27
16.
1Vx8H (sides with two coordinates having 0 coordinates and having 7 coordinates along y-axis and x-axis respectively in between for example (-3,6) (5,6) (5,5) (-3,5) and so on) Total formations = 9 x 2 = 18
17.
1Vx9H (sides with two coordinates having 0 coordinates and having 8 coordinates along y-axis and x-axis respectively in between for example (-3,6) (6,6) (6,5) (-3,5) and so on) Total formations = 9 x 1 = 9
18. 2Vx3H (sides with two coordinates having 1 coordinate and 2 coordinates along y-axis and x-axis respectively in between for example (-3,6) (0,6) (0,4) (-3,4) and so on) Total formations = 8 x 7 = 56
19. 2Vx4H (sides with two coordinates having 1 coordinate and 3 coordinates along y-axis and x-axis respectively in between for example (-3,6) (1,6) (1,4) (-3,4) and so on) Total formations = 8 x 6 = 48
20. 2Vx5H (sides with two coordinates having 1 coordinate and 4 coordinates along y-axis and x-axis respectively in between for example (-3,6) (2,6) (2,4) (-3,4) and so on) Total formations = 8 x 5 = 40
21. 2Vx6H (sides with two coordinates having 1 coordinate and 5 coordinates along y-axis and x-axis respectively in between for example (-3,6) (3,6) (3,4) (-3,4) and so on) Total formations = 8 x 4 = 32
22. 2Vx7H (sides with two coordinates having 1 coordinate and 6 coordinates along y-axis and x-axis respectively in between for example (-3,6) (4,6) (4,4) (-3,4) and so on) Total formations = 8 x 3 = 24
23. 2Vx8H (sides with two coordinates having 1 coordinate and 7 coordinates along y-axis and x-axis respectively in between for example (-3,6) (5,6) (5,4) (-3,4) and so on) Total formations = 8 x 2 = 16
24. 2Vx9H (sides with two coordinates having 1 coordinate and 8 coordinates along y-axis and x-axis respectively in between for example (-3,6) (6,6) (6,4) (-3,4) and so on) Total formations = 8 x 1 = 8
Again
25. 3Vx4H (sides with two coordinates having 2 coordinate and 3 coordinates along y-axis and x-axis respectively in between for example (-3,6) (1,6) (1,3) (-3,3) and so on) Total formations = 7 x 6 = 42
26. 3Vx5H (sides with two coordinates having 2 coordinate and 4 coordinates along y-axis and x-axis respectively in between for example (-3,6) (2,6) (2,3) (-3,3) and so on) Total formations = 7 x 5 = 35
27. 3Vx6H (sides with two coordinates having 2 coordinate and 5 coordinates along y-axis and x-axis respectively in between for example (-3,6) (3,6) (3,3) (-3,3) and so on) Total formations = 7 x 4 = 28
28. 3Vx7H (sides with two coordinates having 2 coordinate and 6 coordinates along y-axis and x-axis respectively in between for example (-3,6) (4,6) (4,3) (-3,3) and so on) Total formations = 7 x 3 = 21
29. 3Vx8H (sides with two coordinates having 2 coordinate and 4 coordinates along y-axis and x-axis respectively in between for example (-3,6) (5,6) (5,3) (-3,3) and so on) Total formations = 7 x 2 = 14
30. 3Vx9H (sides with two coordinates having 2 coordinate and 8 coordinates along y-axis and x-axis respectively in between for example (-3,6) (2,6) (2,3) (-3,3) and so on) Total formations = 7 x 1 = 7
31. 4Vx5H (sides with two coordinates having 3 coordinate and 4 coordinates along y-axis and x-axis respectively in between for example (-3,6) (2,6) (2,2) (-3,2) and so on) Total formations = 6 x 5 = 30
32. 4Vx6H (sides with two coordinates having 3 coordinate and 5 coordinates along y-axis and x-axis respectively in between for example (-3,6) (3,6) (3,2) (-3,2) and so on) Total formations = 6 x 4 = 24
33. 4Vx7H (sides with two coordinates having 3 coordinate and 6 coordinates along y-axis and x-axis respectively in between for example (-3,6) (4,6) (4,2) (-3,2) and so on) Total formations = 6 x 3 = 18
34. 4Vx8H (sides with two coordinates having 3 coordinate and 7 coordinates along y-axis and x-axis respectively in between for example (-3,6) (5,6) (5,2) (-3,2) and so on) Total formations = 6 x 2 = 12
35. 4Vx9H (sides with two coordinates having 3 coordinate and 4 coordinates along y-axis and x-axis respectively in between for example (-3,6) (6,6) (6,2) (-3,2) and so on) Total formations = 6 x 1 = 6
36. 5Vx6H (sides with two coordinates having 4 coordinate and 5 coordinates along y-axis and x-axis respectively in between for example (-3,6) (3,6) (3,1) (-3,1) and so on) Total formations = 5 x 4 = 20
37. 5Vx7H (sides with two coordinates having 4 coordinate and 6 coordinates along y-axis and x-axis respectively in between for example (-3,6) (4,6) (4,1) (-3,1) and so on) Total formations = 5 x 3 = 15
38. 5Vx8H (sides with two coordinates having 4 coordinate and 7 coordinates along y-axis and x-axis respectively in between for example (-3,6) (5,6) (5,1) (-3,1) and so on) Total formations = 5 x 2 = 10
39. 5Vx9H (sides with two coordinates having 4 coordinate and 8 coordinates along y-axis and x-axis respectively in between for example (-3,6) (6,6) (6,1) (-3,1) and so on) Total formations = 5 x 1 = 5
40. 6Vx7H (sides with two coordinates having 5 coordinate and 6 coordinates along y-axis and x-axis respectively in between for example (-3,6) (4,6) (4,0) (-3,0) and so on) Total formations = 4 x 3 = 12
41. 6Vx8H (sides with two coordinates having 5 coordinate and 7 coordinates along y-axis and x-axis respectively in between for example (-3,6) (5,6) (5,0) (-3,0) and so on) Total formations = 4 x 2 = 8
42. 6Vx9H (sides with two coordinates having 5 coordinate and 8 coordinates along y-axis and x-axis respectively in between for example (-3,6) (6,6) (6,0) (-3,0) and so on) Total formations = 4 x 1 = 4
43. 7Vx8H (sides with two coordinates having 6 coordinate and 7 coordinates along y-axis and x-axis respectively in between for example (-3,6) (5,6) (5,-1) (-3,-1) and so on) Total formations = 3 x 2 = 6
44. 7Vx9H (sides with two coordinates having 6 coordinate and 8 coordinates along y-axis and x-axis respectively in between for example (-3,6) (6,6) (6,-1) (-3,-1) and so on) Total formations = 3 x 1 = 3
45. 8Vx9H (sides with two coordinates having 7 coordinate and 8 coordinates along y-axis and x-axis respectively in between for example (-3,6) (5,6) (6,0) (-3,0) and so on) Total formations = 2 x 1 = 2
Since point no. 10 to 45 will have a mirror image along the diagonal (-3,6) – (6,-3), the number of each formations calculated above for point no. 10 to 45 would be doubled.
Example: For Point No. 10, 1Vx2H (sides with two coordinates having 0 coordinates and having 1 coordinate along y-axis and x-axis respectively in between for example (-3,6) (-1,6) (-1,5) (-3,5)) would have an exact replica as 2Vx1H (sides with two coordinates having 0 coordinates and having 1 coordinate along y-axis and x-axis respectively in between for example (-3,6) (-2,6) (-2,4) (-3,4)) and so on). Then Total formations would be = 2 x 9 x 8 = 144 and so on…
gvij2017 Have a look. Since side of rectangle is always || to an axis, only these are possible formations.
Hope this is helpful.
_________________
Pain + Reflection = Progress | Ray Dalio
Good Books to read prior to MBA




 85%
(hard)
85%
(hard)
 47%
(02:48)
wrong
47%
(02:48)
wrong  based on 286
sessions
based on 286
sessions




![]() A rectangle ABCD is to be constructed on the XY plane so that AB is.docx [15.83 KiB]
A rectangle ABCD is to be constructed on the XY plane so that AB is.docx [15.83 KiB]
