Last visit was: 19 Nov 2025, 03:43 It is currently 19 Nov 2025, 03:43
Home
GMAT
Messages
Tests
Schools
Events
Rewards
Chat
My Profile
Close
GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.

Customized
for You

we will pick new questions that match your level based on your Timer History

Track
Your Progress

every week, we’ll send you an estimated GMAT score based on your performance

Practice
Pays

we will pick new questions that match your level based on your Timer History
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Go to My Error Log Learn more
Close
Request Expert Reply
Confirm Cancel
Back to Forum
Create Topic
   1   2   3 
Theory|   
avatar
akankshasbisen
avatar
Joined: 20 Feb 2016
Last visit: 19 Nov 2019
Posts: 3
Own Kudos:
2
Given Kudos: 11
Posts: 3
Kudos: 2
Math: Circles 19 Jun 2016, 09:10
Kudos
Add Kudos
Bookmarks
Bookmark this Post
Very helpful. It helped clear a lot of my concepts on circles.
User avatar
goforgmat
User avatar
Joined: 09 Feb 2015
Last visit: 02 Nov 2019
Posts: 246
Own Kudos:
107
Given Kudos: 232
Location: India
Concentration: Social Entrepreneurship, General Management
Schools: Booth '21 (D) Cambridge "21 (D) LBS '22 (D)
GMAT 1: 690 Q49 V34
GMAT 2: 720 Q49 V39
GPA: 2.8
Products:
My Reviews
Schools: Booth '21 (D) Cambridge "21 (D) LBS '22 (D)
GMAT 2: 720 Q49 V39
Posts: 246
Kudos: 107
Math: Circles 17 Aug 2017, 13:36
Kudos
Add Kudos
Bookmarks
Bookmark this Post
Bunuel
I have a doubt here . Consider the last figure! If the lines OA and OB are drawn, what will be the resulting Angle OAP and OBP ?
avatar
Shokhrukh22
avatar
Joined: 04 Jan 2016
Last visit: 23 Sep 2020
Posts: 4
Own Kudos:
27
Given Kudos: 8
Location: Uzbekistan
GMAT 1: 680 Q49 V33
GPA: 3.72
WE:Analyst (Consulting)
GMAT 1: 680 Q49 V33
Posts: 4
Kudos: 27
Math: Circles 01 Mar 2019, 02:37
Kudos
Add Kudos
Bookmarks
Bookmark this Post
Thank you! Vey useful formulas. Are The Central Angle Theorem and Power of a Point Theorem tested on GMAT? Are test takers expected to know these theorems and formulas? I have solved Official guides 2018, but did not see any problem that required the knowledge of these theorems. In OG 2018 Quantitative review problem #216, they gave the formula in the problem itself. I am taking my GMAT this month, but i am not sure whether i should master these formulas & theorems, or it is better to focus on what is given in math review part of the OG books.
User avatar
pratik2018
User avatar
Joined: 09 Apr 2017
Last visit: 23 Jun 2020
Posts: 37
Own Kudos:
186
Given Kudos: 188
Location: Nepal
Concentration: Finance, Entrepreneurship
Schools: Johnson '22 (S)
GMAT 1: 580 Q47 V22
GMAT 2: 640 Q48 V29
GMAT 3: 690 Q48 V36
WE:Information Technology (Computer Software)
Products:
My Reviews
Schools: Johnson '22 (S)
GMAT 3: 690 Q48 V36
Posts: 37
Kudos: 186
Math: Circles 09 Aug 2019, 02:05
Kudos
Add Kudos
Bookmarks
Bookmark this Post
This is the best material ever to be found related to GMAT quants.
User avatar
loki14
User avatar
Joined: 18 Feb 2020
Last visit: 17 Nov 2023
Posts: 26
Own Kudos:
7
 [1]
Given Kudos: 98
Location: India
Concentration: Strategy, Operations
Schools: ISB '23 (II)
GMAT 1: 700 Q49 V36
Schools: ISB '23 (II)
GMAT 1: 700 Q49 V36
Posts: 26
Kudos: 7
 [1]
Math: Circles 23 Apr 2021, 07:15
1
Kudos
Add Kudos
Bookmarks
Bookmark this Post
Bunuel
chauhan2011
• If you know the length of the minor arc and radius, the inscribed angle is: 90L/nr

Please correct me if i am wrong but i think the formula should be : 180L/nr

If you know the length \(L\) of the minor arc and radius, the inscribed angle is: \(Inscribed \ Angle=\frac{90L}{\pi{r}}\).

The way to derive the above formula:

Length of minor arc is \(L= \frac{Central \ Angle}{360}* Circumference\) --> \(L= \frac{Central \ Angle}{360}* 2\pi{r}\) --> \(L= \frac{Central \ Angle}{180}* 2\pi{r}\) --> \(Central \ Angle=\frac{180L}{\pi{r}}\) (so maybe you've mistaken central angle for inscribed angle?).

The Central Angle Theorem states that the measure of inscribed angle is always half the measure of the central angle: \(Central \ Angle=2*Inscribed \ Angle\).

So, \(2*Inscribed \ Angle=\frac{180L}{\pi{r}}\) --> \(Inscribed \ Angle=\frac{90L}{\pi{r}}\).

Hope it helps.
Show more

must be L=(Central Angle/180)∗πr
User avatar
Bunuel
User avatar
Math Expert
Joined: 02 Sep 2009
Last visit: 19 Nov 2025
Posts: 105,379
Own Kudos:
778,193
Given Kudos: 99,977
Products:
GMAT Club Tests Forum Quiz
Expert
Expert reply
Active GMAT Club Expert! Tag them with @ followed by their username for a faster response.
Posts: 105,379
Kudos: 778,193
Math: Circles 23 Apr 2021, 07:59
Kudos
Add Kudos
Bookmarks
Bookmark this Post
Lokeshchinni14
Bunuel
chauhan2011
• If you know the length of the minor arc and radius, the inscribed angle is: 90L/nr

Please correct me if i am wrong but i think the formula should be : 180L/nr

If you know the length \(L\) of the minor arc and radius, the inscribed angle is: \(Inscribed \ Angle=\frac{90L}{\pi{r}}\).

The way to derive the above formula:

Length of minor arc is \(L= \frac{Central \ Angle}{360}* Circumference\) --> \(L= \frac{Central \ Angle}{360}* 2\pi{r}\) --> \(L= \frac{Central \ Angle}{180}* 2\pi{r}\) --> \(Central \ Angle=\frac{180L}{\pi{r}}\) (so maybe you've mistaken central angle for inscribed angle?).

The Central Angle Theorem states that the measure of inscribed angle is always half the measure of the central angle: \(Central \ Angle=2*Inscribed \ Angle\).

So, \(2*Inscribed \ Angle=\frac{180L}{\pi{r}}\) --> \(Inscribed \ Angle=\frac{90L}{\pi{r}}\).

Hope it helps.

must be L=(Central Angle/180)∗πr
Show more

_________________________
Edited the typo. Thank you!
User avatar
SDW2
User avatar
Joined: 17 Jun 2020
Last visit: 05 Mar 2024
Posts: 102
Own Kudos:
11
Given Kudos: 314
Location: India
Schools: Simon '25
Schools: Simon '25
Posts: 102
Kudos: 11
Math: Circles 13 Oct 2022, 07:20
Kudos
Add Kudos
Bookmarks
Bookmark this Post
Bunuel
CIRCLES

This post is a part of [GMAT MATH BOOK]

created by: Bunuel
edited by: bb, walker

--------------------------------------------------------
Get The Official GMAT Club's App - GMAT TOOLKIT 2.
The only app you need to get 700+ score!

[iOS App] [Android App]

--------------------------------------------------------

Definition

A line forming a closed loop, every point on which is a fixed distance from a center point. Circle could also be defined as the set of all points equidistant from the center.




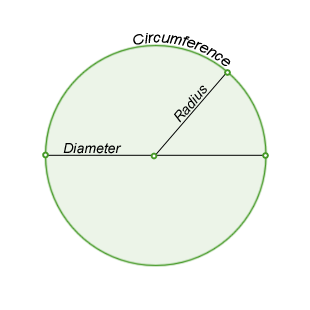Center -a point inside the circle. All points on the circle are equidistant (same distance) from the center point.

Radius - the distance from the center to any point on the circle. It is half the diameter.

Diameter -t he distance across the circle. The length of any chord passing through the center. It is twice the radius.

Circumference - the distance around the circle.

Area - strictly speaking a circle is a line, and so has no area. What is usually meant is the area of the region enclosed by the circle.

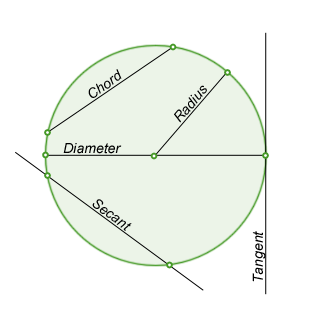
Chord - line segment linking any two points on a circle.

Tangent -a line passing a circle and touching it at just one point.
The tangent line is always at the 90 degree angle (perpendicular) to the radius of a circle.

Secant A line that intersects a circle at two points.

\(\pi\) In any circle, if you divide the circumference (distance around the circle) by it's diameter (distance across the circle), you always get the same number. This number is called Pi and is approximately 3.142.




• A circle is the shape with the largest area for a given length of perimeter (has the highest area to length ratio when compared to other geometric figures such as triangles or rectangles)
• All circles are similar
• To form a unique circle, it needs to have 3 points which are not on the same line.

Circumference, Perimeter of a circle

Given a radius \(r\) of a circle, the circumference can be calculated using the formula: \(Circumference=2\pi{r}\)

If you know the diameter \(D\) of a circle, the circumference can be found using the formula: \(Circumference=\pi{D}\)

If you know the area \(A\) of a circle, the circumference can be found using the formula: \(Circumference=\sqrt{4\pi{A}}\)


Area enclosed by a circle

Given the radius \(r\) of a circle, the area can be calculated using the formula: \(Area={\pi}r^2\)

If you know the diameter \(D\) of a circle, the area can be found using the formula: \(Area=\frac{{\pi}D^2}{4}\)

If you know the circumference \(C\) of a circle, the area can be found using the formula: \(Area=\frac{C^2}{4{\pi}}\)


Semicircle

Half a circle. A closed shape consisting of half a circle and a diameter of that circle.




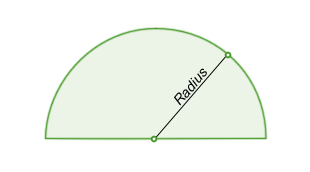
• The area of a semicircle is half the area of the circle from which it is made: \(Area=\frac{{\pi}r^2}{2}\)

• The perimeter of a semicircle is not half the perimeter of a circle. From the figure above, you can see that the perimeter is the curved part, which is half the circle, plus the diameter line across the bottom. So, the formula for the perimeter of a semicircle is: \(Perimeter=\pi{r}+2r=r(\pi+2)\)

• The angle inscribed in a semicircle is always 90°.

• Any diameter of a circle subtends a right angle to any point on the circle. No matter where the point is, the triangle formed with diameter is always a right triangle.



Chord


A line that links two points on a circle or curve.




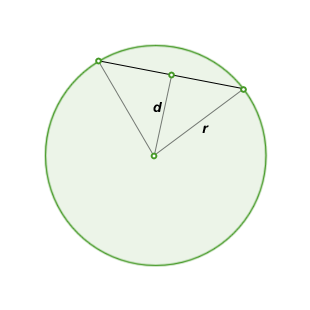
• A diameter is a chord that contains the center of the circle.
• Below is a formula for the length of a chord if you know the radius and the perpendicular distance from the chord to the circle center. This is a simple application of Pythagoras' Theorem.
\(Length=2\sqrt{r^2-d^2}\), where \(r\) is the radius of the circle, \(d\) is the perpendicular distance from the chord to the circle center.
• In a circle, a radius perpendicular to a chord bisects the chord. Converse: In a circle, a radius that bisects a chord is perpendicular to the chord, or In a circle, the perpendicular bisector of a chord passes through the center of the circle.


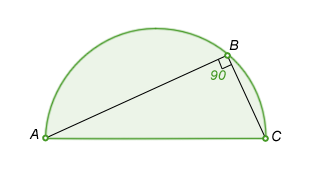
Angles in a circle

An inscribed angle is an angle ABC formed by points A, B, and C on the circle's circumference.




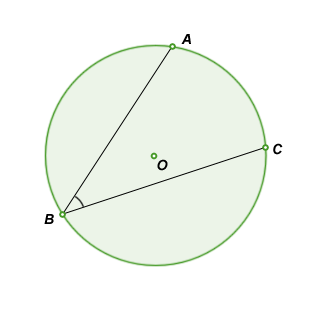
• Given two points A and C, lines from them to a third point B form the inscribed angle ∠ABC. Notice that the inscribed angle is constant. It only depends on the position of A and C.
• If you know the length \(L\) of the minor arc and radius, the inscribed angle is: \(Angle=\frac{90L}{\pi{r}}\)

A central angle is an angle AOC with endpoints A and C located on a circle's circumference and vertex O located at the circle's center. A central angle in a circle determines an arc AC.




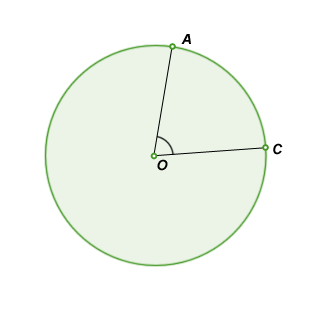
• The Central Angle Theorem states that the measure of inscribed angle is always half the measure of the central angle.




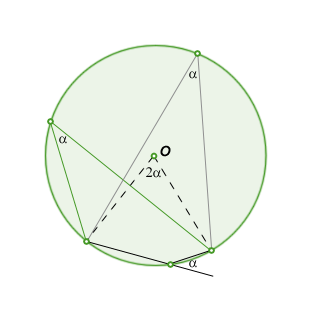
• An inscribed angle is exactly half the corresponding central angle. Hence, all inscribed angles that subtend the same arc are equal. Angles inscribed on the arc are supplementary. In particular, every inscribed angle that subtends a diameter is a right angle (since the central angle is 180 degrees).


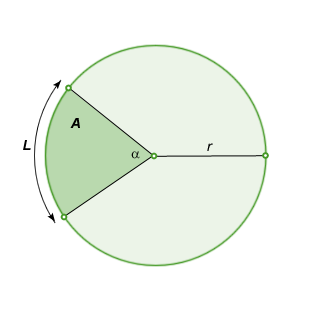
Arcs and Sectors

A portion of the circumference of a circle.




• Major and Minor Arcs Given two points on a circle, the minor arc is the shortest arc linking them. The major arc is the longest. On the GMAT, we usually assume the minor (shortest) arc.

• Arc Length The formula the arc measure is: \(L=2\pi{r}\frac{C}{360}\), where C is the central angle of the arc in degrees. Recall that \(2\pi{r}\) is the circumference of the whole circle, so the formula simply reduces this by the ratio of the arc angle to a full angle (360). By transposing the above formula, you solve for the radius, central angle, or arc length if you know any two of them.

• Sector is the area enclosed by two radii of a circle and their intercepted arc. A pie-shaped part of a circle.

• Area of a sector is given by the formula: \(Area=\pi{r^2}\frac{C}{360}\), where: C is the central angle in degrees. What this formula is doing is taking the area of the whole circle, and then taking a fraction of that depending on the central angle of the sector. So for example, if the central angle was 90°, then the sector would have an area equal to one quarter of the whole circle.


Power of a Point Theorem

Given circle O, point P not on the circle, and a line through P intersecting the circle in two points. The product of the length from P to the first point of intersection and the length from P to the second point of intersection is constant for any choice of a line through P that intersects the circle. This constant is called the "power of point P".

If P is outside the circle: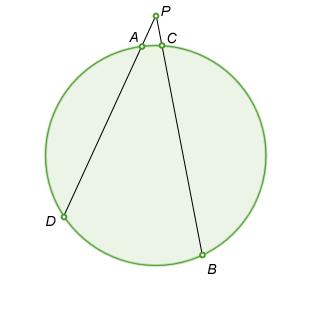




\(PA*PD=PC*PB=Constant\) - This becomes the theorem we know as the theorem of intersecting secants.

If P is inside the circle: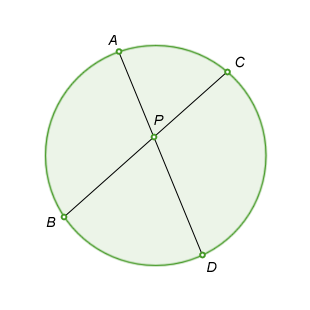




\(PA*PD=PC*PB=Constant\) - This becomes the theorem we know as the theorem of intersecting chords.

Tangent-Secant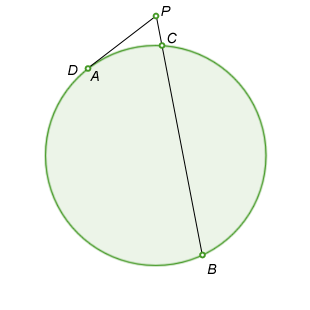




Should one of the lines be tangent to the circle, point A will coincide with point D, and the theorem still applies:

\(PA*PD=PC*PB=Constant\)

\(PA^2=PC*PB=Constant\) - This becomes the theorem we know as the theorem of secant-tangent theorem.

Two tangents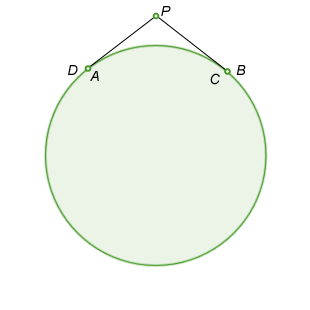




Should both of the lines be tangents to the circle, point A coincides with point D, point C coincides with point B, and the theorem still applies:

\(PA*PD=PC*PB=Constant\)

\(PA^2=PC^2\)

\(PA=PC\)


Official GMAC Books:

The Official Guide, 12th Edition: DT #36; PS #33; PS #160; PS #197; PS #212; DS #42; DS #96; DS #114; DS #117; DS #160; DS #173;
The Official Guide, Quantitative 2th Edition: PS #33; PS #141; PS #145; PS #153; PS #162; DS #22; DS #58; DS #59; DS #95; DS #99;
The Official Guide, 11th Edition: DT #36; PS #30; PS #42; PS #100; PS #160; PS #206; PS #229; DS #23; DS #76; DS #86; DS #136; DS #152;

Generated from [GMAT ToolKit]

--------------------------------------------------------
Get The Official GMAT Club's App - GMAT TOOLKIT 2.
The only app you need to get 700+ score!

[iOS App] [Android App]

--------------------------------------------------------


Show SpoilerImages
Attachment:
Math_cir_3.png
Attachment:
Math_cir_13.png
Attachment:
Math_cir_12.png
Attachment:
Math_cir_10.png
Attachment:
Math_cir_9.png
Attachment:
Math_cir_8.png
Attachment:
Math_cir_7.png
Attachment:
Math_cir_6.png
Attachment:
Math_cir_5.png
Attachment:
Math_cir_4.png
Attachment:
Math_cir_2.png
Attachment:
Math_cir_1.png
Attachment:
Math_icon_circles.png
Attachment:
Math_cir_11.png
Show more


Hi Bunuel,
In the diagram below the central angle theorem, I see that the angle a (by "a" I mean alpha because I can't type it), should be inscribed the same arc as central angle but of the 3 angle a, one seem to be outside (the one alpha below the central angle as shown in the diagram). How is it that it is angle a(alpha) and not its adjacent one? Because the adjacent one seems to be angle a (alpha).
Please provide clarity
User avatar
bumpbot
User avatar
Non-Human User
Joined: 09 Sep 2013
Last visit: 04 Jan 2021
Posts: 38,582
Own Kudos:
1,079
Posts: 38,582
Kudos: 1,079
Math: Circles 24 Nov 2024, 10:59
Kudos
Add Kudos
Bookmarks
Bookmark this Post
Hello from the GMAT Club BumpBot!

Thanks to another GMAT Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).

Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.
   1   2   3 
Moderator:
Bunuel
Math Expert
105379 posts