Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
POLYGONS
created by: Bunuel
edited by: bb, walker
--------------------------------------------------------
This post is a part of [GMAT MATH BOOK]
--------------------------------------------------------
Get The Official GMAT Club's App - GMAT TOOLKIT 2.
The only app you need to get 700+ score!
[iOS App] [Android App]
--------------------------------------------------------
Types of Polygon
Regular A polygon with all sides and interior angles the same. Regular polygons are always convex.
Convex All interior angles less than 180°, and all vertices 'point outwards' away from the interior. The opposite of concave. Regular polygons are always convex.
Definitions, Properties and Tips
• Sum of Interior Angles \(180(n-2)\) where \(n\) is the number of sides
• For a regular polygon, the total described above is spread evenly among all the interior angles, since they all have the same values. So for example the interior angles of a pentagon always add up to 540°, so in a regular pentagon (5 sides), each one is one fifth of that, or 108°. Or, as a formula, each interior angle of a regular polygon is given by: \(\frac{180(n-2)}{n}\), where \(n\) is the number of sides.
• The apothem of a polygon is a line from the center to the midpoint of a side. This is also the inradius - the radius of the incircle. 
polyincircle.gif [ 2.68 KiB | Viewed 160880 times ]
• The radius of a regular polygon is a line from the center to any vertex. It is also the radius of the circumcircle of the polygon. 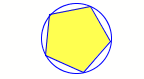
polycircumcircle.gif [ 2.91 KiB | Viewed 160774 times ]
GMAT is dealing mainly with the following polygons:
Quadrilateral A polygon with four 'sides' or edges and four vertices or corners. 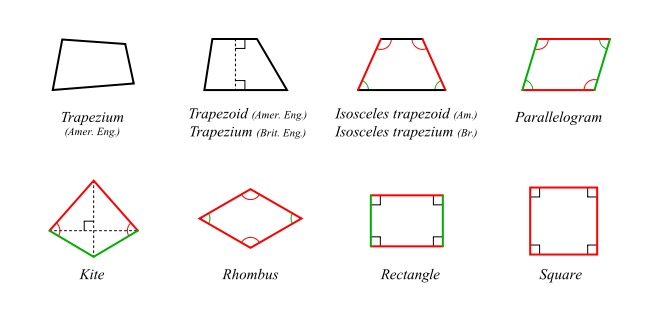
661px-Quadrilaterals.svg.png [ 24.04 KiB | Viewed 163704 times ]
Types of quadrilateral:
Square All sides equal, all angles 90°. See Definition of a square.
Rectangle Opposite sides equal, all angles 90°. See Definition of a rectangle.
Parallelogram Opposite sides parallel. See Definition of a parallelogram.
Trapezoid Two sides parallel. See Definition of a trapezoid.
Rhombus Opposite sides parallel and equal. See Definition of a rhombus.
Parallelogram A quadrilateral with two pairs of parallel sides. 
255px-Parallelogram.svg.png [ 6.3 KiB | Viewed 169406 times ]
Properties and Tips
• Opposite sides of a parallelogram are equal in length.
• Opposite angles of a parallelogram are equal in measure.
• Opposite sides of a parallelogram will never intersect.
• The diagonals of a parallelogram bisect each other.
• Consecutive angles are supplementary, add to 180°.
• The area, \(A\), of a parallelogram is \(A = bh\), where \(b\) is the base of the parallelogram and \(h\) is its height.
• The area of a parallelogram is twice the area of a triangle created by one of its diagonals.
A parallelogram is a quadrilateral with opposite sides parallel and congruent. It is the "parent" of some other quadrilaterals, which are obtained by adding restrictions of various kinds:
• A rectangle is a parallelogram but with all angles fixed at 90°
• A rhombus is a parallelogram but with all sides equal in length
• A square is a parallelogram but with all sides equal in length and all angles fixed at 90°
Rectangle A 4-sided polygon where all interior angles are 90° 
250px-Rectangle_.png [ 752 Bytes | Viewed 160339 times ]
Properties and Tips
• Opposite sides are parallel and congruent
• The diagonals bisect each other
• The diagonals are congruent
• A square is a special case of a rectangle where all four sides are the same length.
• It is also a special case of a parallelogram but with extra limitation that the angles are fixed at 90°.
• The two diagonals are congruent (same length).
• Each diagonal bisects the other. In other words, the point where the diagonals intersect (cross), divides each diagonal into two equal parts.
• Each diagonal divides the rectangle into two congruent right triangles. Because the triangles are congruent, they have the same area, and each triangle has half the area of the rectangle.
• \(Diagonal=\sqrt{w^2+h^2}\) where: \(w\) is the width of the rectangle, h is the height of the rectangle.
• The area of a rectangle is given by the formula \(Width*Height\).
A rectangle can be thought about in other ways:
• A square is a special case of a rectangle where all four sides are the same length. Adjust the rectangle above to create a square.
• It is also a special case of a parallelogram but with extra limitation that the angles are fixed at 90°.
Squares A 4-sided regular polygon with all sides equal and all internal angles 90° 
220px-Square_(geometry).svg.png [ 1.01 KiB | Viewed 160063 times ]
Properties and Tips
• If the diagonals of a rhombus are equal, then that rhombus must be a square. The diagonals of a square are (about 1.414) times the length of a side of the square.
• A square can also be defined as a rectangle with all sides equal, or a rhombus with all angles equal, or a parallelogram with equal diagonals that bisect the angles.
• If a figure is both a rectangle (right angles) and a rhombus (equal edge lengths), then it is a square. (Rectangle (four equal angles) + Rhombus (four equal sides) = Square)
• If a circle is circumscribed around a square, the area of the circle is \(\frac{\pi}{2}\) (about 1.57) times the area of the square.
• If a circle is inscribed in the square, the area of the circle is \(\frac{\pi}{4}\) (about 0.79) times the area of the square.
• A square has a larger area than any other quadrilateral with the same perimeter.
• Like most quadrilaterals, the area is the length of one side times the perpendicular height. So in a square this is simply: \(area=s^2\), where \(s\) is the length of one side.
• The "diagonals" method. If you know the lengths of the diagonals, the area is half the product of the diagonals. Since both diagonals are congruent (same length), this simplifies to: \(area=\frac{d^2}{2}\), where \(d\) is the length of either diagonal
• Each diagonal of a square is the perpendicular bisector of the other. That is, each cuts the other into two equal parts, and they cross and right angles (90°).
• The length of each diagonal is \(s\sqrt{2}\) where \(s\) is the length of any one side.
A square is both a rhombus (equal sides) and a rectangle (equal angles) and therefore has all the properties of both these shapes, namely:
The diagonals of a square bisect each other.
• The diagonals of a square bisect its angles.
• The diagonals of a square are perpendicular.
• Opposite sides of a square are both parallel and equal.
• All four angles of a square are equal. (Each is 360/4 = 90 degrees, so every angle of a square is a right angle.)
• The diagonals of a square are equal.
A square can be thought of as a special case of other quadrilaterals, for example
• a rectangle but with adjacent sides equal
• a parallelogram but with adjacent sides equal and the angles all 90°
• a rhombus but with angles all 90°
Rhombus A quadrilateral with all four sides equal in length. 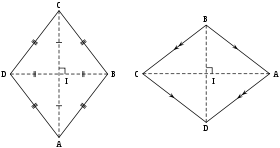
280px-Rhombus.svg.png [ 5.78 KiB | Viewed 165100 times ]
Properties and Tips
• A rhombus is actually just a special type of parallelogram. Recall that in a parallelogram each pair of opposite sides are equal in length. With a rhombus, all four sides are the same length. It therefore has all the properties of a parallelogram.
• The diagonals of a rhombus always bisect each other at 90°.
• There are several ways to find the area of a rhombus. The most common is: \(base*altitude\).
• The "diagonals" method. Another simple formula for the area of a rhombus when you know the lengths of the diagonals. The area is half the product of the diagonals. As a formula: \(\frac{d1*d2}{2}\), where \(d1\) is the length of a diagonal \(d2\) is the length of the other diagonal.
Trapezoid A quadrilateral which has at least one pair of parallel sides. 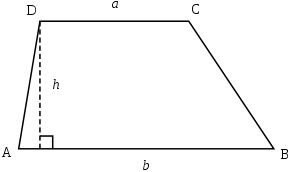
292px-Trapezoid.svg.png [ 2.66 KiB | Viewed 159826 times ]
Properties and Tips
• Base - One of the parallel sides. Every trapezoid has two bases.
• Leg - The non-parallel sides are legs. Every trapezoid has two legs.
• Altitude - The altitude of a trapezoid is the perpendicular distance from one base to the other. (One base may need to be extended).
• If both legs are the same length, this is called an isosceles trapezoid, and both base angles are the same.
• If the legs are parallel, it now has two pairs of parallel sides, and is a parallelogram.
• Median - The median of a trapezoid is a line joining the midpoints of the two legs.
• The median line is always parallel to the bases.
• The length of the median is the average length of the bases, or using the formula: \(\frac{AB+DC}{2}\)
• The median line is halfway between the bases.
• The median divides the trapezoid into two smaller trapezoids each with half the altitude of the original.
• Area - The usual way to calculate the area is the average base length times altitude. The area of a trapezoid is given by the formula \(h*\frac{a+b}{2}\) where
\(a\), \(b\) are the lengths of the two bases \(h\) is the altitude of the trapezoid
• The area of a trapezoid is the \(altitude*median\).
--------------------------------------------------------
Get The Official GMAT Club's App - GMAT TOOLKIT 2.
The only app you need to get 700+ score!
[iOS App] [Android App]
--------------------------------------------------------
created by: Bunuel
edited by: bb, walker
--------------------------------------------------------
This post is a part of [GMAT MATH BOOK]
--------------------------------------------------------
Get The Official GMAT Club's App - GMAT TOOLKIT 2.
The only app you need to get 700+ score!
[iOS App] [Android App]
--------------------------------------------------------
Types of Polygon
Regular A polygon with all sides and interior angles the same. Regular polygons are always convex.
Convex All interior angles less than 180°, and all vertices 'point outwards' away from the interior. The opposite of concave. Regular polygons are always convex.
Definitions, Properties and Tips
• Sum of Interior Angles \(180(n-2)\) where \(n\) is the number of sides
• For a regular polygon, the total described above is spread evenly among all the interior angles, since they all have the same values. So for example the interior angles of a pentagon always add up to 540°, so in a regular pentagon (5 sides), each one is one fifth of that, or 108°. Or, as a formula, each interior angle of a regular polygon is given by: \(\frac{180(n-2)}{n}\), where \(n\) is the number of sides.
• The apothem of a polygon is a line from the center to the midpoint of a side. This is also the inradius - the radius of the incircle.
Attachment:
polyincircle.gif [ 2.68 KiB | Viewed 160880 times ]
Attachment:
polycircumcircle.gif [ 2.91 KiB | Viewed 160774 times ]
GMAT is dealing mainly with the following polygons:
Quadrilateral A polygon with four 'sides' or edges and four vertices or corners.
Attachment:
661px-Quadrilaterals.svg.png [ 24.04 KiB | Viewed 163704 times ]
Square All sides equal, all angles 90°. See Definition of a square.
Rectangle Opposite sides equal, all angles 90°. See Definition of a rectangle.
Parallelogram Opposite sides parallel. See Definition of a parallelogram.
Trapezoid Two sides parallel. See Definition of a trapezoid.
Rhombus Opposite sides parallel and equal. See Definition of a rhombus.
Parallelogram A quadrilateral with two pairs of parallel sides.
Attachment:
255px-Parallelogram.svg.png [ 6.3 KiB | Viewed 169406 times ]
• Opposite sides of a parallelogram are equal in length.
• Opposite angles of a parallelogram are equal in measure.
• Opposite sides of a parallelogram will never intersect.
• The diagonals of a parallelogram bisect each other.
• Consecutive angles are supplementary, add to 180°.
• The area, \(A\), of a parallelogram is \(A = bh\), where \(b\) is the base of the parallelogram and \(h\) is its height.
• The area of a parallelogram is twice the area of a triangle created by one of its diagonals.
A parallelogram is a quadrilateral with opposite sides parallel and congruent. It is the "parent" of some other quadrilaterals, which are obtained by adding restrictions of various kinds:
• A rectangle is a parallelogram but with all angles fixed at 90°
• A rhombus is a parallelogram but with all sides equal in length
• A square is a parallelogram but with all sides equal in length and all angles fixed at 90°
Rectangle A 4-sided polygon where all interior angles are 90°
Attachment:
250px-Rectangle_.png [ 752 Bytes | Viewed 160339 times ]
• Opposite sides are parallel and congruent
• The diagonals bisect each other
• The diagonals are congruent
• A square is a special case of a rectangle where all four sides are the same length.
• It is also a special case of a parallelogram but with extra limitation that the angles are fixed at 90°.
• The two diagonals are congruent (same length).
• Each diagonal bisects the other. In other words, the point where the diagonals intersect (cross), divides each diagonal into two equal parts.
• Each diagonal divides the rectangle into two congruent right triangles. Because the triangles are congruent, they have the same area, and each triangle has half the area of the rectangle.
• \(Diagonal=\sqrt{w^2+h^2}\) where: \(w\) is the width of the rectangle, h is the height of the rectangle.
• The area of a rectangle is given by the formula \(Width*Height\).
A rectangle can be thought about in other ways:
• A square is a special case of a rectangle where all four sides are the same length. Adjust the rectangle above to create a square.
• It is also a special case of a parallelogram but with extra limitation that the angles are fixed at 90°.
Squares A 4-sided regular polygon with all sides equal and all internal angles 90°
Attachment:
220px-Square_(geometry).svg.png [ 1.01 KiB | Viewed 160063 times ]
• If the diagonals of a rhombus are equal, then that rhombus must be a square. The diagonals of a square are (about 1.414) times the length of a side of the square.
• A square can also be defined as a rectangle with all sides equal, or a rhombus with all angles equal, or a parallelogram with equal diagonals that bisect the angles.
• If a figure is both a rectangle (right angles) and a rhombus (equal edge lengths), then it is a square. (Rectangle (four equal angles) + Rhombus (four equal sides) = Square)
• If a circle is circumscribed around a square, the area of the circle is \(\frac{\pi}{2}\) (about 1.57) times the area of the square.
• If a circle is inscribed in the square, the area of the circle is \(\frac{\pi}{4}\) (about 0.79) times the area of the square.
• A square has a larger area than any other quadrilateral with the same perimeter.
• Like most quadrilaterals, the area is the length of one side times the perpendicular height. So in a square this is simply: \(area=s^2\), where \(s\) is the length of one side.
• The "diagonals" method. If you know the lengths of the diagonals, the area is half the product of the diagonals. Since both diagonals are congruent (same length), this simplifies to: \(area=\frac{d^2}{2}\), where \(d\) is the length of either diagonal
• Each diagonal of a square is the perpendicular bisector of the other. That is, each cuts the other into two equal parts, and they cross and right angles (90°).
• The length of each diagonal is \(s\sqrt{2}\) where \(s\) is the length of any one side.
A square is both a rhombus (equal sides) and a rectangle (equal angles) and therefore has all the properties of both these shapes, namely:
The diagonals of a square bisect each other.
• The diagonals of a square bisect its angles.
• The diagonals of a square are perpendicular.
• Opposite sides of a square are both parallel and equal.
• All four angles of a square are equal. (Each is 360/4 = 90 degrees, so every angle of a square is a right angle.)
• The diagonals of a square are equal.
A square can be thought of as a special case of other quadrilaterals, for example
• a rectangle but with adjacent sides equal
• a parallelogram but with adjacent sides equal and the angles all 90°
• a rhombus but with angles all 90°
Rhombus A quadrilateral with all four sides equal in length.
Attachment:
280px-Rhombus.svg.png [ 5.78 KiB | Viewed 165100 times ]
• A rhombus is actually just a special type of parallelogram. Recall that in a parallelogram each pair of opposite sides are equal in length. With a rhombus, all four sides are the same length. It therefore has all the properties of a parallelogram.
• The diagonals of a rhombus always bisect each other at 90°.
• There are several ways to find the area of a rhombus. The most common is: \(base*altitude\).
• The "diagonals" method. Another simple formula for the area of a rhombus when you know the lengths of the diagonals. The area is half the product of the diagonals. As a formula: \(\frac{d1*d2}{2}\), where \(d1\) is the length of a diagonal \(d2\) is the length of the other diagonal.
Trapezoid A quadrilateral which has at least one pair of parallel sides.
Attachment:
292px-Trapezoid.svg.png [ 2.66 KiB | Viewed 159826 times ]
• Base - One of the parallel sides. Every trapezoid has two bases.
• Leg - The non-parallel sides are legs. Every trapezoid has two legs.
• Altitude - The altitude of a trapezoid is the perpendicular distance from one base to the other. (One base may need to be extended).
• If both legs are the same length, this is called an isosceles trapezoid, and both base angles are the same.
• If the legs are parallel, it now has two pairs of parallel sides, and is a parallelogram.
• Median - The median of a trapezoid is a line joining the midpoints of the two legs.
• The median line is always parallel to the bases.
• The length of the median is the average length of the bases, or using the formula: \(\frac{AB+DC}{2}\)
• The median line is halfway between the bases.
• The median divides the trapezoid into two smaller trapezoids each with half the altitude of the original.
• Area - The usual way to calculate the area is the average base length times altitude. The area of a trapezoid is given by the formula \(h*\frac{a+b}{2}\) where
\(a\), \(b\) are the lengths of the two bases \(h\) is the altitude of the trapezoid
• The area of a trapezoid is the \(altitude*median\).
--------------------------------------------------------
Get The Official GMAT Club's App - GMAT TOOLKIT 2.
The only app you need to get 700+ score!
[iOS App] [Android App]
--------------------------------------------------------
Kudos
Bookmarks
Bunuel,
you may add this to your post.
How many diagonals has a polygon with 25 sides?
the formula is:
Number of diagonals in a given polygon is =\(\frac{n*(n-3)}{2}\), where n – is the number of sides.
simple example in a square number of diagonals is =\(\frac{4*(4-3)}{2}=2\)
you may add this to your post.
How many diagonals has a polygon with 25 sides?
the formula is:
Number of diagonals in a given polygon is =\(\frac{n*(n-3)}{2}\), where n – is the number of sides.
simple example in a square number of diagonals is =\(\frac{4*(4-3)}{2}=2\)
Kudos
Bookmarks
logan
Thanks. You are right, changed the variables as you suggested. +1 for good suggestion.
As for the quant book: actually we are working on our very own GMAT MATH BOOK. Of course much work has to be done till completing it: this topic isn't finished yet, we are working on Number Theory, other topics are waiting... But at the end we'll hope to get comprehensive guide to the quant topics of GMAT.










