Forum Home > GMAT > Quantitative > Problem Solving (PS)
Events & Promotions
|
|
GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Dec 1310:00 AM EST
-12:00 PM EST
Have you ever wondered how to score a PERFECT 805 on the GMAT? Meet Julia, a banking professional who used the Target Test Prep course to achieve this incredible feat. Julia's story is nothing short of an inspiration.
Dec 1410:00 AM EST
-12:00 PM EST
Think a 100% GMAT Verbal score is out of your reach? Target Test Prep will make you think again! Our course uses techniques such as topical study and spaced repetition to maximize knowledge retention and make studying simple and fun.
Dec 1411:00 AM IST
-01:00 PM IST
Attend this session to learn how to Deconstruct arguments, Pre-Think Author’s Assumptions, and apply Negation Test.- Dec 15
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. 
Dec 1608:00 AM PST
-11:59 PM PST
GMAT Club 12 Days of Christmas is a 4th Annual GMAT Club Winter Competition based on solving questions. This is the Winter GMAT competition on GMAT Club with an amazing opportunity to win over $40,000 worth of prizes!- Dec 17
09:00 AM PST
-10:00 AM PST
Join Manhattan Prep instructor Whitney Garner for a fun—and thorough—review of logic-based (non-math) problems, with a particular emphasis on Data Sufficiency and Two-Parts. - Dec 18
10:00 AM PST
-11:00 AM PST
Here is the essential guide to securing scholarships as an MBA student! In this video, we explore the various types of scholarships available, including need-based and merit-based options.
So you're like me and hate inequalities. I've come up with a way to determine what an equality looks like on a graph without plugging in points or solving any math.
Most inequalities look like this:
±x±y<±k OR ±x±y>±k where k is a constant
This is important to know, because each sign in the equality will tell you something important about the graph.
+x indicates you keep EVERYTHING normal (I'll explain later)
+y indicates a NEGATIVE slope
< indicates you shade to the left (<---)
+k indicates the x-intercept is positive (to the right of the origin)
-x indicates you FLIP EVERYTHING (slope, direction of shading, x-int)
-y indicates POSITIVE slope
> indicates you shade to the RIGHT (--->)
-k indicates the x-intercept is negative
Example:
3x+4y<3
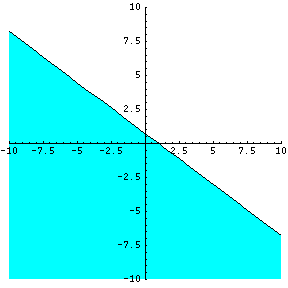
1.gif [ 1.87 KiB | Viewed 26434 times ]
You look at +3x and know you don't have to do anything with that since it's positive.
+4y indicates the slope is NEGATIVE (it's the opposite of +)
< indicates you shade LEFT of the line
and +3 indicates the x-int is to the RIGHT of the origin
-2x+5y<-3
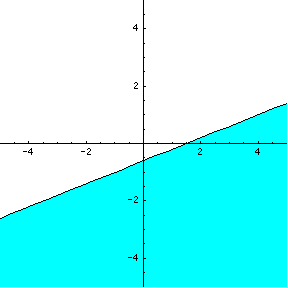
2.gif [ 1.59 KiB | Viewed 26329 times ]
-2x means everything gets REVERSED! Like opposite day...
that means +5y (which originally indicates a negative slope) is now a POSITIVE slope
and < means you shade to the RIGHT (not the left as usual)
and -3 means the x-int is POSITIVE (not negative, since x is negative)
Got it?
It's a little something to memorize, but I believe it would help a lot in combination with Walker's Graphic Approach located here: https://gmatclub.com/forum/7-t68037. I think it would definitely save a lot of time when working on some DS problems, which are KNOWN to have tons of inequalities.
Tell me what you think. This is my first post, so go easy on me
I can do more examples if you need!
If you're looking for a tool to create graphs as an image, you can use this website:
https://www.hostsrv.com/webmab/app1/MSP/ ... s&s3=basic
Just plug in the inequation/equation and generate. Then save your pic!
Most inequalities look like this:
±x±y<±k OR ±x±y>±k where k is a constant
This is important to know, because each sign in the equality will tell you something important about the graph.
+x indicates you keep EVERYTHING normal (I'll explain later)
+y indicates a NEGATIVE slope
< indicates you shade to the left (<---)
+k indicates the x-intercept is positive (to the right of the origin)
-x indicates you FLIP EVERYTHING (slope, direction of shading, x-int)
-y indicates POSITIVE slope
> indicates you shade to the RIGHT (--->)
-k indicates the x-intercept is negative
Example:
3x+4y<3
Attachment:
1.gif [ 1.87 KiB | Viewed 26434 times ]
+4y indicates the slope is NEGATIVE (it's the opposite of +)
< indicates you shade LEFT of the line
and +3 indicates the x-int is to the RIGHT of the origin
-2x+5y<-3
Attachment:
2.gif [ 1.59 KiB | Viewed 26329 times ]
that means +5y (which originally indicates a negative slope) is now a POSITIVE slope
and < means you shade to the RIGHT (not the left as usual)
and -3 means the x-int is POSITIVE (not negative, since x is negative)
Got it?
It's a little something to memorize, but I believe it would help a lot in combination with Walker's Graphic Approach located here: https://gmatclub.com/forum/7-t68037. I think it would definitely save a lot of time when working on some DS problems, which are KNOWN to have tons of inequalities.
Tell me what you think. This is my first post, so go easy on me
I can do more examples if you need!Nach0
Here's a link where you can test out what you've just learned:
https://wims.unice.fr/wims/en_H6~analysi ... eq.en.html
In "Type of Region" select Linear I or Linear II.
It will either provide you with a graph or an inequality. From then you must match it with the corrersponding answer.
You can practice taking what you've learned and applying right away. It will help to quickly determine what kind of grap you are working with.
https://wims.unice.fr/wims/en_H6~analysi ... eq.en.html
In "Type of Region" select Linear I or Linear II.
It will either provide you with a graph or an inequality. From then you must match it with the corrersponding answer.
You can practice taking what you've learned and applying right away. It will help to quickly determine what kind of grap you are working with.
If you're looking for a tool to create graphs as an image, you can use this website:
https://www.hostsrv.com/webmab/app1/MSP/ ... s&s3=basic
Just plug in the inequation/equation and generate. Then save your pic!
10 Nov 2009, 16:15
Kudos
Bookmarks
This is a very good post. Quick solving is the key in GMAT and this certainly goes a long way in helping!
There is one thing I would like to add though.
Suppose we encounter an equation in which we are required to multiply or divide by the variable x or y (as in the question explained by walker in his topic dealing with graphs), then we have to simply break it up into two cases and solve it.
Let me take the following equation as an example (those of you who have gone through walkers post might recognize this equation):
\((x/y) > 2\)
now in order to plot it using the 'quick' approach, we have to break it up in to two cases.
1) When y is positive:
\(x > 2y\) which can be written as \(x - 2y > 0\)
This case gives us the required line. However, it only gives us the region for y>0.
To find the region for y<0, we need case 2.
2) When y is negative:
\((x/-y) > 2\) , now multiply both sides with -1 and simplify.
we get \(x + 2y < 0\)
This case gives us the region for all y<0.
Thus from the above two cases, we infer that:
1) For all positive values of y, the region lies to the right (as given by the equation in case 1).
2) For all negative values of y, the region lies to the left (as given by the equation in case 2).
Note: x = 0 is the line above which all y is positive and below which all y is negative. Thus, it will act as a boundary line. Also, while plotting the line, we should think of an '=' present instead of the inequality in the original equation. The inequality comes into the picture when we want to plot the region.
There is one thing I would like to add though.
Suppose we encounter an equation in which we are required to multiply or divide by the variable x or y (as in the question explained by walker in his topic dealing with graphs), then we have to simply break it up into two cases and solve it.
Let me take the following equation as an example (those of you who have gone through walkers post might recognize this equation):
\((x/y) > 2\)
now in order to plot it using the 'quick' approach, we have to break it up in to two cases.
1) When y is positive:
\(x > 2y\) which can be written as \(x - 2y > 0\)
This case gives us the required line. However, it only gives us the region for y>0.
To find the region for y<0, we need case 2.
2) When y is negative:
\((x/-y) > 2\) , now multiply both sides with -1 and simplify.
we get \(x + 2y < 0\)
This case gives us the region for all y<0.
Thus from the above two cases, we infer that:
1) For all positive values of y, the region lies to the right (as given by the equation in case 1).
2) For all negative values of y, the region lies to the left (as given by the equation in case 2).
Note: x = 0 is the line above which all y is positive and below which all y is negative. Thus, it will act as a boundary line. Also, while plotting the line, we should think of an '=' present instead of the inequality in the original equation. The inequality comes into the picture when we want to plot the region.
Attachments
tarek99.png [ 17.7 KiB | Viewed 16102 times ]
General Discussion
