CAMANISHPARMAR wrote:
Romeo and Juliet play a dice game in which the two participants take turns rolling a single fair six-sided die. The first player to roll a 6 wins. If Romeo rolls first, what is the probability that Juliet will win?
A) \(\frac{1}{4}\)
B) \(\frac{1}{3}\)
C) \(\frac{4}{9}\)
D) \(\frac{5}{11}\)
E) \(\frac{1}{2}\)
(Lets consider the SIMPLE CASE first) the probability of Juliet winning the game considering Romeo looses in first turn and Juliet wins in second turn was \(\frac{5}{6}*\frac{1}{6}\) = \(\frac{5}{36}\)
But what if Juliet does not win in the her first turn but wins in her second turn. Then we have a scenerio where Romeo looses, Juliet also looses, again Romeo looses & finally Juliet wins which translates into \(\frac{5}{6}*\frac{5}{6}*\frac{5}{6}*\frac{1}{6}\)
The total probability that juliet wins in either of her first two chances will be sum of the individual probabilities of she either winning in her first or second chance.
= \(\frac{5}{6}*\frac{1}{6}\)+ \(\frac{5}{6}*\frac{5}{6}*\frac{5}{6}*\frac{1}{6}\)
Similarly:-
The total probability that juliet wins in either of the first THREE chances is
= \(\frac{5}{6}*\frac{1}{6}\) + \(\frac{5}{6}*\frac{5}{6}*\frac{5}{6}*\frac{1}{6}\) + \(\frac{5}{6}*\frac{5}{6}*\frac{5}{6}*\frac{5}{6} *\frac{5}{6}*\frac{1}{6}\)
We can continue like this towards infinity & if we take out \(\frac{5}{6}*\frac{1}{6}\) from this series, we realise that this is a geometric progression with common ratio, r = \(\frac{5}{6}*\frac{5}{6}\)
If we add the probabilities of all individual possible events... we have....
\(\frac{5}{6}*\frac{1}{6}\) + \(\frac{5}{6}*\frac{5}{6}*\frac{5}{6}*\frac{1}{6}\) + \(\frac{5}{6}*\frac{5}{6}*\frac{5}{6}*\frac{5}{6} *\frac{5}{6}*\frac{1}{6}\) + ..... so on
Note the formula for a sum of GP is:-
Attachment:
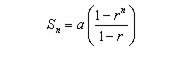 GP sum.jpg [ 2.28 KiB | Viewed 10564 times ]
GP sum.jpg [ 2.28 KiB | Viewed 10564 times ]
Since common ratio of this GP is less than one then \(r^n\) (where n is infinite) means \(r^n\) will become very minute and we can ignore it.
Attachment:
 Expo.jpg [ 19.49 KiB | Viewed 10521 times ]
Expo.jpg [ 19.49 KiB | Viewed 10521 times ]
Therefore substituting the values of a = \(\frac{5}{6}*\frac{1}{6}\) and \(r^n\) = 0 and r = \(\frac{5}{6}*\frac{5}{6}\) we get:-
\(\frac{5}{6}*\frac{1}{6}\)*\(\frac{36}{11}\) = \(\frac{5}{11}\) (Ans)
Hence option D is the correct option.
_________________



 85%
(hard)
85%
(hard)
 50%
(02:24)
wrong
50%
(02:24)
wrong  based on 278
sessions
based on 278
sessions









