The students in a literature class have been assigned to read pages 85

Question

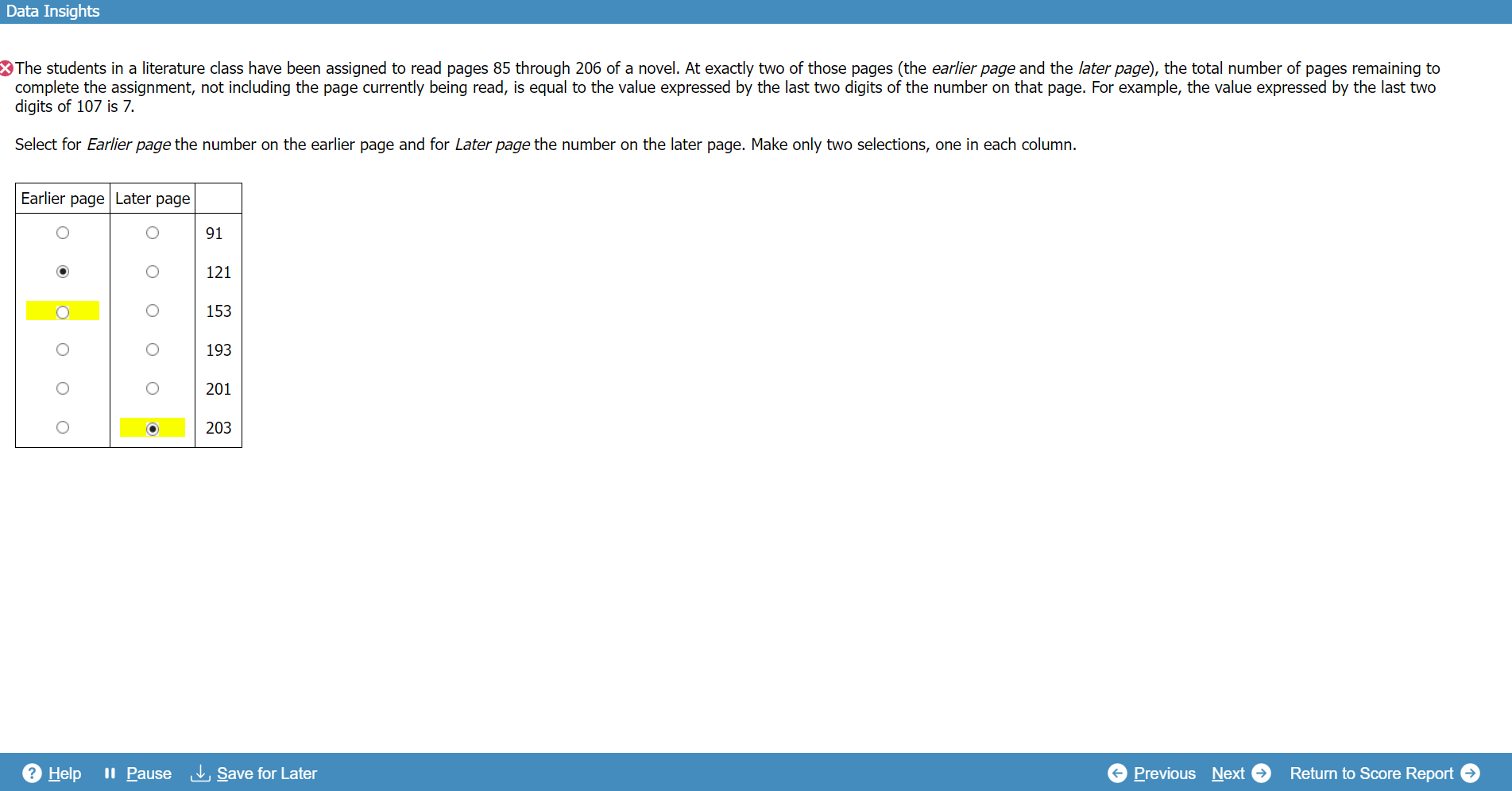
The students in a literature class have been assigned to read pages 85 through 206 of a novel. At exactly two of those pages (the earlier page and the later page), the total number of pages remaining to complete the assignment, not including the page currently being read, is equal to the value expressed by the last two digits of the number on that page. For example, the value expressed by the last two digits of 107 is 7.

Select for Earlier page the number on the earlier page and for Later page the number on the later page. Make only two selections, one in each column.

Show Spoiler

Attachment:

GMAT-Club-Forum-ynup9i8f.png [ 78.39 KiB | Viewed 3280 times ]

Submit Answer

Start the Timer above, select the radio buttons, and click "Submit" to add this question to your Error log.

Show Answer

Official Answer

Earlier page: 153 Later page: 203

GMATCoachBen · Accepted Answer

Once we understand what it's asking, this one can be done quite quickly. Rather than writing anything or doing algebra, I prefer to quickly test the answer choices by adding the final 2 digits, and seeing if we get the total number of pages, 206.

Glancing at the answer choices:

153 + 53 = 206

203 + 3 = 206

So, our answers are  153  and  203 .

Or, to break down the meaning step-by-step, we could translate the wording directly into an equation:

the total number of pages remaining to complete the assignment, not including the page currently being read, is equal to the value expressed by the last two digits of the number on that page.

Logically, how do we represent "the total number of pages remaining"?

Pages Remaining = Total Pages - Current Page

Pages Remaining = last 2 digits of the Current Page  (direct translation of the blue text above)

Rearranging and combining these 2 equations:

Total Pages = Pages Remaining + Current Page = last 2 digits of the Current Page + Current Page

We are told that there are 206 total pages:

206 =  153  + 53

206 =  203  + 3

Aditya8624 · Answer

If we take 153 the earlier page, do we have to consider the page that is being read as it is mentioned not to include that, it a bit confusing there, do we need to subtract that one page?

GMATCoachBen · Answer

No, there is no subtraction of one page, that is overcomplicating things. Just stick to exactly what the passage says:

"At exactly two of those pages (the earlier page and the later page), the total number of pages remaining to complete the assignment,   not including the page currently being read  ,  is equal to the value expressed by the last two digits of the number on that page ."

As a simple example, if we were on page 3 of a 5-page book, there would be 5 - 3 = 2 pages remaining,  not including the page currently being read . Just pages 4 and 5 would be remaining.

Also, as a general thing, we can re-evaluate our approach if we see that none of the answer choices work. If you did decide to subtract one, you would see that none of the answers would work, and that would be a clue that this extra step is not necessary.

chetan2u · Answer

An apt question to use the options. Thu option plus the last two digits should give you 206. 153+53 = 206 = 203+03 But say, you got in a PS and it asked how many such numbers exist It cannot be a 2-digit number, becuas ethen you are looking at double the number and the maximum possible sum would be 99+99 = 198 Any 3-digit number, abc, can be written as 100a+10b+c, so 206 = 100a+10b+c+(10b+c) = 100a+20b+2c ...... 103 = 50a+10b+c..(c would always be 3) If a=1, then 103=50+10b+c ..... 53 = 10b+c....As b and c are digits, b=5 and c=3.....NUmber = 153 If a=2, then 103=100+10b+c ..... 03 = 10b+c....As b and c are digits, b=0 and c=3.....Number = 203 Thus two possibilities as a = 3 will give us sum>300. Earlier = 153 and Later = 203 GMAT-Club-Forum-kw4r7a2z.png

tuyaras · Answer

Once we know what the question wants, it's very easy to find the answer from choice.
During my mock exam, it's so confusing and I end up by guessing the number. So sad.

vivek4141 · Answer

Solving the question was quite straightforward but reading and understanding the question and picturizing it took majority of time.

DUMDUM21 · Answer

This is rather easy question. I tend to complicate all my solutions. Any suggestions for me??

chetan2u · Answer

Just stick to the wording that has been given, and do not get any outside knowledge to it.
Do not assume a question is going to be easy or difficult.

vivek4141 · Answer

Thought process: As last 2 digits would be the pages remaining, it simply means pages remaining <100. Becomes easy by elimination after this as we narrow down the range from pg nos. 85-206 to pg nos. 107-206. Then looking at Options- we get 153 and 203. Hope I have explained. Thanks.

sanebeyondone · Answer

For me this question got me bamboozled in 3 ways:

1. "pages 85" confused me with "85 pages" and number 85 doesn't need to be in the question. The choice starts with 91 which is already higher than 85
2. "not including the page currently being read" is also misguiding . It doesn't need to be in the question and the question will still work perfectly fine.
(It's like saying 1+2 = 3 not inculding 5....)
3. "At exactly two of those pages...." also somehows leads me to think that I need to sum up last 2 digits of those 2 pages.... because I thought the page that is being read is fixed and not moving/varied.
2.+3. well "not including the page currently being read" is what saying that there can be more than 1 page being read. The choices (2PA) also give this clue already, I guess. But the paragraph structure of this question is what killing me.

bumpbot · Answer

Hello from the GMAT Club BumpBot!

Thanks to another GMAT Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).

Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.

The students in a literature class have been assigned to read pages 85

Prep Toolkit

Top 5 GMAT Debrief Videos

615 to 715 in 15 Days (Ria's Strategies)

More than Quant/Verbal Abilities: Speed vs. Accuracy

745 with Only Self-Prep and GMAT Club

From 555 to 765: 210-point Improvement

Perfect 805 Score Debrief by Julia

My Rewards

GMAT Two-part Analysis (TPA) Questions

The students in a literature class have been assigned to read pages 85

Prep Toolkit

615 to 715 in 15 Days (Ria's Strategies)

More than Quant/Verbal Abilities: Speed vs. Accuracy

745 with Only Self-Prep and GMAT Club

From 555 to 765: 210-point Improvement

Perfect 805 Score Debrief by Julia

My Rewards