Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
E
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
 95%
(hard)
95%
(hard)
Question Stats:
33% (01:45) correct 67%
(01:49)
wrong
67%
(01:49)
wrong  based on 1659
sessions
based on 1659
sessions
History
Date
Time
Result
Not Attempted Yet
A certain square is to be drawn on a coordinate plane. One of the vertices must be on the origin, and the square is to have an area of 100. If all coordinates of the vertices must be integers, how many different ways can this square be drawn?
(A) 4
(B) 6
(C) 8
(D) 10
(E) 12
(A) 4
(B) 6
(C) 8
(D) 10
(E) 12
I'll post the official explanation, but it doesn't make sense to me 
Each side of the square must have a length of 10. If each side were to be 6, 7, 8, or most other numbers, there could only be four possible squares drawn, because each side, in order to have integer coordinates, would have to be drawn on the x- or y-axis. What makes a length of 10 different is that it could be the hypotenuse of a Pythagorean triple, meaning the vertices could have integer coordinates without lying on the x- or y-axis.
For example, a square could be drawn with the coordinates (0,0), (6,8), (-2, 14) and (-8, 6). (It is tedious and unnecessary to figure out all four coordinates for each square).
If we label the square abcd, with a at the origin and the letters representing points in a clockwise direction, we can get the number of possible squares by figuring out the number of unique ways ab can be drawn.
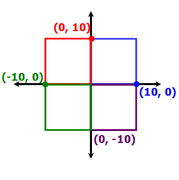
a has coordinates (0,0) and b could have the following coordinates, as shown in the picture:
(-10,0)
(-8,6)
(-6,8)
(0,10)
(6,8)
(8,6)
(10,0)
(8, -6)
(6, -8)
(0, 10)
(-6, -8)
(-8, -6)
There are 12 different ways to draw ab, and so there are 12 ways to draw abcd.
The correct answer is E.
Each side of the square must have a length of 10. If each side were to be 6, 7, 8, or most other numbers, there could only be four possible squares drawn, because each side, in order to have integer coordinates, would have to be drawn on the x- or y-axis. What makes a length of 10 different is that it could be the hypotenuse of a Pythagorean triple, meaning the vertices could have integer coordinates without lying on the x- or y-axis.
For example, a square could be drawn with the coordinates (0,0), (6,8), (-2, 14) and (-8, 6). (It is tedious and unnecessary to figure out all four coordinates for each square).
If we label the square abcd, with a at the origin and the letters representing points in a clockwise direction, we can get the number of possible squares by figuring out the number of unique ways ab can be drawn.
a has coordinates (0,0) and b could have the following coordinates, as shown in the picture:
(-10,0)
(-8,6)
(-6,8)
(0,10)
(6,8)
(8,6)
(10,0)
(8, -6)
(6, -8)
(0, 10)
(-6, -8)
(-8, -6)
There are 12 different ways to draw ab, and so there are 12 ways to draw abcd.
The correct answer is E.
Kudos
Bookmarks
jpr200012
This question becomes much easier if you visualize/draw it.
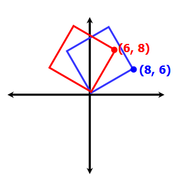
Let the origin be O and one of the vertices be A. Now, we are told that length of OA must be 10 (area to be 100). So if the coordinates of A is (x, y) then we would have \(x^2+y^2=100\) (distance from the origin to the point A(x, y) can be found by the formula \(d^2=x^2+y^2\))
Now, \(x^2+y^2=100\) has several integer solutions for \(x\) and \(y\), so several positions of vertex A, note that when vertex A has integer coordinates other vertices also have integer coordinates. For example imagine the case when square rests on X-axis to the right of Y-axis, then the vertices are: A(10,0), (10,10), (0,10) and (0,0).
Also you can notice that 100=6^2+8^2 and 100=0^2+10^2, so \(x\) can tale 7 values: -10, -8, -6, 0, 6, 8, 10. For \(x=-10\) and \(x=10\), \(y\) can take only 1 value 0, but for other values of \(x\), \(y\) can take two values positive or negative. For example: when \(x=6\) then \(y=8\) or \(y=-8\). This gives us 1+1+5*2=12 coordinates of point A:
\(x=10\) and \(y=0\), imagine this one to be the square which rests on X-axis and to get the other options rotate OA anticlockwise to get all possible cases;
\(x=8\) and \(y=6\);
\(x=6\) and \(y=8\);
\(x=0\) and \(y=10\);
\(x=-6\) and \(y=8\);
\(x=-8\) and \(y=6\);
\(x=-10\) and \(y=0\);
\(x=-8\) and \(y=-6\);
\(x=-6\) and \(y=-8\);
\(x=0\) and \(y=-10\);
\(x=6\) and \(y=-8\);
\(x=8\) and \(y=-6\).
Answer: E.
Kudos
Bookmarks
sandeep800
All 12 squares.
Image posted on our forum by GMATGuruNY:
Attachment:
square.PNG [ 48.28 KiB | Viewed 109221 times ]