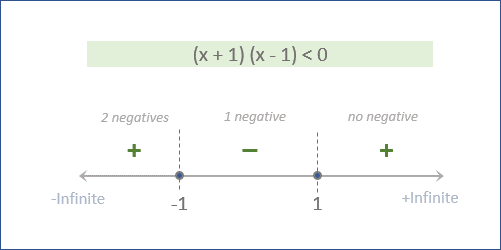Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 19
12:30 PM EST
-01:30 PM EST
Learn how Keshav, a Chartered Accountant, scored an impressive 705 on GMAT in just 30 days with GMATWhiz's expert guidance. In this video, he shares preparation tips and strategies that worked for him, including the mock, time management, and more - Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 20
01:30 PM EST
-02:30 PM IST
Learn how Kamakshi achieved a GMAT 675 with an impressive 96th %ile in Data Insights. Discover the unique methods and exam strategies that helped her excel in DI along with other sections for a balanced and high score. - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 24
07:00 PM PST
-08:00 PM PST
Full-length FE mock with insightful analytics, weakness diagnosis, and video explanations! - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 23 Aug 2018, 04:06.
Last edited by EgmatQuantExpert on 26 Aug 2018, 23:42, edited 2 times in total.
Last edited by EgmatQuantExpert on 26 Aug 2018, 23:42, edited 2 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
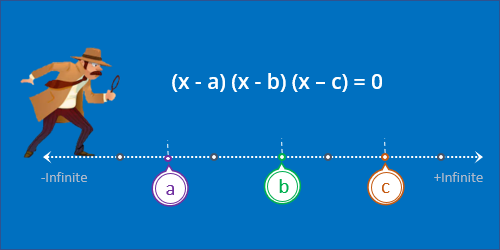
Objective of the Article:
Many of you must be aware of the inequalities and how to solve them algebraically.
In this article, we will discuss:
Agenda of the Article:
So, let us start.
e-GMAT Example 1
Find the range of values of x such that (x-4) (x-8) > 0.
Solution
As we can see that there are two terms (x-4) and (x-8) and we are asked to find the range of x such that their product is greater than zero.
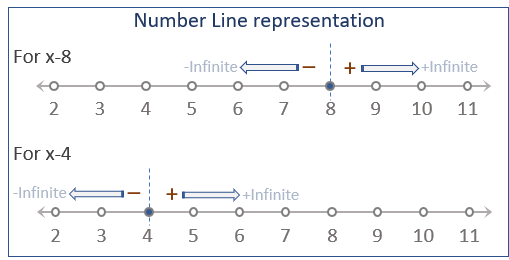
So, let us first draw the number line for (x-4) and (x-8).
Now, to draw the number line for an expression, we first of all highlight the point at which the value of expression is zero.
So, x-4 is zero at x=4 and x-8 is zero at x=8.
Hence, their number line representation will be as follows:
As we can see, for (x-8):
And, similarly for x-4.
However, we need to find the range of x when we multiply both the terms.
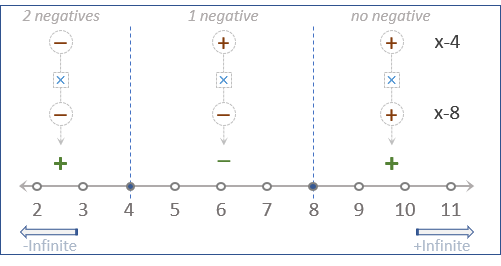
So, let us multiply the positive and negative sign of both the terms.
So, with the help of the above number line, we can say that for all the values of x less than 4 and x greater than 8, (x-4) (x-8)>0.
Before moving on, let us make a few more observations.
So, in every region, starting from the rightmost one, one negative sign is increasing.
Now, don’t you think that finding the sign of any one region will be a long process??
So, let us now make the signs for all the terms in one number line only.
Keeping the above points in our mind, let us solve one polynomial inequality.
e-GMAT Example 2
Find the range of values of x such that (x-1) (x-2) (x-3) > 0.
Solution
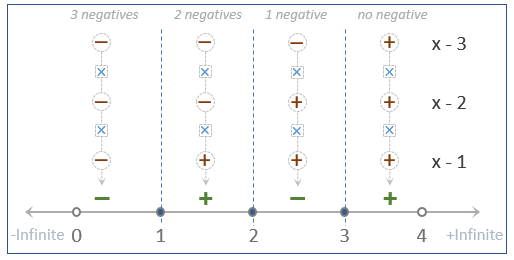
As we can see that the value of polynomial will be zero for x=1, 2, and 3.
So, let us highlight these points on the number light and draw a vertical line.
So, we will make now make the sign for the separate terms i.e. (x-1), (x-2) and (x-3) in one number line only.
Let us first assign the signs in all regions for (x-1).
Let us now assign the signs in all the regions for (x-2).
Similarly, for (x-3):
Now, let us multiply all the signs of the 4 regions.
So, the final sign of the polynomial will be as shown below:
Therefore, (x-1) (x-2) (x-3) will be greater than 0 in 2 regions:
And, even if the question were to find the range of values of x such that (x-1) (x-2) (x-3) < 0, then also, we can find the answer, right??
Now, again, in this example can you notice that:
Similarly, even if the equation were (x-1) (x-2) (x-3) (x-4), we can say that for x>4, all the terms (x-1), (x-2), (x-3), and (x-4) will be positive.
Now, we have found the sign in one region.
So, let us quickly jot down our learning from the above 2 questions.
Key Takeaways
In both the examples, we learnt to solve the inequality of the form \((x {\pm} a)(x {\pm} b)(x {\pm} c)… >=< 0\) by using the number line method.
With this learning, let us solve 3 more questions.
e-GMAT Example 3
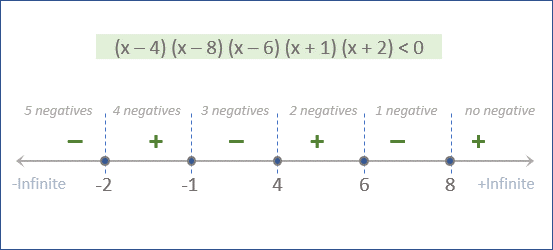
Find the range of values of x such that (x-4)(x-8)(6-x)(x+1)(x+2) > 0.
Solution
Now, is this inequality of the type \((x {\pm} a)(x {\pm} b)(x {\pm} -c)… >=< 0?\)
(x+2), (x+1), (x-4), (x-6), and (x-8) is 0 at x= -2, -1, 4, 6 and 8.
So, let us draw the lines going through these points and assign the positive sign to the rightmost region and then change the signs alternately.
Thus, the number line representation of (x-4) (x-8) (x-6) (x+1) (x+2) is as shown below and it will negative:
We can also represent the range of all the values of x mathematically as (-inf, -2)U(-1,4)U(6, 8).
Let us now move to the next example.
e-GMAT Example 4
Find the range of values of a such that \((a-2)^2 (10-2a) (7+a)^3 > 0.\)
Solution
Now, is \((a-2)^2 (10-2a) (7+a)^3\) written in the form of \((x {\pm} a)(x {\pm} b)(x {\pm} -c)… >=< 0?\)
Now, let us quickly jot down all the learnings from questions 3 and 4.
Key Takeaways
With this learning, let us move forward.
e-GMAT Example 5
Find the range of values of a such that \(\frac{(x-1)}{(x+1)} < 0\).
Solution
Now, we have to find the range of values of x for which the division of x-1 by x+1 is less than 0.
But, do we know how to find the range of division of two expressions?
So, let us write down our learnings from this question.
Key Takeaways
So, now we have come to the end of this article.
Let us once summarize all our learnings from this article.
Key-takeaways from the article
Now, keeping all these learnings in mind, solve the practice questions.
Their link is given in the first comment of this article.
Want to read more articles like this?
Now, if you liked this article, then I am sure that you want to read some more articles like this.
To read all our article go here:Must Read Articles and Practice Questions to score Q51 !!!!
You will also get a lot of practice questions to learn from.
Happy learning.
Solving inequalities- Number Line Method
Objective of the Article:
Many of you must be aware of the inequalities and how to solve them algebraically.
In this article, we will discuss:
- • How we can solve inequalities using the number line method.
• And, we will also learn some key points that will help us to solve any polynomial inequality easily.
Agenda of the Article:
- • We will start this article by taking a small example to help you understand what number line method is.
• Then, we will solve a few more polynomial inequalities and see the application of number line method in those questions.
So, let us start.
e-GMAT Example 1
Find the range of values of x such that (x-4) (x-8) > 0.
Solution
As we can see that there are two terms (x-4) and (x-8) and we are asked to find the range of x such that their product is greater than zero.
So, let us first draw the number line for (x-4) and (x-8).
Now, to draw the number line for an expression, we first of all highlight the point at which the value of expression is zero.
- • And then, we draw a vertical line from those points.
• Finally, we assign the positive/ negative sign to the left and the right region of the vertical line.
So, x-4 is zero at x=4 and x-8 is zero at x=8.
Hence, their number line representation will be as follows:
As we can see, for (x-8):
- • All the values of x lying to the right of 8 will give positive values of x-8
• And, all the values of x lying to the left of 8 will give negative values of x-8.
And, similarly for x-4.
- • All the values of x lying to the right of 4 will give positive values of x-4
• And, all the values of x lying to the left of 4 will give negative values of x-4.
However, we need to find the range of x when we multiply both the terms.
So, let us multiply the positive and negative sign of both the terms.
- • Now, this is the tricky part.
- o If we multiply the signs when x<4 then both x-4 and x-8 is negative
- However, the product of negative *negative = positive.
- • Hence, for x<4, (x-4) (x-8)>0.
- o If we multiply the signs when x>8 then both x-4 and x-8 is positive.
- Hence, for x>8, (x-4) (x-8)>0.
- o However, if we multiply the signs when 4 < x < 8 then:
- x-4 is positive
and x-8 is negative.
- • Hence, for 4 < x < 8, (x-4) (x-8) < 0.
- • So, we can draw the final number line as shown below.
So, with the help of the above number line, we can say that for all the values of x less than 4 and x greater than 8, (x-4) (x-8)>0.
- • Therefore, x <4 and x >8 is our answer.
Before moving on, let us make a few more observations.
- • Observe that in the rightmost region there is no negative sign.
• In the middle region, there is 1 negative sign.
• In the leftmost region, there are 2 negative signs.
So, in every region, starting from the rightmost one, one negative sign is increasing.
- • And, as we know that the multiplication of the even number of negative signs will give a positive sign.
• Thus, if the sign in one region is positive then the sign of its adjacent regions will be negative and vice-versa.
• So, the sign of regions will change alternately.
• Hence, we have to find the sign the one region only.
- o And, we can find the sign in all the other regions.
Now, don’t you think that finding the sign of any one region will be a long process??
- • As we first have to draw the number line for separate terms
• And, then merge both the number line to get the sign in one region
So, let us now make the signs for all the terms in one number line only.
- • And, then we will multiply them to get the final sign in the all the regions.
Keeping the above points in our mind, let us solve one polynomial inequality.
e-GMAT Example 2
Find the range of values of x such that (x-1) (x-2) (x-3) > 0.
Solution
As we can see that the value of polynomial will be zero for x=1, 2, and 3.
So, let us highlight these points on the number light and draw a vertical line.
- • Therefore, we now have 4 regions.
So, we will make now make the sign for the separate terms i.e. (x-1), (x-2) and (x-3) in one number line only.
Let us first assign the signs in all regions for (x-1).
- • We know for x<1, x-1<0
• Hence, in the region where x < 1, the sign of x-1 is negative.
- o And, in all other regions the sign of x-1 will be positive.
Let us now assign the signs in all the regions for (x-2).
- • x-2<0 for all the values of x<2.
- o Hence, the sign of x-2 in the region x<1 and 1<x<2, is negative.
o And, in all other regions, the sign of x-2 will be positive
Similarly, for (x-3):
- • The sign in x>3 is positive.
• And, in all other regions, the sign of x-3 will be negative.
Now, let us multiply all the signs of the 4 regions.
So, the final sign of the polynomial will be as shown below:
Therefore, (x-1) (x-2) (x-3) will be greater than 0 in 2 regions:
- • (1,2) and (3, +inf).
And, even if the question were to find the range of values of x such that (x-1) (x-2) (x-3) < 0, then also, we can find the answer, right??
- • We just have to select the regions in which the final sign is negative.
• That’s all.
Now, again, in this example can you notice that:
- • The negative sign in the rightmost region is 0 and then it is increasing by 1 in every other region.
Similarly, even if the equation were (x-1) (x-2) (x-3) (x-4), we can say that for x>4, all the terms (x-1), (x-2), (x-3), and (x-4) will be positive.
- • So, their multiplication will give us the positive sign only.
• Hence, we can say in every equation of the form \((x {\pm} a)(x {\pm} b)(x {\pm} -c)… >=< 0\), the sign of the rightmost region will always be positive.
Now, we have found the sign in one region.
- • So, we can now easily determine the signs in all the other regions.
• We know that the sign in the consecutive regions will change alternately due to the presence of negative signs in them.
So, let us quickly jot down our learning from the above 2 questions.
Key Takeaways
In both the examples, we learnt to solve the inequality of the form \((x {\pm} a)(x {\pm} b)(x {\pm} c)… >=< 0\) by using the number line method.
- 1. We first have to highlight all the points where the value of the polynomial is 0.
- a. Then, we have to draw a vertical line from all those points.
2. Then, we can assign the sign to every region by first assigning the positive sign to the rightmost region.
- a. And, then changing the signs alternately in consecutive regions from positive to negative and vice-versa.
With this learning, let us solve 3 more questions.
e-GMAT Example 3
Find the range of values of x such that (x-4)(x-8)(6-x)(x+1)(x+2) > 0.
Solution
Now, is this inequality of the type \((x {\pm} a)(x {\pm} b)(x {\pm} -c)… >=< 0?\)
- • No, right?
• If (6-x) would be written as (x-6) then our inequality would be of the above type.
- • So, how should we solve this inequality?
- o Let us write (6-x) as -(x-6) and get the expression as -(x-4)(x-8)(x-6)(x+1)(x+2)>0
o Now, let’s multiply by a negative sign on both the sides of the inequality.
o And, per our conceptual understanding, we know that multiplying by the negative sign changes the sign of the inequality.
o So, let’s do it.
- • Multiplying by the negative sign will give the inequality as (x-4) (x-8) (x-6) (x+1) (x+2) < 0.
• Now, we know how to solve this inequality.
(x+2), (x+1), (x-4), (x-6), and (x-8) is 0 at x= -2, -1, 4, 6 and 8.
So, let us draw the lines going through these points and assign the positive sign to the rightmost region and then change the signs alternately.
Thus, the number line representation of (x-4) (x-8) (x-6) (x+1) (x+2) is as shown below and it will negative:
- • For all the values of x less than -2
• And, between -1 and 4
• And, between 6 and 8.
We can also represent the range of all the values of x mathematically as (-inf, -2)U(-1,4)U(6, 8).
Let us now move to the next example.
e-GMAT Example 4
Find the range of values of a such that \((a-2)^2 (10-2a) (7+a)^3 > 0.\)
Solution
Now, is \((a-2)^2 (10-2a) (7+a)^3\) written in the form of \((x {\pm} a)(x {\pm} b)(x {\pm} -c)… >=< 0?\)
- • No, right?
- o We have (10-2a) and (7+a) in the expression.
o However, (7+a) is same as (a+7).
- • So, to get the above form, we can multiply by a negative sign and write the above inequality as:
- o \((a-2)^2 (2a-10) (a+7)^3 < 0\)
o Or, \(2(a-2)^2 (a-5) (a+7)^3 < 0\)
o Now, can 2 change the sign of the inequality?
- No, right?
As we already discussed that change in the number of negative sign only changes the sign of the inequality.
And, 2 is a positive number.
Therefore, we can discard 2.
- • So, let us find the range of a for \((a-2)^2 (a-5) (a+7)^3 < 0\)
- o Now, again, can \((a-2)^2\)change the sign of the inequality?
- No, right.
As \((a-2)^2\) can either be 0 or greater than 0.
So, we can ignore \((a-2)^2\).
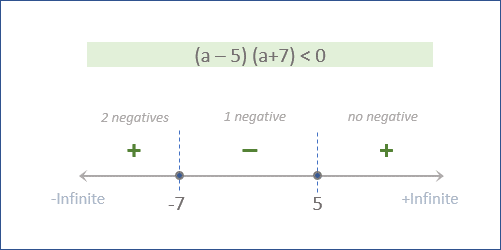
- • Hence, the range of (a-5) (a+7) < 0 will be same as the range of \((a-2)^2 (a-5) (a+7)^3 < 0\).
- • So, we can find the find the sign of (a-5) (a+7) by the number line method as shown.
- o Hence, (a-5)(a+7) is negative for (-7, 5).
o Therefore, the range of \((a-2)^2 (10-2a) (7+a)^ 3 < 0\) is (-7, 5), right?
- No, it’s not correct.
And, it is not correct because when we take the range as (-7, 5), then we also include a=2.
- • However, at a=2, \((a-2)^2 (10-2a) (7+a)^ 3 =0\).
• So, the range of a is all the values of a belonging to (-7, 5) except 2.
- o Which can be mathematically written as (-7, 5) – {2}.
o Here, minus 2 i.e. – {2}, indicates that we are not including a=2 in the range of a.
- • So, we have found our answer.
• However, if the question were to find the range of \((a-2)^2 (10-2a) (7+a)^3 ≤ 0\) then we can include all the points where the value of the expression is 0.
- o So, the range will be= as [-7, 5].
o Here close bracket “[ “ near to -7 and 5 indicate that we are considering -7and 5 in our range.
- However, open bracket “(“ indicates that we are not considering it -7 and 5.
Now, let us quickly jot down all the learnings from questions 3 and 4.
Key Takeaways
- 1. We first learnt that it is very important that polynomial inequality is given as \((x {\pm} a)(x {\pm} b)(x {\pm} -c)… >=< 0\).
- a. And, if not, then we try to convert the given inequality into the above form.
- a. So, we can discard the positive terms from the original inequality.
b. However, make sure that you give proper attention to the constraint and the sign of the inequality given in the question.
With this learning, let us move forward.
e-GMAT Example 5
Find the range of values of a such that \(\frac{(x-1)}{(x+1)} < 0\).
Solution
Now, we have to find the range of values of x for which the division of x-1 by x+1 is less than 0.
But, do we know how to find the range of division of two expressions?
- • No, right.
• So, should we cross-multiply (x+1) with 0?
- o The cross multiplication with x+1 will simplify the inequality and we get x-1<0, right???
- No, it is not correct.
- o Per our conceptual understanding, when we multiply by a positive number then the sign of the inequality does not change.
- However, if we multiply by a negative number then the sign of the inequality changes.
So, do we know that x+1 is certainly positive?
No, right?
- • x can be -10 or -100 or 100.
• So, we cannot cross multiply by (x+1).
• Now, what should we do??
- o Well, we can multiply both the sides of the inequality by \((x+1)^2\), since \((x+1)^2\) is always positive.
- Multiplying will give us the inequality as:
\(\frac{((x+1)^2*(x-1))}{(x+1)}< 0*(x+1)^2 or\ (x+1)(x-1)<0.\)
- • Now, we know how to solve (x+1)(x-1)<0.
- o So, by using the number system method, we can find the sign of (x+1)(x-1) in different regions as shown.
o Hence, the range of x is (-1, 1).
So, let us write down our learnings from this question.
Key Takeaways
- • In this question, we learned that we cannot cross multiply by an expression until we are certain that it is always positive.
• However, we can multiply by the square or even power of the expression as it is always positive.
So, now we have come to the end of this article.
Let us once summarize all our learnings from this article.
Key-takeaways from the article
- • We first learnt how to draw the number line representing signs for a linear expression like x-4 and x-8.
- • Then we learnt how to represent signs on the number line for quadratic and polynomial equations.
- • We also learnt that if the inequality is of the form \((x {\pm} a)(x {\pm} b)(x {\pm} -c)… >=< 0\):
- o Then, while drawing the number line, the sign in right most region is always positive.
o And it changes alternately in consecutive regions.
- • We also learnt that while solving a polynomial inequality, we can discard the term that is always positive.
- • We also saw an example to understand that we can only cross multiply by terms that are always positive.
- o If the term/ expression is not always positive then we cannot cross multiply.
o However, we may cross-multiply by its square or even powers
Now, keeping all these learnings in mind, solve the practice questions.
Their link is given in the first comment of this article.
Want to read more articles like this?
Now, if you liked this article, then I am sure that you want to read some more articles like this.
To read all our article go here:Must Read Articles and Practice Questions to score Q51 !!!!
You will also get a lot of practice questions to learn from.
Happy learning.
Attachments
![]() Solving inequalities - Number Line Method.pdf [821.4 KiB]
Solving inequalities - Number Line Method.pdf [821.4 KiB]
Downloaded 393 times
Kudos
Bookmarks
Hey Everyone,
Here is a list of questions specifically designed to help you apply the learnings from this article.
Practice Questions
Question 1
Question 2
Question 3
Question 4
Detailed solutions will be posted soon.
Happy Learning!
Kudos
Bookmarks
Dear Team,
Kindly posted the PDF to the end of your very useful article!
Kindly posted the PDF to the end of your very useful article!