Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 19
12:30 PM EST
-01:30 PM EST
Learn how Keshav, a Chartered Accountant, scored an impressive 705 on GMAT in just 30 days with GMATWhiz's expert guidance. In this video, he shares preparation tips and strategies that worked for him, including the mock, time management, and more - Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 20
01:30 PM EST
-02:30 PM IST
Learn how Kamakshi achieved a GMAT 675 with an impressive 96th %ile in Data Insights. Discover the unique methods and exam strategies that helped her excel in DI along with other sections for a balanced and high score. - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 24
07:00 PM PST
-08:00 PM PST
Full-length FE mock with insightful analytics, weakness diagnosis, and video explanations! - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 15 Mar 2019, 13:32.
Last edited by EgmatQuantExpert on 24 Mar 2019, 23:19, edited 8 times in total.
Last edited by EgmatQuantExpert on 24 Mar 2019, 23:19, edited 8 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
Why should you read this article?
This article is written for students who do reasonably well on Problem Solving questions yet continue to struggle with Data Sufficiency (DS) questions in Number Properties. Conversely, read this article, if you make mistake on DS questions despite knowing the concepts being tested.
After reading this article you will recognize three common reasons why you make a mistake and the steps you can take to read or eliminate the same.
Agenda of the Article
A major part of solving a DS question correctly involves inferring the information from the question stem…
To help you, we will discuss three major mistakes that students make while applying inferences in a DS question.
These 3 mistakes are:
We will take one question each to discuss the above 3 types of mistakes.
Let us discuss the first mistake.
Mistake 1: Drawing Incorrect Inference from the Question Stem
Many times, a student knows exactly how to solve a question correctly – he knows all the concepts, he even knows how to go about solving the question, yes makes a mistake by drawing incorrect inference(s) from the question stem. The most common reason for the same - rushing through while reading the question stem.
In mistake 1, we will look at one e-GMAT Practice question where students have made this type of mistake.
Let us look at the question first.
e-GMAT Question 1
x, y, and z are positive integers, where x is an odd number and z = \(x^2\) + \(y^2\) + 4. Is \(y^2\) divisible by 4?
(For e-GMAT students: This question is present in the Even-Odd practice quiz of Number properties module)

Accuracy of the question: 55.10%
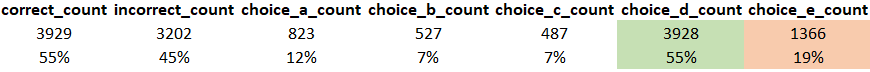
Total relevant forum post queries posted for this question: 14
So, let us understand this question first!
Given:
Inference from the given information:
To Find:
We need to find whether \(y^2\) is divisible by 4 or not.
Inference from what we need to find:
Now, let us first look at one incorrect inference.
Student’s Mistake – Incorrect Inference
Notice the highlighted part of this query.

Now, is there anything wrong in this inference drawn by the student?
Correct Inference
Hence, the correct inference is that if y is divisible by 2 then \(y^2\) will be divisible by 4.
So, if you focus on processing information in the correct manner then you can get the question correct.
How to Avoid Drawing Incorrect Inferences
Mistake 2: Drawing Incomplete Inference from the Question Stem
This is the second type of mistake where students infer incomplete information from the question stem.
To understand the same, let us look at another e-GMAT question.
e-GMAT Question 2
The number x is a positive odd integer. If the unit digit of \(x^3\) is subtracted from the unit digit of \(x^2\), it results in 0. What is the unit digit of the number x + 7?
(For e-GMAT students: This question is present in units digit practice quiz of Number properties module)

Accuracy of the question: 44.47%

Total relevant forum post queries posted for this question: 14
Let us understand why this happened.
Given:
Inference from the given information:
Let us look at one incomplete inference first.
Student’s Mistake: Incomplete Inference

This student thinks that 105 is ending with 5 and its multiplication with another number is also ending with 5.
Note, the student here did spend the time to draw this inference. He also applied the right concepts. Yet, despite this, the inference he drew was incomplete.
Therefore, why don’t you spend some time and try to draw the correct inference.
Correct Inference
Since the subtraction of units digits of \(x^3\) and \(x^2\) are resulting in 0, we can say that their units digits are identical (or equal).
For example:
So, the student made two mistakes.
And, do you know that test makers also form such questions by keeping in minds these traps?
Let us read statement 1 again.
Statement 1: The unit digit of the product of 105 and x is 5.
For units digit of x =1 or 5, the units digit of (105 × x) is 5. For example:
If the student draws an incomplete inference and considers only 5 or only 1, then he will think that statement 1 is sufficient to answer and that is how he will fall into the trap.
How to avoid drawing incomplete inferences
So, we have learned to avoid the 2 most common mistakes in DS questions.
We will discuss “Mistake 3: Faltering while applying the inferences” in the next article.
Takeaways From This Article
Want to read more articles like this?
If you liked this article, then I am sure that you want to read some more articles like this.
To read all our article go here:Must Read Articles and Practice Questions to score Q51
You will also get 50+ practice questions, across various topics, to learn from.
Happy learning.
GMAT Quant DS - 3 Mistakes Students Make in Number Properties Questions - Part I
Why should you read this article?
This article is written for students who do reasonably well on Problem Solving questions yet continue to struggle with Data Sufficiency (DS) questions in Number Properties. Conversely, read this article, if you make mistake on DS questions despite knowing the concepts being tested.
After reading this article you will recognize three common reasons why you make a mistake and the steps you can take to read or eliminate the same.
Agenda of the Article
A major part of solving a DS question correctly involves inferring the information from the question stem…
- • And, this is an area where students typically falter.
To help you, we will discuss three major mistakes that students make while applying inferences in a DS question.
These 3 mistakes are:
- 1. Drawing incorrect inference from the question stem.
2. Drawing incomplete inference from the question stem.
3. Faltering while applying the inferences.
We will take one question each to discuss the above 3 types of mistakes.
- • Note: Since these questions are e-GMAT practice quiz questions, we will also provide the accuracy and total number of forum queries for each question.
Let us discuss the first mistake.
Mistake 1: Drawing Incorrect Inference from the Question Stem
Many times, a student knows exactly how to solve a question correctly – he knows all the concepts, he even knows how to go about solving the question, yes makes a mistake by drawing incorrect inference(s) from the question stem. The most common reason for the same - rushing through while reading the question stem.
In mistake 1, we will look at one e-GMAT Practice question where students have made this type of mistake.
Let us look at the question first.
e-GMAT Question 1
x, y, and z are positive integers, where x is an odd number and z = \(x^2\) + \(y^2\) + 4. Is \(y^2\) divisible by 4?
- 1. z = 8k - 3
2. (z – x + 1) = 2q + 1
(For e-GMAT students: This question is present in the Even-Odd practice quiz of Number properties module)

Accuracy of the question: 55.10%
- Here is the number of responses against each option and the corresponding percentage:
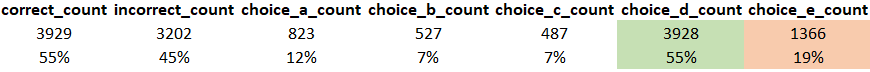
Total relevant forum post queries posted for this question: 14
- • We know that 45% of the students got this question wrong and out of this 45%, every 2 out of the 5 students knew all the concepts and still made the mistake.
So, let us understand this question first!
Given:
- • x, y, and z are positive integer and x is an odd number.
• z = \(x^2\) +\(y^2\) + 4
Inference from the given information:
- • z = Odd + \(y^2\) + Even
• z = Odd + \(y^2\) (As Odd + Even = Odd)
To Find:
We need to find whether \(y^2\) is divisible by 4 or not.
Inference from what we need to find:
Now, let us first look at one incorrect inference.
Student’s Mistake – Incorrect Inference
Notice the highlighted part of this query.

Now, is there anything wrong in this inference drawn by the student?
- • It is actually partially incorrect.
- o The reason is that student is considering only those values of y that are divisible by 4.
o What if y is divisible by 2 only and not divisible by 4?
- For example, what if y = 2 or 6 or 10?
- • Is \(y^2\) = 4 or 36 or 100 not divisible by 4?
• It is.
Correct Inference
Hence, the correct inference is that if y is divisible by 2 then \(y^2\) will be divisible by 4.
- • Or, essentially if y is even then \(y^2\) is divisible by 4.
So, if you focus on processing information in the correct manner then you can get the question correct.
- • The best thing is you don’t need to learn any new concepts, it is only about developing good habits i.e. following step by step and methodical process.
How to Avoid Drawing Incorrect Inferences
- 1. The first reason why students make this mistake is because drawing inferences from question stem is not a part of their process to solve a DS question.
- a. Basically, they start to draw inferences from the statements and that is how they make this mistake.
b. So, make sure to include this step in you process.
2. Secondly, drawing inferences from the question stem may be part of a student’s process of solving a question, yet the student tends to rush while doing the same. Therefore:
- a. The student draws incomplete inferences.
b. Or the student is unable to draw any inference at all.
3. Now there are scenarios in which the student knows the concepts and also spends enough time to draw inferences, and yet is unable to draw the correct inference because the student does not have the depth/capability to draw inferences.
- a. If such is the case, then such questions present excellent learning opportunities. Bookmark this question and revise it at least twice. Doing so will improve your ability to infer and you will make fewer similar mistakes.
Mistake 2: Drawing Incomplete Inference from the Question Stem
This is the second type of mistake where students infer incomplete information from the question stem.
To understand the same, let us look at another e-GMAT question.
e-GMAT Question 2
The number x is a positive odd integer. If the unit digit of \(x^3\) is subtracted from the unit digit of \(x^2\), it results in 0. What is the unit digit of the number x + 7?
- 1. The unit digit of the product of 105 and x is 5.
2. When x is divided by 5, it leaves no remainder.
(For e-GMAT students: This question is present in units digit practice quiz of Number properties module)

Accuracy of the question: 44.47%
- Here is the number of responses against each option and the corresponding percentage:

Total relevant forum post queries posted for this question: 14
- • Out of the 55% who got this question wrong, every 1 out of 3 students knew the concepts and still got the question wrong.
Let us understand why this happened.
Given:
- • x is a positive odd integer.
• When the unit digit of \(x^3\) is subtracted from the unit digit of \(x^2\), it results in 0.
Inference from the given information:
Let us look at one incomplete inference first.
Student’s Mistake: Incomplete Inference

This student thinks that 105 is ending with 5 and its multiplication with another number is also ending with 5.
- • So, he does some calculation in the back of his mind that:
- o 5*5 ends with 5
o 25* 5 also ends with 5
o 125* 5 also ends with 5.
Note, the student here did spend the time to draw this inference. He also applied the right concepts. Yet, despite this, the inference he drew was incomplete.
Therefore, why don’t you spend some time and try to draw the correct inference.
Correct Inference
Since the subtraction of units digits of \(x^3\) and \(x^2\) are resulting in 0, we can say that their units digits are identical (or equal).
- • Units digit of \(x^3\) = Units digit of \(x^2\)
- • Therefore, the possible units digit of odd integers with cyclicity 1 can be either 1 or 5 and not just 5.
For example:
- • For x = 11, last digit of (105 × 11) = last digit of (5 × 1) = 5.
• For x = 31, last digit of (105 × 31) = last digit of (5 × 1) = 5.
• For x = 35, last digit of (105 × 35) = last digit of (5 × 5) = 5.
• For x = 65, last digit of (105 × 65) = last digit of (5 × 5) = 5.
So, the student made two mistakes.
- 1. He forgot to consider that the units digit of x can also be 1 – which is an incomplete inference.
2. He also relied on number substitution which gives wrong answers in many questions.
- a. The reason is simple – you take only one value and do not think for other possible values.
b. As we saw in this question, last digit 5 works but it is not the only value of the last digit of x that works.
And, do you know that test makers also form such questions by keeping in minds these traps?
- • Want to see how…?
Let us read statement 1 again.
Statement 1: The unit digit of the product of 105 and x is 5.
- • Units digit of (105 × x) = 5
For units digit of x =1 or 5, the units digit of (105 × x) is 5. For example:
- 1. Units digit of (105 × 11) = Units digit of (5 × 1) = 5.
2. Units digit of (105 × 25) = Units digit of (5 × 5) = 5.
If the student draws an incomplete inference and considers only 5 or only 1, then he will think that statement 1 is sufficient to answer and that is how he will fall into the trap.
- • And, the only way to ensure that one does not fall into these kinds of traps is to completely and correctly infer all the information present in the question.
How to avoid drawing incomplete inferences
- • You can avoid making incomplete inferences by following a proper step by step and methodical approach in every DS question.
• As in this question, we first found that cyclicity of units digit of x is 1 and then we found two possible values of x rather than directly coming to a value without proper analysis.
• This ensures that we are not missing out any inference that might be useful to solve a question correctly.
So, we have learned to avoid the 2 most common mistakes in DS questions.
We will discuss “Mistake 3: Faltering while applying the inferences” in the next article.
Takeaways From This Article
- 1. We discussed how important it is to draw inferences from question stem.
- a. Please understand that the question stem provides important information that needs to be processed and inferred first.
b. If this step is still not in your process, do add this and your accuracy will improve.
2. Don’t rush through reading the question stem because you might draw incomplete and/or incorrect inferences.
- a. Make a conscious effort to not rush through things. To start off, you can even assign yourself 45 sec – 1 min to process information and with practice, this process will happen automatically every time you will solve a question. Similarly, the time required to infer information will reduce with practice as well.
3. There are some questions in which you spend the time to draw inference from the question stem and yet are make a mistake. Bookmark these questions; treat them as a learning opportunity.
- a. Make notes and such questions a couple of times and your propensity to make such mistakes will reduce.
Want to read more articles like this?
If you liked this article, then I am sure that you want to read some more articles like this.
To read all our article go here:Must Read Articles and Practice Questions to score Q51
You will also get 50+ practice questions, across various topics, to learn from.
Happy learning.
Attachments
![]() 3Mistakes_Number Properties – Part I.pdf [476.24 KiB]
3Mistakes_Number Properties – Part I.pdf [476.24 KiB]
Downloaded 189 times
Kudos
Bookmarks
Kindly add the pdf.
thanks
thanks
Kudos
Bookmarks
Hey Everyone,
We have added the pdf of the article.
Regards,
We have added the pdf of the article.
Regards,













