Forum Home > GMAT > Quantitative > Problem Solving (PS)
Events & Promotions
|
|
GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Jan 1507:30 AM PST
-08:30 AM PST
Studying for the GMAT can feel like a long journey, but having the right plan can keep you on track. In this live session, Julia, who scored a perfect 805, will share her step-by-step study plan for 2025. Join for help with key strategies and tips...
Jan 1610:00 AM EST
-12:00 PM EST
The Target Test Prep team is proud to introduce GMAT OnDemand, a video course created by Scott Woodbury-Stewart, founder and CEO, designed to provide you with everything you need to master the GMAT and achieve your score goals.- Jan 16
10:00 AM PST
-11:00 AM PST
Meet Kseniia, a former Public Relations Head at Google in Russia, whose inspiring journey defied the odds and landed her admissions to Wharton, Chicago Booth, and Yale SOM. - Jan 17
10:00 AM PST
-11:00 AM PST
Keshav who scored 99 percentile with near-perfect quant score shares his strategies and techniques to identify and overcome the weaknesses in his GMAT preparation. Learn the preparation tips and study strategies that worked for him. - Jan 18
10:00 AM PST
-11:00 AM PST
In this video, we talked to Rishi, an ambitious Indian student who successfully secured admission into HEC Paris and ESSEC Business School, two of the top Masters in Management (MiM) programs in Europe. 
Jan 1811:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment- Jan 19
11:00 AM IST
-01:00 PM IST
Attend this session to evaluate your current skill level, learn process skills, and solve through tough Arithmetic questions
05 Jun 2020, 08:34
Kudos
Bookmarks
OG Quantitative Review 2020
QUESTION COLLECTION with VIDEO SOLUTION
by
Bhoopendra Singh (Founder: GMATinsight)
Solve them as Quizzes for FREE (Open Access so no Login) CLICK HERE
Q-1: Working at a constant rate, a copy machine makes 20 copies of a one-page document per minute. If the machine works at this constant rate, how many hours does it take to make 4,800 copies of a one-page document?
A. 4
B. 5
C. 6
D. 7
E. 8
A. 4
B. 5
C. 6
D. 7
E. 8
Q-2: If x + y = 2 and x^2 + y^2 = 2, what is the value of xy ?
A. –2
B. –1
C. 0
D. 1
E. 2
PS11042
A. –2
B. –1
C. 0
D. 1
E. 2
PS11042
Q-3: The sum S of the first n consecutive positive even integers is given by S = n(n + 1). For what value of n is this sum equal to 110 ?
A. 10
B. 11
C. 12
D. 13
E. 14
(PS02978)
A. 10
B. 11
C. 12
D. 13
E. 14
(PS02978)
Q-4:
A certain harbor has docking stations along its west and south docks, as shown in the figure; any two adjacent docking stations are separated by a uniform distance d. A certain boat left the west dock from docking station #2 and moved in a straight line diagonally until it reached the south dock. If the boat was at one time directly east of docking station #4 and directly north of docking station #7, at which docking station on the south dock did the boat arrive?
A. #7
B. #8
C. #9
D. #10
E. #11
(PS08375)
A certain harbor has docking stations along its west and south docks, as shown in the figure; any two adjacent docking stations are separated by a uniform distance d. A certain boat left the west dock from docking station #2 and moved in a straight line diagonally until it reached the south dock. If the boat was at one time directly east of docking station #4 and directly north of docking station #7, at which docking station on the south dock did the boat arrive?
A. #7
B. #8
C. #9
D. #10
E. #11
(PS08375)
Q-5: 6(87.30+0.65)−5(87.30)=
A. 3.90
B. 39.00
C. 90.90
D. 91.20
E. 91.85
(PS03887)
A. 3.90
B. 39.00
C. 90.90
D. 91.20
E. 91.85
(PS03887)
Q-6: Points A, B, C, and D, in that order, lie on a line. If AB = 3 cm, AC = 4 cm, and BD = 6 cm, what is CD, in centimeters?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
PS13800
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
PS13800
Q-7: What is the value of \(x^2yz − xyz^2\), if x = − 2, y = 1, and z = 3?
(A) 20
(B) 24
(C) 30
(D) 32
(E) 48
PS05292
(A) 20
(B) 24
(C) 30
(D) 32
(E) 48
PS05292
Q-8: A souvenir vendor purchased 1,000 shirts for a special event at a price of $5 each. The vendor sold 600 of the shirts on the day of the event for $12 each and 300 of the shirts in the week following the event for $4 each. The vendor was unable to sell the remaining shirts. What was the vendor's gross profit on the sale of these shirts?
A. $1,000
B. $2,200
C. $2,700
D. $3,000
E. $3,400
(PS11468)
A. $1,000
B. $2,200
C. $2,700
D. $3,000
E. $3,400
(PS11468)
Q-9: If x > y and y > z, which of the following represents the greatest number?
(A) x − z
(B) x − y
(C) y − x
(D) z − y
(E) z − x
PS06937
(A) x − z
(B) x − y
(C) y − x
(D) z − y
(E) z − x
PS06937
Q-10: To order certain plants from a catalog, it costs $3.00 per plant, plus a 5 percent sales tax, plus $6.95 for shipping and handling regardless of the number of plants ordered. If Company C ordered these plants from the catalog at the total cost of $69.95, how many plants did Company C order?
A. 22
B. 21
C. 20
D. 19
E. 18
PS12926
A. 22
B. 21
C. 20
D. 19
E. 18
PS12926
Q-11: A rug manufacturer produces rugs at a cost of $75 per rug. What is the manufacturer's gross profit from the sale of 150 rugs if 2/3 of the rugs are sold for $150 per rug and the rest are sold for $200 per rug?
A. $10,350
B. $11,250
C. $13,750
D. $16,250
E. $17,800
(PS00812)
A. $10,350
B. $11,250
C. $13,750
D. $16,250
E. $17,800
(PS00812)
Q-12: The value of Maureen's investment portfolio has decreased by 5.8 percent since her initial investment in the portfolio. If her initial investment was $16,800, what is the current value of the portfolio?
A. $7,056.00
B. $14,280.00
C. $15,825.60
D. $16,702.56
E. $17,774.40
(PS07793)
A. $7,056.00
B. $14,280.00
C. $15,825.60
D. $16,702.56
E. $17,774.40
(PS07793)
Q-13: Company C produces toy trucks at a cost of $5.00 each for the first 100 trucks and $3.50 for each additional truck. If 500 toy trucks were produced by Company C and sold for $10.00 each, what was Company C’s gross profit?
(A) $2,250
(B) $2,500
(C) $3,100
(D) $3,250
(E) $3,500
PS03036
(A) $2,250
(B) $2,500
(C) $3,100
(D) $3,250
(E) $3,500
PS03036
Q-14: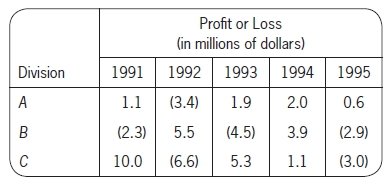 
The annual profit or loss for the three divisions of Company T for the years 1991 through 1995 are summarized in the table shown, where losses are enclosed in parentheses. For which division and which three consecutive years shown was the division's profit or loss for the three-year period closest to $0 ?
A. Division A for 1991–1993
B. Division A for 1992–1994
C. Division B for 1991–1993
D. Division B for 1993–1995
E. Division C for 1992–1994
(PS02019)
The annual profit or loss for the three divisions of Company T for the years 1991 through 1995 are summarized in the table shown, where losses are enclosed in parentheses. For which division and which three consecutive years shown was the division's profit or loss for the three-year period closest to $0 ?
A. Division A for 1991–1993
B. Division A for 1992–1994
C. Division B for 1991–1993
D. Division B for 1993–1995
E. Division C for 1992–1994
(PS02019)
Q-15: Of the following, which is least?
A. \(\frac{0.03}{0.00071}\)
B. \(\frac{0.03}{0.0071}\)
C. \(\frac{0.03}{0.071}\)
D. \(\frac{0.03}{0.71}\)
E. \(\frac{0.03}{7.1}\)
A. \(\frac{0.03}{0.00071}\)
B. \(\frac{0.03}{0.0071}\)
C. \(\frac{0.03}{0.071}\)
D. \(\frac{0.03}{0.71}\)
E. \(\frac{0.03}{7.1}\)
Q-16: If the average (arithmetic mean) of 5 numbers j, j + 5, 2j – 1, 4j – 2, and 5j – 1 is 8, what is the value of j ?
A. \(\frac{1}{3}\)
B. \(\frac{7}{13}\)
C. 1
D. 3
E. 8
A. \(\frac{1}{3}\)
B. \(\frac{7}{13}\)
C. 1
D. 3
E. 8
Q-17: Guadalupe owns 2 rectangular tracts of land. One is 300 m by 500 m and the other is 250 m by 630 m. The combined area of these 2 tracts is how many square meters?
A. 3,360
B. 307,500
C. 621,500
D. 704,000
E. 2,816,000
PS14037
A. 3,360
B. 307,500
C. 621,500
D. 704,000
E. 2,816,000
PS14037
Q-18: There are five sales agents in a certain real estate office. One month Andy sold twice as many properties as Ellen, Bob sold 3 more than Ellen, Cary sold twice as many as Bob, and Dora sold as many as Bob and Ellen together. Who sold the most properties that month?
a) Andy
b) Bob
c) Cary
d) Dora
e) Ellen
PS03918
a) Andy
b) Bob
c) Cary
d) Dora
e) Ellen
PS03918
Q-19: In a field day at a school, each child who competed in \(n\) events and scored a total of \(p\) points was given an overall score of \(\frac{p}{n} + n\). Andrew competed in 1 event and scored 9 points. Jason competed in 3 events and scored 5, 6, and 7 points, respectively. What was the ratio of Andrew's overall score to Jason's overall score?
A. \(\frac{10}{23}\)
B. \(\frac{7}{10}\)
C. \(\frac{4}{5}\)
D. \(\frac{10}{9}\)
E. \(\frac{12}{7}\)
PS10862
A. \(\frac{10}{23}\)
B. \(\frac{7}{10}\)
C. \(\frac{4}{5}\)
D. \(\frac{10}{9}\)
E. \(\frac{12}{7}\)
PS10862
Q-20: A certain work plan for September requires that a work team, working every day, produce an average of 200 items per day. For the first half of the month, the team produced an average of 150 items per day. How many items per day must the team average during the second half of the month if it is to attain the average daily production rate required by the work plan?
A. 225
B. 250
C. 275
D. 300
E. 350
PS06719
A. 225
B. 250
C. 275
D. 300
E. 350
PS06719
Q-21: A company sells radios for $15.00 each. It costs the company $14.00 per radio to produce 1,000 radios and $13.50 per radio to produce 2,000 radios. How much greater will the company's gross profit be from the production and sale of 2,000 radios than from the production and sale of 1,000 radios?
A. $500
B. $1,000
C. $1,500
D. $2,000
E. $2,500
(PS01949)
A. $500
B. $1,000
C. $1,500
D. $2,000
E. $2,500
(PS01949)
Q-22: Which of the following represent positive numbers?
I. −3 − (−5)
II. (− 3)(−5)
III. −5 − (−3)
A. I only
B. II only
C. III only
D. I and II
E. II and III
PS06555
I. −3 − (−5)
II. (− 3)(−5)
III. −5 − (−3)
A. I only
B. II only
C. III only
D. I and II
E. II and III
PS06555
Q-23: Point X lies on side BC of rectangle ABCD, which has length 12 and width 8. What is the area of triangular region AXD ?
A. 96
B. 48
C. 32
D. 24
E. 20
PS09983
A. 96
B. 48
C. 32
D. 24
E. 20
PS09983
Q-24: A grocer has 400 pounds of coffee in stock, 20 percent of which is decaffeinated. If the grocer buys another 100 pounds of coffee of which 60 percent is decaffeinated, what percent, by weight, of the grocer’s stock of coffee is decaffeinated?
A. 28%
B. 30%
C. 32%
D. 34%
E. 40%
PS07659
A. 28%
B. 30%
C. 32%
D. 34%
E. 40%
PS07659
Q-25: The toll T, in dollars, for a truck using a certain bridge is given by the formula T = 1.50 + 0.50( x − 2), where x is the number of axles on the truck. What is the toll for an 18-wheel truck that has 2 wheels on its front axle and 4 wheels on each of its other axles?
(A) $ 2.50
(B) $ 3.00
(C) $ 3.50
(D) $ 4.00
(E) $ 5.00
PS05129
(A) $ 2.50
(B) $ 3.00
(C) $ 3.50
(D) $ 4.00
(E) $ 5.00
PS05129
Q-26: For what value of x between − 4 and 4, inclusive, is the value of x^2 − 10x + 16 the greatest?
(A) − 4
(B) − 2
(C) 0
(D) 2
(E) 4
PS13917
(A) − 4
(B) − 2
(C) 0
(D) 2
(E) 4
PS13917
Q-27: If \(x = \frac{-5}{8}\) and \(y = \frac{-1}{2}\),what is the value of the expression \(-2x - y^2\)?
A. \(-\frac{3}{2}\)
B. ‒1
C. 1
D. \(\frac{3}{2}\)
E. \(\frac{7}{4}\)
PS15994
A. \(-\frac{3}{2}\)
B. ‒1
C. 1
D. \(\frac{3}{2}\)
E. \(\frac{7}{4}\)
PS15994
Q-28: If x-y= R and xy=S, then (x-2)(y+2)=
A. R+S-4
B. R+2S -4
C. 2R - S -4
D. 2R + S - 4
E. R + S
PS13686
A. R+S-4
B. R+2S -4
C. 2R - S -4
D. 2R + S - 4
E. R + S
PS13686
Q-29: For positive integers a and b, the remainder when a is divided by b is equal to the remainder when b is divided by a. Which of the following could be a value of ab ?
I. 24
II. 30
III. 36
A. II only
B. III only
C. I and II only
D. II and III only
E. I, II, and III
PS01466
I. 24
II. 30
III. 36
A. II only
B. III only
C. I and II only
D. II and III only
E. I, II, and III
PS01466
Q-30: List S consists of the positive integers that are multiples of 9 and are less than 100. What is the median of the integers in S ?
A. 36
B. 45
C. 49
D. 54
E. 63
PS01867
A. 36
B. 45
C. 49
D. 54
E. 63
PS01867
Q-31: A rope 20.6 meters long is cut into two pieces. If the length of one piece of rope is 2.8 meters shorter than the length of the other, what is the length, in meters, of the longer piece of rope?
A. 7.5
B. 8.9
C. 9.9
D. 10.3
E. 11.7
PS07380
A. 7.5
B. 8.9
C. 9.9
D. 10.3
E. 11.7
PS07380
Q-32: If x and y are integers and x − y is odd, which of the following must be true?
I. xy is even.
II. x^2 + y^2 is odd.
II. (x + y)^2 is even.
A. I only
B. II only
C. III only
D. I and II only
E. I, II, and III
PS01120
I. xy is even.
II. x^2 + y^2 is odd.
II. (x + y)^2 is even.
A. I only
B. II only
C. III only
D. I and II only
E. I, II, and III
PS01120
Q-33: On Monday, the opening price of a certain stock was $100 per share and its closing price was $110 per share. On Tuesday the closing price of the stock was 10 percent less than its closing price on Monday, and on Wednesday the closing price of the stock was 4 percent greater than its closing price on Tuesday. What was the approximate percent change in the price of the stock from its opening price on Monday to its closing price on Wednesday?
A. A decrease of 6%
B. A decrease of 4%
C. A decrease of 1%
D. An increase of 3%
E. An increase of 4%
PS00335
A. A decrease of 6%
B. A decrease of 4%
C. A decrease of 1%
D. An increase of 3%
E. An increase of 4%
PS00335
Q-34: 
In the rectangular coordinate system shown above, points O, P, and Q represent the sites of three proposed housing developments. If a fire station can be built at any point in the coordinate system, at which point would it be equidistant from all three developments?
A. (3,1)
B. (1,3)
C. (3,2)
D. (2,2)
E. (2,3)
PS05109
In the rectangular coordinate system shown above, points O, P, and Q represent the sites of three proposed housing developments. If a fire station can be built at any point in the coordinate system, at which point would it be equidistant from all three developments?
A. (3,1)
B. (1,3)
C. (3,2)
D. (2,2)
E. (2,3)
PS05109
Q-35: What is the perimeter, in meters, of a rectangular garden 6 meters wide that has the same area as a rectangular playground 16 meters long and 12 meters wide?
(A) 48
(B) 56
(C) 60
(D) 76
(E) 192
PS05008
(A) 48
(B) 56
(C) 60
(D) 76
(E) 192
PS05008
Q-36: 1 − 0.000001 =
A. (1.01)(0.99)
B. (1.11)(0.99)
C. (1.001)(0.999)
D. (1.111)(0.999)
E. (1.0101)(0.0909)
PS00918
A. (1.01)(0.99)
B. (1.11)(0.99)
C. (1.001)(0.999)
D. (1.111)(0.999)
E. (1.0101)(0.0909)
PS00918
Q-37: \(|−4|(|−20| − |5|) =\)
A. −100
B. −60
C. 60
D. 75
E. 100
PS04362
A. −100
B. −60
C. 60
D. 75
E. 100
PS04362
Q-38: Of the total amount that Jill spent on a shopping trip, excluding taxes, she spent 50 percent on clothing, 20 percent on food, and 30 percent on other items. If Jill paid a 4 percent tax on the clothing, no tax on the food, and an 8 percent tax on all other items, then the total tax that she paid was what percent of the total amount that she spent, excluding taxes?
A. 2.8%
B. 3.6%
C. 4.4%
D. 5.2%
E. 6.0%
PS12934
A. 2.8%
B. 3.6%
C. 4.4%
D. 5.2%
E. 6.0%
PS12934
Q-39: How many integers x satisfy both \(2 < x \leq 4\) and \(0 \leq x \leq 3\) ?
A. 5
B. 4
C. 3
D. 2
E. 1
PS15469
A. 5
B. 4
C. 3
D. 2
E. 1
PS15469
Q-40: At the opening of a trading day at a certain stock exchange, the price per share of stock ABC was $120. If the price per share of stock ABC was $125 at the closing of the day, what was the approximate percent increase in the price per share of stock ABC for that day?
A. 10%
B. 4%
C. 2%
D. 1%
E. -2%
PS09322
A. 10%
B. 4%
C. 2%
D. 1%
E. -2%
PS09322
Q-41: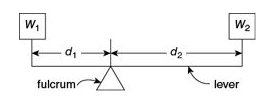 
As shown in the diagram above, a lever resting on a fulcrum has weights of w1 pounds and w2 pounds, located d1 feet and d2 feet from the fulcrum. The lever is balanced and \(w_1d_1=w_2d_2\). Suppose w1 is 50 pounds and w2 is 30 pounds. If d1 is 4 feet less than d2, what is d2, in feet?
A. 1.5
B. 2.5
C. 6
D. 10
E. 20
PS14237
As shown in the diagram above, a lever resting on a fulcrum has weights of w1 pounds and w2 pounds, located d1 feet and d2 feet from the fulcrum. The lever is balanced and \(w_1d_1=w_2d_2\). Suppose w1 is 50 pounds and w2 is 30 pounds. If d1 is 4 feet less than d2, what is d2, in feet?
A. 1.5
B. 2.5
C. 6
D. 10
E. 20
PS14237
Q-42: If r and s are positive integers such that (2^r)(4^s) = 16, then 2r + s =
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
PS01650
(A) 2
(B) 3
(C) 4
(D) 5
(E) 6
PS01650
Q-43: Three people each contributed x dollars toward the purchase of a car. They then bought the car for y dollars, an amount less than the total number of dollars contributed. If the excess amount is to be refunded to the three people in equal amounts, each person should receive a refund of how many dollars?
A. \(\frac{3x-y}{3}\)
B.\(\frac{x-y}{3}\)
C.\(\frac{x-3y}{3}\)
D.\(\frac{y-3x}{3}\)
E. 3(x-y)
PS06726
A. \(\frac{3x-y}{3}\)
B.\(\frac{x-y}{3}\)
C.\(\frac{x-3y}{3}\)
D.\(\frac{y-3x}{3}\)
E. 3(x-y)
PS06726
Q-44: Last week Jack worked 70 hours and earned $ 1,260. If he earned his regular hourly wage for the first 40 hours worked, 3/2 times his regular hourly wage for the next 20 hours worked, and 2 times his regular hourly wage for the remaining 10 hours worked, what was his regular hourly wage?
A. $ 7.00
B. $ 14.00
C. $ 18.00
D. $ 22.00
E. $ 31.50
PS07080
A. $ 7.00
B. $ 14.00
C. $ 18.00
D. $ 22.00
E. $ 31.50
PS07080
Q-45: If a and b are positive integers and \((2^a)^b = 2^3\), what is the value of \(2^a*2^b\)?
A) 6
B) 8
C) 16
D) 32
E) 64
PS13426
A) 6
B) 8
C) 16
D) 32
E) 64
PS13426
Q-46: Five machines at a certain factory operate at the same constant rate. If four of these machines, operating simultaneously, take 30 hours to fill a certain production order, how many fewer hours does it take all five machines, operating simultaneously, to fill the same production order?
(A) 3
(B) 5
(C) 6
(D) 16
(E) 24
PS01099
(A) 3
(B) 5
(C) 6
(D) 16
(E) 24
PS01099
Q-47: A certain toll station on a highway has 7 tollbooths, and each tollbooth collects $0.75 from each vehicle that passes it. From 6 o'clock yesterday morning to 12 o'clock midnight, vehicles passed each of the tollbooths at the average rate of 4 vehicles per minute. Approximately how much money did the toll station collect during that time period?
A. $1,500
B. $3,000
C. $11,500
D. $23,000
E. $30,000
PS01443
A. $1,500
B. $3,000
C. $11,500
D. $23,000
E. $30,000
PS01443
Q-48: How many integers between 1 and 16, inclusive, have exactly 3 different positive integer factors? (Note: 6 is NOT such an integer because 6 has 4 different positive integer factors: 1, 2, 3, and 6.)
A. 1
B. 2
C. 3
D. 4
E. 5
PS13829
A. 1
B. 2
C. 3
D. 4
E. 5
PS13829
Q-49: Stephanie has 9/4 cups of milk on hand and makes 2 batches of cookies, using 2/3 cup of milk for each batch of cookies. Which of the following describes the amount of milk remaining after she makes the cookies?
A. Less then \(\frac{1}{2}\) cup
B. Between\(\frac{1}{2}\)cup and \(\frac{3}{4}\)cup
C. Between \(\frac{3}{4}\)cup and 1 cup
D. Between 1 cup and\(\frac{3}{2}\) cups
E. More than \(\frac{3}{2}\) cups
PS14063
A. Less then \(\frac{1}{2}\) cup
B. Between\(\frac{1}{2}\)cup and \(\frac{3}{4}\)cup
C. Between \(\frac{3}{4}\)cup and 1 cup
D. Between 1 cup and\(\frac{3}{2}\) cups
E. More than \(\frac{3}{2}\) cups
PS14063
Q-50: The expression n! is defined as the product of the integers from 1 through n. If p is the product of the integers from 100 through 299 and q is the product of the integers from 200 through 299, which of the following is equal to p/q?
A. 99!
B. 199!
C. 199!/99!
D. 299!/99!
E. 299!/199!
PS01656
A. 99!
B. 199!
C. 199!/99!
D. 299!/99!
E. 299!/199!
PS01656
09 Jul 2020, 05:40
Kudos
Bookmarks
Hi Viewers,
Please watch the video below and like and share it with the ones who may really need it.
Please watch the video below and like and share it with the ones who may really need it.
22 Apr 2024, 19:31
Kudos
Bookmarks
Hello from the GMAT Club BumpBot!
Thanks to another GMAT Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).
Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.
Thanks to another GMAT Club member, I have just discovered this valuable topic, yet it had no discussion for over a year. I am now bumping it up - doing my job. I think you may find it valuable (esp those replies with Kudos).
Want to see all other topics I dig out? Follow me (click follow button on profile). You will receive a summary of all topics I bump in your profile area as well as via email.
