Forum Home > GMAT > Quantitative > Problem Solving (PS)
Events & Promotions
|
|
GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
Dec 1608:00 AM PST
-11:59 PM PST
GMAT Club 12 Days of Christmas is a 4th Annual GMAT Club Winter Competition based on solving questions. This is the Winter GMAT competition on GMAT Club with an amazing opportunity to win over $40,000 worth of prizes!
Dec 1511:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease.- Dec 17
09:00 AM PST
-10:00 AM PST
Join Manhattan Prep instructor Whitney Garner for a fun—and thorough—review of logic-based (non-math) problems, with a particular emphasis on Data Sufficiency and Two-Parts. - Dec 18
10:00 AM PST
-11:00 AM PST
Here is the essential guide to securing scholarships as an MBA student! In this video, we explore the various types of scholarships available, including need-based and merit-based options. - Dec 21
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment
09 Aug 2013, 14:10
Kudos
Bookmarks
C
Be sure to select an answer first to save it in the Error Log before revealing the correct answer (OA)!
Difficulty:
45%
(medium)
Question Stats:
56% (01:16) correct
44%
(00:59)
wrong
based on 295
sessions
History
Date
Time
Result
Not Attempted Yet
If each student gets at least one pencil in the exam hall, what is the probability that a student gets exactly one pencil in the exam hall?
(1) 110 students are expected to get at least one pencil.
(2) 60 students are expected to get at least two pencils.
(1) 110 students are expected to get at least one pencil.
(2) 60 students are expected to get at least two pencils.
st1 implies there are 110 students in the exam hall and everyone of them will get exactly one pencil.
but its not sufficient.
st2 tells, 60 students are expected to get at least two pencils. this not sufficient alone.
Now from both statements,
110 = exactly one + more than one
or 110 = exactly one + 60
or, exactly one = 50 .
so the probability of getting exactly one = 50/110 = 5/11 ,
so Answer (C)
but its not sufficient.
st2 tells, 60 students are expected to get at least two pencils. this not sufficient alone.
Now from both statements,
110 = exactly one + more than one
or 110 = exactly one + 60
or, exactly one = 50 .
so the probability of getting exactly one = 50/110 = 5/11 ,
so Answer (C)
10 Aug 2013, 20:05
Kudos
Bookmarks
x: Number of students get at least 1 pencil
a: Number of students get exactly 1 pencil
b: Number of students get more than 1 pencil
x= a + b
to find the probability that a student gets exactly one pencil, we need to know the number of student get exactly 1 pencil and the number of student get at least 1 pencil.
1. 110 students are expected to get at least one pencil: x=a + b = 110 --> insufficient
2. 60 students are expected to get at least two pencils or the number of student get more than 1 pencil b = 60 --> insufficient.
(1) + (2): we have: x = a + b = 110 and b = 60 => a=50
The probability that a student gets exactly 1 pencil is: 50/110 = 5/11 --> sufficient
The answer is C
1.
a: Number of students get exactly 1 pencil
b: Number of students get more than 1 pencil
x= a + b
to find the probability that a student gets exactly one pencil, we need to know the number of student get exactly 1 pencil and the number of student get at least 1 pencil.
1. 110 students are expected to get at least one pencil: x=a + b = 110 --> insufficient
2. 60 students are expected to get at least two pencils or the number of student get more than 1 pencil b = 60 --> insufficient.
(1) + (2): we have: x = a + b = 110 and b = 60 => a=50
The probability that a student gets exactly 1 pencil is: 50/110 = 5/11 --> sufficient
The answer is C
1.
11 Aug 2013, 01:12
Kudos
Bookmarks
Asifpirlo
if each student gets at least one pencil in the exam hall, what is the probability that a student gets exactly one pencil in the exam hall?
(1) 110 students are expected to get at least one pencil
(2) 60 students are expected to get at least two pencils
(1) 110 students are expected to get at least one pencil
(2) 60 students are expected to get at least two pencils
st1 implies there are 110 students in the exam hall and everyone of them will get exactly one pencil.
but its not sufficient.
st2 tells, 60 students are expected to get at least two pencils. this not sufficient alone.
Now from both statements,
110 = exactly one + more than one
or 110 = exactly one + 60
or, exactly one = 50 .
so the probability of getting exactly one = 50/110 = 5/11 ,
so Answer (C)
but its not sufficient.
st2 tells, 60 students are expected to get at least two pencils. this not sufficient alone.
Now from both statements,
110 = exactly one + more than one
or 110 = exactly one + 60
or, exactly one = 50 .
so the probability of getting exactly one = 50/110 = 5/11 ,
so Answer (C)
Each student gets one pencil . and 110 students got one pencil. There are 110 students in the exam hall.
Statement A:- 110 students gets atleast one pencil in the exam hall. With this we can only get the number of students in the exam hall.But not the number of students who got exactly one pencil. So A and D are out
Statement B:- 60 students are expected to get atleast two pencils in the exam hall. With this statement ALONE we will not be able to get the number of students who got exactly two pencils in the exam hall. So B is out.
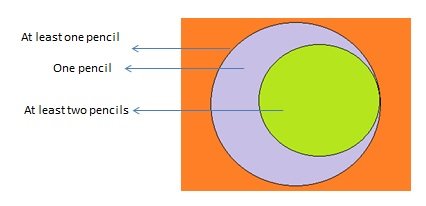
Both statements combined. we get that 110 students get atleast one pencil. and 60 students get atleast two pencils. Refer to the diagram below
Attachment:
set.jpg [ 17.47 KiB | Viewed 4540 times ]
So the number of students who got exactly one pencil is the middle portion. ie 110 - 60 = 50. So the answer is C
