In a certain department of ABC business school, there are either accou

Method 1:

From the statements, it should be clear that we need both statements to try and solve it. Individual statements offer too little information.

Let the total number of professors be \(3k\)
Number of accounting professors = \(2/3 * 3k = 2k\)
Number of financial professors = \(3k - 2k = k\)

Statement 1: Finance professors who do outside consulting = \(k/3\)
=> Finance professors who do not do outside consulting = Number of Finance professors - Finance professors who do outside consulting
\(= k - k/3 = 2k/3\)

Statement 2: Accounting professors who do outside consulting : Finance professors who do outside consulting = \(3 : 4\)
=> Accounting professors who do outside consulting = \(3/4\) * Finance professors who do outside consulting = \(3/4 * k/3 = k/4\)
=> Accounting professors who do not do outside consulting
= Number of Accounting professors - Accounting professors who do outside consulting
\(= 2k - k/4 = 7k/4\)

Thus, we have: ratio of the total number of professors that do outside consulting to the total number of professors that don't do outside consulting
\(= (k/3 + k/4) : (2k/3 + 7k/4)\)
= 7 : 29


Alternate approach: Using a Venn-diagram, the solution becomes kind of complicated:

According to the question, we know that:
An accounting professor doesn't teach finance and vice-versa; i.e. there is no professor who teaches both finance and accounting.
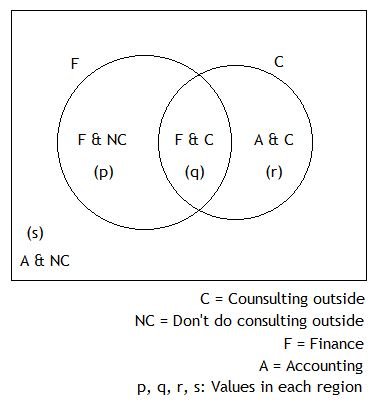
Thus, we can use a 2-Venn diagram with one representing the finance professors and the other representing the professors who participate in consulting outside.

The diagram is shown below:

We need to determine the ratio of the total number of professors that do outside consulting to the total number of professors that don't do outside consulting, i.e. \((q + r) : (p + s)\)

Since 2/3 of the professors are accounting professors (i.e. 1/3 of the professors are finance professors), we have:
Ratio of accounting professors to finance professors = 2 : 1
\(=> (r + s) : (p + q) = 2 : 1\) ... (i)

From Statement 1: 1/3 of the finance professors do outside consulting
\(=> q = (p + q)/3 => p = 2q\) ... (ii)

Even after using (i), we cannot determine the value of \((q + r) : (p + s)\) - Insufficient


From Statement 2: The ratio of the number of accounting professors that do outside consulting to the number of finance professors that do outside consulting is 3:4
\(=> r : q = 3 : 4\)
\(=> r = 3q/4\) ... (iii)

Even after using (i), we cannot determine the value of \((q + r) : (p + s)\) - Insufficient

Combining the statements:

From (i): \(=> (r + s) : (p + q) = 2 : 1\)
\(=> (r + s) = 2(p + q)\)

Using \(p = 2q\) and \(r = 3q/4\):

\(=> (3q/4 + s) = 2(2q + q)\)
\(=> s = 21q/4\)

Thus, we have:

\((q + r) : (p + s) = (q + 3q/4) : (2q + 21q/4) = 7 : 29\) - Sufficient

Answer C