Events & Promotions
|
|

GMAT Club Daily Prep
Thank you for using the timer - this advanced tool can estimate your performance and suggest more practice questions. We have subscribed you to Daily Prep Questions via email.
Customized
for You
Track
Your Progress
Practice
Pays
Not interested in getting valuable practice questions and articles delivered to your email? No problem, unsubscribe here.
- Nov 19
12:30 PM EST
-01:30 PM EST
Learn how Keshav, a Chartered Accountant, scored an impressive 705 on GMAT in just 30 days with GMATWhiz's expert guidance. In this video, he shares preparation tips and strategies that worked for him, including the mock, time management, and more - Nov 20
07:30 AM PST
-08:30 AM PST
Learn what truly sets the UC Riverside MBA apart and how it helps in your professional growth - Nov 20
01:30 PM EST
-02:30 PM IST
Learn how Kamakshi achieved a GMAT 675 with an impressive 96th %ile in Data Insights. Discover the unique methods and exam strategies that helped her excel in DI along with other sections for a balanced and high score. - Nov 22
11:00 AM IST
-01:00 PM IST
Do RC/MSR passages scare you? e-GMAT is conducting a masterclass to help you learn – Learn effective reading strategies Tackle difficult RC & MSR with confidence Excel in timed test environment - Nov 23
11:00 AM IST
-01:00 PM IST
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease. - Nov 24
07:00 PM PST
-08:00 PM PST
Full-length FE mock with insightful analytics, weakness diagnosis, and video explanations! - Nov 25
10:00 AM EST
-11:00 AM EST
Prefer video-based learning? The Target Test Prep OnDemand course is a one-of-a-kind video masterclass featuring 400 hours of lecture-style teaching by Scott Woodbury-Stewart, founder of Target Test Prep and one of the most accomplished GMAT instructors.
Originally posted by EgmatQuantExpert on 04 Apr 2018, 07:03.
Last edited by EgmatQuantExpert on 08 Aug 2018, 06:12, edited 11 times in total.
Last edited by EgmatQuantExpert on 08 Aug 2018, 06:12, edited 11 times in total.
Kudos
Bookmarks
Added the PDF of the article at the end of the post! 
Why should you read this article?
If the answer to any of the above questions is yes, then in this e-GMAT article you will learn how to get rid of the confusion by using “AND” & “OR” on these questions.
What will you learn from this article?
In this e-GMAT article, we will:
When to Add – Usage of the keyword “OR”
While solving any P and C question, the most frequent confusion that students have is: “Do I need to add up all the cases or do I need to multiply all the cases?”
Let’s understand what I am trying to say with the help of two questions!
Look at these two situations. In both these cases, the numbers are the same. The only difference is that Amy will choose either shoes OR sandals to wear and in the second case Joe is going to choose both a shirt AND a trouser.
Let us focus on Amy’s situation first, and then we will come to Joe.
Assuming that she has red, green, and black shoes, and she has brown and blue sandals, let us list down all the possible options that she has.
Notice how we have used the word OR after each and every case. The OR here emphasizes on the fact that Amy does not have the option to wear two different kinds of things at the same time! She needs to choose only 1 of these.
Thus, the answer, in this case, will be 5.
Now let us use the keyword approach (OR) to solve this question easily!
Keyword Approach by e-GMAT
Look at the question once again:
Whenever we have a situation in which two events cannot occur simultaneously, we simply add all the cases. Thus, in this case, we will say:
Takeaway by e-GMAT experts
When to Multiply – Usage of Keyword “AND”
Now let us look at Joe’s case.
Assuming that he has red, green, and a black shirt, and he has brown and blue trousers, let us list down all the possible options that he has.
Notice how I have used the word AND after each and every case.
The AND here emphasizes on the fact that Joe has to wear both shirt AND trousers at the same time!
We cannot imagine a scenario, where he wears just a shirt OR just a trouser.
From the above cases, we can see that he has 6 different options for wearing a shirt and a trouser.
Now let use the keyword approach (AND) to solve this question easily! ?
Let’s use the Keyword “AND”
Look at the question once again:
Whenever we have a situation in which two events can happen simultaneously, we simply “multiply” all the cases.
Thus, in this case, we can say:
Takeaway by e-GMAT experts
What to do when AND or OR keyword is not present?
Now, there could be a situation when the word AND or OR is not explicitly mentioned in the question.
What should we do then? Let us understand this with the help of 3 examples:
e-GMAT Example 1
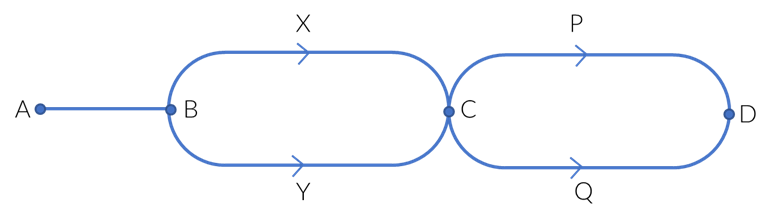
Q-In the above diagram, in how many ways can you go from Point A to point D?
Solution
In the question and diagram, you can see that there is no mention of the word AND or OR, so what should we do?
• Thus, total cases possible are = 1 x 2 x 2 = 4 ways
Let us increase the difficulty a bit and figure out how to solve the following question.
e-GMAT Example 2
Q-How many 3 digits even numbers can be created using the digits 1,2,3, 4 and 5 without repetition of digits?
Solution
This question does not mention the keywords, AND or OR.
Hence, we will try to figure out what the question is asking.
Any 3-digit number can be represented as:

Let us come to the last question of this e-GMAT article.
e-GMAT Example 3
Q- A committee of 2 members is to be formed from a panel of 4 male and 3 female members of a club.
In how many ways can the committee be formed?
Solution
You should now start thinking a step ahead to find the use of AND-/OR in such problems.
Let us find out how we can form the committee of 2 members in the above question.
Let us find in how many we can select 2 males, 2 females and 1 male and 1 female.
Thus, total ways= 4c2+ 3c2+ 4c1*3c1 = 6+3+4*3=21
Thus, the committee can be formed in 21 ways.
Takeaway from this article
Get access to more amazing content by signing up for a comprehensive free trial from e-GMAT.
Upcoming e-GMAT articles on Permutation & Combination
This article is one of a series of e-GMAT articles that we are going to write on Permutation and Combination.
Stay tuned….
Learn when to “Add” and “Multiply” in Permutation & Combination questions
Why should you read this article?
- • Are you someone who is confused whether to add or multiply the cases while solving permutation and combination questions?
• Do you often get questions incorrect simply because you added entities instead of multiplying them?
If the answer to any of the above questions is yes, then in this e-GMAT article you will learn how to get rid of the confusion by using “AND” & “OR” on these questions.
What will you learn from this article?
In this e-GMAT article, we will:
- 1. Dive into the details of the application of “AND” & “OR” in permutation and combination.
2. Discuss the attributes that AND – OR present through a few GMAT like questions
3. Help you to solidify the understanding of the above two keywords and at the end of the article, we will also provide you a few practice questions to test your understanding.
When to Add – Usage of the keyword “OR”
While solving any P and C question, the most frequent confusion that students have is: “Do I need to add up all the cases or do I need to multiply all the cases?”
Let’s understand what I am trying to say with the help of two questions!
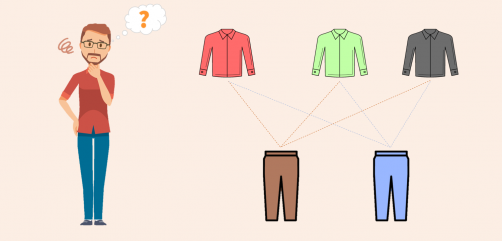
- • Amy has 3 different types of shoes and 2 different types of sandals. Whenever she goes out, she likes to wear either a shoe or a sandal. In how many ways can she decide what to wear?
• Joe has 3 different types of shirts and 2 different types of trousers. Whenever he goes out, he likes to wear a shirt and a trouser. In how many ways can he decide what to wear?
Look at these two situations. In both these cases, the numbers are the same. The only difference is that Amy will choose either shoes OR sandals to wear and in the second case Joe is going to choose both a shirt AND a trouser.
Let us focus on Amy’s situation first, and then we will come to Joe.
Assuming that she has red, green, and black shoes, and she has brown and blue sandals, let us list down all the possible options that she has.
- 1. She can wear Red Shoes OR
2. She can wear Green shoes OR
3. She can wear Black Shoes OR
4. She can wear Brown Sandals OR
5. She can wear Blue Sandals
Notice how we have used the word OR after each and every case. The OR here emphasizes on the fact that Amy does not have the option to wear two different kinds of things at the same time! She needs to choose only 1 of these.
Thus, the answer, in this case, will be 5.
Now let us use the keyword approach (OR) to solve this question easily!
Keyword Approach by e-GMAT
Look at the question once again:
- • Amy has 3 different types of shoes and 2 different types of sandals. Whenever she goes out, she likes to wear either a shoe OR a sandal. In how many ways can she decide what to wear?
- o Notice the OR that I have highlighted in this question.
- • Whenever you read a question, look for the keyword OR or AND. While looking for the keyword, focus on what we need to find out.
- o In this case, we need to find the number of ways in which she can wear a shoe OR a sandal.
o Since the word OR is used here, we can conclude that both the events cannot happen together.
- By event I mean, Amy cannot wear Shoe, and Sandal together.
Whenever we have a situation in which two events cannot occur simultaneously, we simply add all the cases. Thus, in this case, we will say:
- •Total possible cases for Amy = She will wear shoes OR she will wear Sandals
- oNumber of ways she can wear shoes = 3
oNumber of ways she can wear Sandals = 2
Takeaway by e-GMAT experts
- 1- Whenever we come across a situation involving 2 or more events, and occurrence of one event does not affect the occurrence of the other event, i.e., both of the events cannot occur simultaneously, then, in that case, we will simply add up all the events!
2- Look for the word OR in the question while figuring out what you need to find out and if OR is present then that means you need to add up the events.
When to Multiply – Usage of Keyword “AND”
Now let us look at Joe’s case.
Assuming that he has red, green, and a black shirt, and he has brown and blue trousers, let us list down all the possible options that he has.
- 1. He can wear Red Shirt AND Brown Trousers
2. He can wear Red Shirt AND Blue Trousers
3. He can wear Green shirt AND Brown Trousers
4. He can wear Green shirt AND Blue Trousers
5. He can wear Black shirt AND Brown Trousers
6. He can wear Black shirt AND Blue Trousers
Notice how I have used the word AND after each and every case.
The AND here emphasizes on the fact that Joe has to wear both shirt AND trousers at the same time!
We cannot imagine a scenario, where he wears just a shirt OR just a trouser.
From the above cases, we can see that he has 6 different options for wearing a shirt and a trouser.
Now let use the keyword approach (AND) to solve this question easily! ?
Let’s use the Keyword “AND”
Look at the question once again:
- • Joe has 3 different types of shirts and 2 different types of trousers. Whenever he goes out, he likes to wear a shirt AND a trouser. In how many ways can he decide what to wear?
- o Notice the AND that I have highlighted in this question.
- • In this case also focus on what we need to find out.
- o In this case, we need to find the number of ways he can wear a shirt AND a trouser.
o Since the word AND is used here, we can conclude that both the events need to happen together.
- Which means he needs to wear the shirt and trouser together.
Whenever we have a situation in which two events can happen simultaneously, we simply “multiply” all the cases.
Thus, in this case, we can say:
- •Total possible cases for Joe = He will wear a Shirt AND he will wear Trousers
- oNumber of ways he can wear a shirt = 3 ( Red OR Green OR Black) [ Keyword OR: hence addition]
oNumber of ways he can wear trousers = 2 (Blue OR Brown)
•Therefore, total possible cases = 3 AND 2 = 3 x 2 = 6
Takeaway by e-GMAT experts
- 1- Please remember that whenever we come across a situation involving 2 or more events and each event can happen simultaneously, i.e., event 1, event 2, event 3 and so on, all can happen simultaneously.
Then, in that case, we will simply MULTIPLY up all the events!
2- Look for the word AND in the question while figuring out what you need to find out, and if AND is present, then that means you need to multiply the events.
What to do when AND or OR keyword is not present?
Now, there could be a situation when the word AND or OR is not explicitly mentioned in the question.
What should we do then? Let us understand this with the help of 3 examples:
e-GMAT Example 1

Q-In the above diagram, in how many ways can you go from Point A to point D?
Solution
In the question and diagram, you can see that there is no mention of the word AND or OR, so what should we do?
- • Well, we will simply look at the each and every end point and figure out what are we exactly doing.
• So, think, in how many ways can we go from point A to B?
- o We can go in one way, right?
o So, let us just write A -> B : 1 way
- • Now, when we want to go from B to C, we can go via X OR Y.
- o Notice how we are using the word OR here.
o We know that we cannot simultaneously go via both the routes. And thus, we need to use the word OR here.
- Thus, total number of ways to go from B to C = 2
B ->X ->C OR B->Y->C = 2 ways
- • Lastly, we want to go to our final destination D, we can go via P OR Q
- o In this case also, we are using the word OR.
o Hence, we will simply ADD all the cases and get C->D = 2 ways.
- • So, now we know that we can go from A to B in 1 way, then from B to C in 2 ways and from C to D in 2 ways.
- o Now, ask yourself, should we add these cases or multiply?
o Can we reach from A to D by going through A to B or B to C or C to D?
- No, we cannot, right?
We need to go from A to B AND then from B to C AND finally from C to D to reach our destination.
• Thus, total cases possible are = 1 x 2 x 2 = 4 ways
Let us increase the difficulty a bit and figure out how to solve the following question.
e-GMAT Example 2
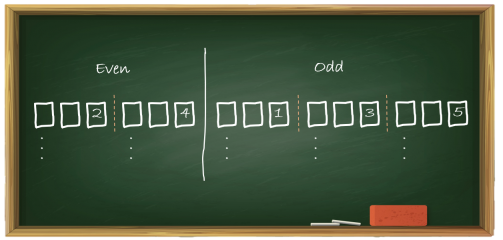
Q-How many 3 digits even numbers can be created using the digits 1,2,3, 4 and 5 without repetition of digits?
Solution
This question does not mention the keywords, AND or OR.
Hence, we will try to figure out what the question is asking.
Any 3-digit number can be represented as:

- • We have to make a 3-digit number.
- o Now think, can we make a three-digit number by just filling the Units place OR the tens place OR the hundreds place?
- No, we cannot, Right?
o Notice, we used the keyword AND here. Hence, we will multiply all the cases
- Thus,

- • We have to form a 3 digit even number.
- o Hence, the units digit of the number must be even.
o Among the given digits: 1, 2, 3, 4, and 5, the units can be filled with 2 digits.
- Either 2 OR 4.
Can you see the usage of the keyword OR here?
- • Now, we have filled the units digit to take care of the even nature of the number.
- o We have 4 digits remaining – 1 even and 3 odd.
o The tens place can be filled with either 1 OR 3 OR 5 OR the remaining number between (2/4).
- Thus, total ways to fill tens place= 4 ways.
- • Now, we only have to fill the last digit and we have 3 digits remaining.
- o Are you now able to visualise that we will use OR to select 1 among the 3 digits?
- We can select either the 1st remaining digit OR the 2nd remaining digit OR the 3rd remaining digit
We used the keyword OR here. Hence, we will add the cases.
- • Thus, total ways to fill tens place= 3 ways.
- • As discussed, we need to multiply all these 3 individual cases to get the total number of ways in which the number can be formed.
- o Hence total ways= 3*4*2=24 ways
Let us come to the last question of this e-GMAT article.
e-GMAT Example 3
Q- A committee of 2 members is to be formed from a panel of 4 male and 3 female members of a club.
In how many ways can the committee be formed?
Solution
You should now start thinking a step ahead to find the use of AND-/OR in such problems.
Let us find out how we can form the committee of 2 members in the above question.
- • We can select either 2 males OR 2 females OR 1 male AND 1 female to form the committee.
- o Look for the keywords- AND and OR in the above statement.
o Now it is easy, we know that we add the number of cases when we have an OR, and, we multiply the cases when we have an AND.
o Total ways= ways to select 2 males + ways to select 2 females + ways to select 1 male * ways to select 1 female
Let us find in how many we can select 2 males, 2 females and 1 male and 1 female.
- • We have 4 males:
- o We can select 2 males from 4 males in 4c2 ways and,
o We can select 1 male from 4 males in 4c1 ways.
- • We have 3 females:
- o We can select 2 females in 3c2 ways and,
o We can select 1 females in 3c1 ways.
Thus, total ways= 4c2+ 3c2+ 4c1*3c1 = 6+3+4*3=21
Thus, the committee can be formed in 21 ways.
Takeaway from this article
- 1. Specific keywords can be the X-factor in solving PNC questions. You can trust them, but at the same time apply common sense just to be sure you are on the right path.
2. Always try to figure out after reading the question whether the events are dependent or independent. Making this inference will help you solve the question more efficiently.
3. Whenever we have a situation where OR is involved, please ADD up all the events.
4. Whenever we have a situation where AND is involved, please MULTIPLY all the events,
5. Whenever the keyword is not available, always try to jot down all the events first and then decide whether you need them together or independently.
Get access to more amazing content by signing up for a comprehensive free trial from e-GMAT.
Upcoming e-GMAT articles on Permutation & Combination
This article is one of a series of e-GMAT articles that we are going to write on Permutation and Combination.
- • We have two more articles coming up in the next 10 days, in which we are going to discuss the following aspects:
- o In article 2, you will learn a sure shot way to identify when to apply selection and when to apply both, selection, and arrangement.
o In article 3, you will learn how to avoid Double Counting: A Common Mistake made by a majority of student!
Stay tuned….
Attachments
![]() Permutation_AND_OR.pdf [569.42 KiB]
Permutation_AND_OR.pdf [569.42 KiB]
Downloaded 638 times
Originally posted by EgmatQuantExpert on 04 Apr 2018, 07:04.
Last edited by EgmatQuantExpert on 13 Aug 2018, 07:19, edited 2 times in total.
Last edited by EgmatQuantExpert on 13 Aug 2018, 07:19, edited 2 times in total.
Kudos
Bookmarks
Hey Everyone,
Here is a list of questions specifically designed to help you apply the learnings from this article.
Exercise Questions
Question 1
Question 2
Question 3
Question 4
Question 5
Detailed solutions will be posted soon.
Happy Learning!
General Discussion
Kudos
Bookmarks
Thanks so much, this is very helpful.
Sent from my iPhone using GMAT Club Forum
Sent from my iPhone using GMAT Club Forum